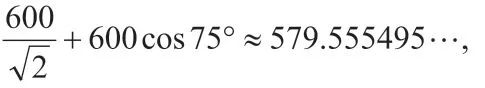哪个答案更准确——兼谈一道中考题的解法

安徽省南陵县籍山镇新建初级中学 章正平

现实世界中，有许多数只能近似表示，不管你容许还是不容许，因为这些数根本就不知道准确值，比如人的身高、体重等。人们说计算机计算准确，但也不能算出人的绝对精确重量，除了那些能够用精确值表达的数。对于很多数值，我们不能做到绝对准确，但可力求相对准确，如果需要的话，可以设法使数学模型更合理些，测量仪器精确度更高些，计算机更先进些。那么计算机是怎样计算的呢？计算机只会加减乘除等基本运算及简单的逻辑运算，例如要算的值，可以展成级数运算：应该算到第几项与具体精确度有关，还与计算机本身的功能有关，一般来说，项数越多，精确度越高。如果本身x 的值不准确而要求的精确度很高，就毫无意义了，还有用迭代的方法，比如算可用迭代公式先人为地给定一个y,然后代入公式求得y1,再继续代入求得y2……若迭代次数越多，则越准确，一直到指定的精度为止。

但求近似数远不是以上讲的那么简单，我们看一个例子：有一半径为的圆柱和两个互相垂直又与之相切的平面，试求一个与圆柱及这两个平面都相切的球的体积。

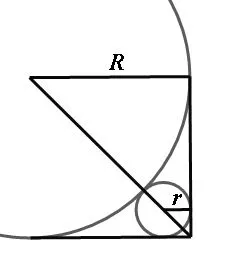
图1

1.4 1 0.004096 2 0.008

3 1 4images/BZ_44_1823_1117_1840_1134.png0.005232 5images/BZ_44_1786_1228_1803_1245.png0.0051252 6images/BZ_44_1793_1340_1810_1357.png0.00507614

表中的六个x 值都不一样，有的差别很大，结论是第六种最好，第三种最不好，只有学了计算数学才会明白。

这种情况在去年安徽省数学中考试题中出现了，去年我被抽调批改中考数学卷，任务是批改17 题：如图2，游客在点A 处坐缆车出发，沿的路线到山顶处。假设和都是直线段，且AB=BD=600m的长。（参考数据：

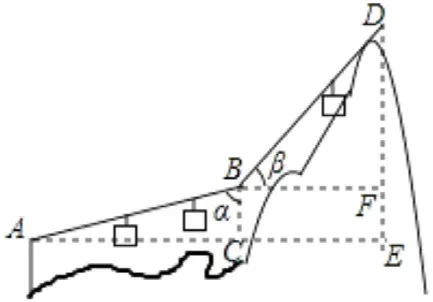
图2

这个题目非常简单，参考答案给的方法是：

但是在批改试卷过程中发现，许多同学不是这么解的，还有其他常见解法：