矩阵集极值的定义及其性质

刘庆怀， 张宝骥

(长春工业大学 数学与统计学院, 吉林 长春 130012)

0 引 言

矩阵集极值是研究矩阵值函数极值问题(Matrix Valued Function Extremum Problem, MVFE)的基础，而MVFE问题是矩阵优化的重要组成部分。矩阵优化可分为两类:一类是以矩阵为变量的优化问题，如半定规划、最低秩相关系数矩阵问题、特征值优化问题、锥约束优化问题等;另一类就是目标函数值为矩阵的MVFE问题，后者在算子方程、矩阵不等式、稀疏优化、约束矩阵方程、最小二乘问题等多个领域都有着重要的应用。近年来，矩阵集极值和MVFE问题受到越来越多的学者关注，H Mohebi[1]研究了对称的矩阵值函数连续性及其可微性；D F Sun等[2]讨论了矩阵值函数的半光滑性质及其应用。唐晓超[3]研究了矩阵值函数极小化问题的有效解及其性质；姚云飞等[4]讨论了在非负定矩阵偏序下的无约束MVFE问题，以及Banach空间中向量值的Bochner积分型的广义Jensen不等式；这些结果为矩阵集极值和MVFE问题的研究打下良好基础。由于向量集极值问题是矩阵集极值问题的特例，因此，关注抽象空间上的向量优化问题很有必要。到目前为止，在抽象空间上对包括极值优化问题在内的向量优化问题的研究已取得了相当丰硕的成果，尤其是在各种锥偏序关系或偏好关系下的标量化方法，以及锥有效解和拟弱有效解的存在性方面[5-8]。随着抽象空间中向量优化问题深入研究，以及矩阵值函数、矩阵理论与方法的不断发展[9-11]，为进一步研究矩阵集极值与MVFE问题提供理论基础和方法借鉴。

文中首先在锥序下给出矩阵集极值的S序有效阵与S序弱有效阵概念。其次，由半负定矩阵集诱导出的序关系界定了矩阵集的半负定有效阵与弱半负定有效阵。最后，通过加权的方法将矩阵集极值问题转化成向量集极值问题，定义了加权有效阵，利用矩阵的L0和L1范数给出了矩阵集的L0范数最优阵与L1范数最优阵。

1 矩阵集极值

文中所论述的矩阵集X为Rn×n中的非空闭集，其极值均为某种意义下的Pareto极小，Pareto极大可类似讨论。

1.1 S序有效阵与S弱序有效阵

定义1设S⊆Rn×n，S为非空闭凸集，并且

1)若A∈S,λ∈R+，则有λA∈S；

2)若A∈S,-A∈S，则有A=θ(θ为Rn×n中的零元素)。

此时则称S为一点式锥。

定义2设S⊆Rn×n为一点式锥，记So=intS。

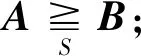
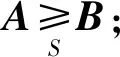
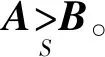
在上述序关系下，定义矩阵集X⊆Rn×n的极值。

定义3设A*∈X⊆Rn×n,

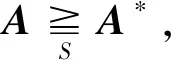
2)若不存在A∈X满足

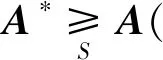
则称A*为X的S序有效阵(或S序弱有效阵)，并将X中的S序有效阵全体记作Rpa(X,S)(S序弱有效阵全体记作Rw(X,S))。

定理1

1)A*∈Rw(X,S)当且仅当X∩(A*-So)=Φ;

2)A*∈Rpa(X,S)当且仅当X∩(A*-So)={A*}。

证明

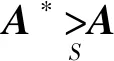
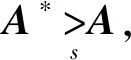
3)类似1)证明，可得结论2)成立。

由定义2、定义3易知下述推论成立。

推论1Rab(X,S)⊂Rpa(X,S)⊆Rw(X,S)。

1.2 半负定有效阵与弱半负定有效阵

在此给出由(半)负定矩阵诱导出的序关系。设S为Rn×n之中半负定矩阵所组成的集合，So为Rn×n之中负定矩阵所组成的集合。

定义4设A,B∈Rn×n,

1)若A-B∈S或B-A∈-S，则称A≤B或B≥A；

2)当A-B∈So或B-A∈-So，则称AA。

由上述定义易知，在Rn×n中，序关系“≥”满足:

1)反身性：∀A∈Rn×n，都有A≥A；

2)反对称性：∀A,B∈Rn×n，若A≥B且B≥A，则有A=B；

3)传递性：∀A,B,C∈Rn×n，若A≥B且B≥C，则有A≥C。

由此可知，在Rn×n中，“≥”是一偏序关系。

定理2设A,B∈Rn×n，则有:

1)A≥B当且仅当-B≥-A，A>B当且仅当-B>-A；

2)若A≥0且-A≥0，则A=0；

3)若A≥0且B≥0，则A+B≥0；

4)若A≥0且B>0，则A+B>0。

证明

1)由(半)正定矩阵的定义易得该结论。

2)由A≥0可知A的所有特征根皆非负，由-A≥0可知A的所有特征根皆非正，故A的所有特征根皆为零，故A正交相似于零矩阵，故A本身便是一个零矩阵。

3)由A≥0和B≥0可知AT=A，BT=B，而且对于任意的n维实向量α，皆有αTAα≥0，αTBα≥0，故(A+B)T=AT+BT=A+B，且∀α∈Rn，都有

αT(A+B)α=αTAα+αTBα≥0,

故A+B是一个半正定矩阵，即A+B≥0。

4)若A≥0且B>0，则和3)同理可得A+B>0。

在定义4所界定的偏序关系之下，给出矩阵集X⊆Rn×n半负定有效阵的概念。

定义5设A*∈X⊆Rn×n,

1)若∀A∈X都有A*-A∈S，便称A*为X的半负定绝对最优阵；

2)若不存在A∈X满足

A-A*∈S或A-A*∈So,

则称A*为X的半负定有效阵或半负定弱有效阵。

1.3 加权有效阵与范数最优阵

首先通过加权的方法将矩阵集极值问题转化成向量集极值问题。所以使用的序关系为向量集中的序关系(自然序)。其次利用矩阵的L0和L1范数定义矩阵集的L0范数最优阵与L1范数最优阵。

设A∈X⊆Rn×n，其中A=(A1,A2,…,An)，

k=1,2,…,n。

权向量

λ=(λ1,λ2,…,λn)T∈Λ+,

其中

Λ+={(λ1,λ2,…,λn)T|λk≥0,

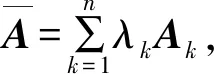
X,λ=(λ1,λ2,…,λn)T∈Λ+}。

下面用向量集中的坐标序来界定矩阵集X⊆Rn×n的极值概念。

则称A*为X的加权有效阵(或弱加权有效阵)。

设A∈X⊆Rn×n，记

矩阵A的L0范数定义为

‖A‖0≜{A中非零元素的个数}。

矩阵A的L1范数定义为

定义8设A*∈X，若对∀A∈X，都有

‖A*‖0≦‖A‖0,

则称A*为X的L0范数最优阵。

定义9设A*∈X，若对∀A∈X，都有

‖A*‖1≦‖A‖1,

则称A*为X的L1范数最优阵。

2 结 语

由于矩阵值函数极值问题的像集是矩阵集合，因此，文中所给出的矩阵集极值的定义为研究矩阵值函数极值奠定了基础，界定矩阵值函数极值的Pareto有效解是作者的后继工作。此外，应进一步研究非方阵的矩阵集极值问题，以及求解范数最优阵的方法。