例谈构造法在数学竞赛中的应用
湖北省武汉市武汉二中 齐韫哲
构造法在数学竞赛中经常用到,它即可以训练学生的数学思维,又可以化繁为简,经常可以起到事半功倍的好效果。运用构造法解题,先要认真分析题目,展开丰富的联想,从中发现可用构造法的因素,然后借助于与之相关的知识结构构造所求问题的具体形式,最后求解所构造的问题,并注意回到原来的问题中去加以说明或证明。下面结合实例分析说明常见的几种构造法在数学竞赛中的应用。
一、构造函数法
例1 已知x,y,z∈(0,1),求证:x(1-y)+y(1-z)+z(1-x)<1。(第15届俄罗斯数学竞赛题)
分析:此题的条件与结论都具有一定的轮换对称性,然而难以直接利用分类讨论法来证明,不妨利用构造法试试。
证明:构造关于x的一次函数 f(x)=(y+z-1)x+(yz-y-z+1)。
因为这里y,z∈(0,1),且有f(0)=yz-y-z+1=(y-1)(z-1)>0,
f(1)=(y+z-1)+(yz-y-z+1)=yz> 0,
又f(x)是一次函数,其图像是一条直线,所以有x∈(0,1)时,恒有 f(x) > 0,
即(y+z-1)x+(yz-y-z+1)>0, 整理得x(1-y)+y(1-z)+z(1-x) < 1。
二、构造方程法
例2 设实数a,b,c满足a2-bc-8a-7=0,b2+c2+bc-6a+6=0。求a的取值范围是多少。(1986年全国高中数学联赛题)
分析:通过观察题目,展开联想,发现可以用a来表示b+c和bc,所以可以构造以b,c为根的一元二次方程。然后利用根与系数的关系定理来求a的取值范围。
解:由已知得b+c=±(a-1),bc=a2-8a+7,所以构造关于x的一元二次方程得x2±(a-1)x+a2-8a+7=0。
因为b,c为该方程的两个实根,所以Δ=[±(a-1)]2-4(a2-8a+7)≥0,整理得a2-10a+9≤0,即1≤a≤9。
三、构造多项式法
例3 证明:对于同样的整数x和y,表达式2x+3y和9x+5y能同时被17整除。(首届IMO试题)
分析:要证明表达式2x+3y和9x+5y能同时被17整除,即要找到这两个表达式的线性组合的一个代数式,使它们的值是17的倍数即可。
证明:构造代数式9(2x+3y)-2(9x+5y),其值等于17y,能被17整除,结合2与9均与17互素,结论得证。
四、构造向量法
分析:柯西不等式在高中数学中有着较为广泛的应用,其定理本身有很多不同的证法,如构造一个二次函数,利用判别式法也不失为一种好的证法,但用构造向量法证明来得更简捷明了。
五、构造图形法
例5 若a,b,c,m,n,k>0,且有a+n=b+k=c+m=p,求证:ak+bm+cn<p2。(第26届全苏数学竞赛题)
分析:通过已知条件联想到构造一个边长为p的等边三角形,然后运用面积法来求证。
证明:构造一个边长为p的等边三角形ABC,如图。
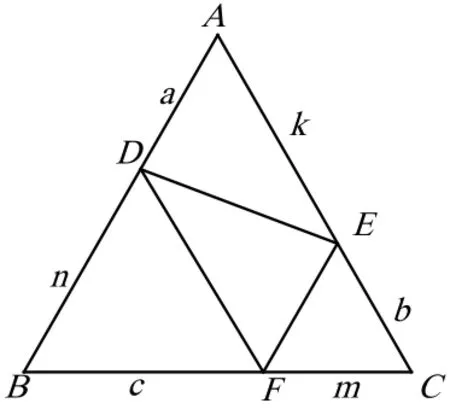
故有 ak+bm+cn<p2。
点评:以上结合例题列举了5种常见的构造法,由此可见这些方法在解题中往往可以起到化繁为简、事半功倍的效果,但是构造法往往比较难以掌握,需要平时仔细观察题目的已知条件与所求结论,从中找到知识结构的内在联系,日积月累。

