“有效”设问，“导学”课堂

浙江省宁波市鄞州区董玉娣中学 俞丽娜

数学学习并非是一个被动的接受过程，而应该是一个主动的建构过程，所以应该有效地让学生领悟到学习数学的方法和要领，启发学生积极创造，引导学生自己探索。那么作为教师要诱导学生去体验和探究，就要在教学情境中创设可实现的、有层次的有效问题来驱动学生不断进行探索。

在问题驱动下，学生实践探究活动，那么学生作为探究的主体，教师必须给予广阔的创作和探究的空间，让学生在充分的自主活动过程中不断体验、不断尝试、不断验证，从而开展探索和创新，做到真正地让学生“动”起来，积极主动地参与到数学探究活动中来。

一、开放式设问，发散思维

开放式设问指的是在实际教学中提供给学生一个个开放式的问题，从而创设一个开放式的课堂，在整个课堂教学过程中，弱化教师的主体地位，更多地发挥教师的主导作用，充分引导学生进行自主探究、自主思考、自主交流，在课堂中形成良好的互动模式，充分调动学生的积极性和主体地位。

例如，在探究“矩形折叠问题”这一专题课堂中，首先抛出一个开放式的问题：

（1）如图1，已知矩形纸片ABCD，若将矩形纸片沿EF折叠，使点A与点C重合，请说出尽可能多的结论，并说明理由。(不再添加其他辅助线)

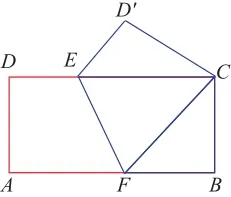
图1

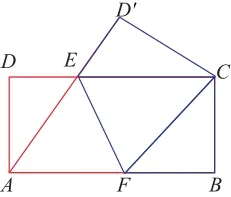
图2

学生通过观察，从边的等量关系、角的等量关系、三角形全等关系、面积的等量关系等诸多问题中，发散性地将矩形的性质全面而细致地进行了复习。紧接着，教师再提问：

（2）如图2，连接AE，你又能有什么新的结论？

通过这一开放性设问，引导学生发现更多边、角、三角形的等量关系，乃至涉及了菱形的性质与判定，培养了学生思考问题的全面性、严谨性，也为下面的探究做好铺垫。

（3）将矩形当中的三角形进行折叠（如图3），通过面积问题的计算不仅让学生对矩形的判定进行了回顾，也再次认识了菱形面积的两种计算方式，最后设问：若AB=4，BC=2，你能求出EF的长吗？

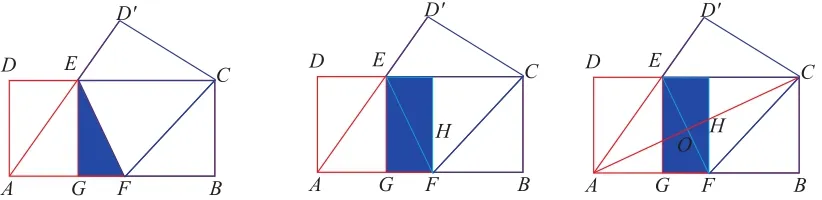
图3

在这节课的引入教学中，通过开放式的设问，引导学生的思维逐步从回顾——理解——解决问题，让学生被引导着感知如何解决矩形折叠问题中线段长度的求解方法，水到渠成。

二、“问题链”设问，引发探究

在课堂教学中，通过循序渐进的问题链，能促使学生去发现问题，并尝试解决问题，再到发现新的问题，从而获取新知，学会迁移新知，锻炼了能力的同时强化了学生的自我思考意识。

例如，在反比例函数的图像及性质第二课时的教学时，教师设置如下“问题链”：

（1）求此反比例函数的解析式；画出图像，判断点B（-4，-1）是否在此函数图像上。

（2）根据图像，若y＞1，则确定x的取值范围；若x＜1，则确定y的取值范围。

（3）若点（x1，y1)，（x2，y2)，（x3，y3)均在此函数图像上，且x1＜0＜x2＜x3，请比较y1、y2、y3的大小。

（4）若过A点作AP⊥x轴于点P，求三角形AOP的面积。

（5）如图4，若D、E、F是此反比例函数在第三象限图像上的三个点，过D、E、F分别作x轴的垂线，垂足分别为M，N、K，连接OD、OE、OF，设△ODM、△OEN、 △OFK 的面积分别为S1、S2、S3，则它们满足怎样的等量关系？

图4

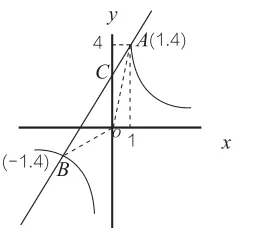
图5

（6）求经过点A、B的一次函数的解析式。

（7）如图5，连接OA、OB，设点C是直线AB与y轴的交点，求三角形AOB的面积。

（8）当x为何值时，反比例函数的值大于一次函数的值。

（9）在x轴上找一点P，使PA＋PC的值最小，求点P的坐标。

通过这一组问题链的设置，引导学生回顾已学的反比例函数的解析式求法、由图像观察反比例函数的增减性、与坐标轴形成的矩形或直角三角形面积与系数k之间的关系，然后继续探索反比例函数与一次函数结合后形成的函数值的大小比较问题以及面积问题等，在充分尊重学生思维发展的过程中，教师耐心地用“问题链”组织好教学，提“好问题”，提好“问题”，将反比例函数的知识点连成一串，涵盖一片，不仅开阔了学生的视野，更培养了学生综合解决问题的能力。

三、递进式设问，内化知识

课堂教学难度的设置，要尊重学生的认知规律，逐步递进进行，而不能是“一蹴而就”，如果没有把稳定而清晰的旧知识同化新知，那么模糊的认知将为后续新知的学习埋下障碍，教师必须认识到学生实现内化知识是需要过程的，一步一个脚印，从初步认识——理解掌握——灵活运用，所以递进式“变式”设问能很好地帮助学生激活数学学习的思维。

例如：在学习矩形的两个性质时：矩形的四个角都是直角；矩形的对角线相等。教师进行了以下变式设问：

（1）如图6，矩形ABCD的对角线AC、BD相交于点O，CO=5，求BD的长。

（2）变式1：如图7，矩形ABCD的对角线AC、BD相交于点O，CO=5，BC=8，则求△AOD的面积。

（3）变式2：如图8，矩形ABCD的对角线AC、BD相交于点O，CO=5，BC=8，求△ACD中AC边上的高。

（4）变式3：如图9，矩形ABCD的对角线AC、BD相交于点O，CO=5，BC=8，点M是BD上的一个动点，MF⊥AD，ME⊥AB，垂足分别为E、F，在矩形AEMF中连接EF，求EF的最小值。

（5）变式4：如图10，矩形ABCD的对角线AC、BD相交于点O，CO=5cm，BC=8cm，M是AD上 一 个 动 点，ME⊥AC，MF⊥BD，垂足分别为E，F，则ME+MF的值会随着点M的移动而改变吗？如果会变，请说明理由，如果不变，请求出ME+MF的值。

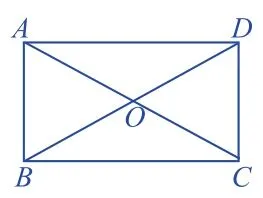
图6

图7

图8

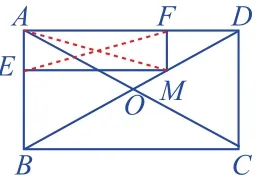
图9

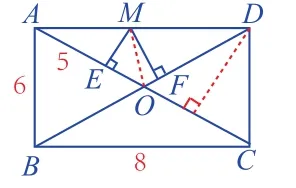
图10

通过这一组递进式变式的设问，让学生在巩固新学矩形性质的基础上层层推进，发现矩形的对角线将矩形分割成了四个等腰三角形和八个直角三角形，从而实现将矩形问题转化为所学的特殊三角形问题，让学生将新知与旧知完美转化，再进行了新的探究：矩形的对角线相等，所以可以进行互换转化，这样在及时巩固知识的过程中逐渐有序完善新知，最终帮助学生形成清晰的知识脉络，拾级而上的探究方式方能真正诱发学生的数学创造性。

建构主义认为认识不是主体对客观实在的简单、被动的反应，而是主体以自己已有的知识经验为依托所进行的积极主动的建构过程。所以知识的学习需要学生主体不断的探索。数学相对于其他学科来说，死记硬背的东西少，灵活应用的比较多，鉴于此，在课堂教学中更要注重学生主体探索和实践，在课堂上学生是主动的信息加工者，他们对信息进行主动的选择、加工和处理，不断地同化和顺应，从而构建新的认识结构。

那么在尝试解决问题的过程中，教师要帮助学生挖掘解决问题背后的思维过程，通过一系列不同形式、不同层次的问题设置引导学生从认识问题——探究问题——发现问题——实际应用，让有效的问题设置帮助学生学会揭示问题的深层结构，思考问题的规律性结论，发现解决问题的通性，从而在这个过程中领悟数学的思想和方法。