基于数学文化视角下的《勾股定理》

山东省东营市利津县第二实验学校 李积玲

近年来数学文化逐渐走进中小学课堂，深入实际数学教学，努力使学生在学习过程中真正受到文化的感染，产生共鸣，从而使学生体会数学的文化品位，体察社会文化和数学文化之间的互动越来越受到一线教师的重视。那么如何在初中数学课堂中进行数学文化的教学呢？下面以《勾股定理》教学案例和大家交流。

一、国外数学史上智慧的展现

课题：人教版数学八年级下册17.1勾股定理（第一课时）。

教学目标：（1）知识技能：理解和掌握勾股定理。（2）数学思考：经历探究勾股定理的猜想和证明过程，体会由特殊到一般的数学思想和多种方法解决问题的方法。（3）解决问题：应用勾股定理解决简单问题。（4）情感态度：学习古今中外数学家对数学的钻研精神和传承数学家的聪明才智。

教学重点：经历探究勾股定理的证明过程。

教学难点：多种方法证明勾股定理。

（一）情境再现

同学们，在我们学过的几何图形中，你觉得哪个图形最能代表数学？(三角形，如图1）其中直角三角形更是具有很多独特的性质，今天我们一起走进直角三角形。

你们知道吗，1970年我国发射第一颗人造卫星“东方红一号”飞入太空时，伟大的数学家华罗庚提出在卫星上携带几个直角三角形和几组特殊的数来向外星系展示地球的文明。他说：凡是有文明的地方，必然知道这些图形和数据的特定含义。你能猜出这其中的含义吗？难道直角三角形的三边长在数量上存在某些关系吗？

（二）发现与证明

那么直角三角形的三边长在数量上会有怎样的适量关系呢？

探究活动（发现篇）：传说2500多年以前，古希腊有一位数学家叫毕达哥拉斯，有一天在朋友家做客时看到朋友家的地板图案，沉思良久，惊喜地发现了直角三角形三边长的数量关系。那么我们一起看看到底是什么样的地板图案呢？你能说说这是什么样的地板图案吗？（由无数全等的等腰直角三角形组成的图案，如图2）你能从中发现直角三角形三边长的数量关系吗？（看不出来）毕达哥拉斯的眼中看到的是这样的图形。你现在有什么发现呢？（两个小正方形的面积和等于大正方形的面积，如图3）请说出你的理由？（一个小正方形是由两个等腰直角三角形组成的，一个大正方形是由四个等腰直角三角形组成的，所有直角三角形都全等，也就是面积是相等的，所以两个小正方形的面积和等于大正方形的面积）非常好，大家通过数一数、算一算的方法发现一种数量关系。那么对于这个等腰直角三角形三边长的数量关系又是怎样的呢？（a2+a2=c2或两直角边的平方和等于斜边的平方，如图4）

图1

图2

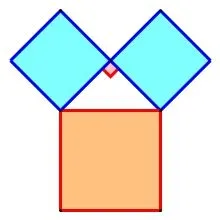
图3

图4

毕达哥拉斯虽然发现了等腰直角三角形的三边长之间存在数量关系，但是他更想进一步探究任意的直角三角形三边长的数量关系是否类似呢？于是他仍然借助网格再举两例，继续探究直角三角形的三边数量关系，下面是他的探究报告，请你帮他完成：

探究报告：

1.观察图案完成下列问题：图5中每个方格的边长都为1，图中A,B,C,A’,B’,C’为六个正方形。

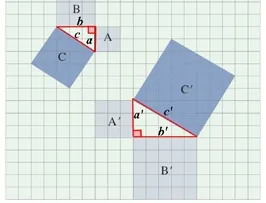
图5

②正方形C（如图6）的面积怎样计算呢？请说说，并画出、写出计算过程。（我是用补全的方法，如图7，把正方形C补成了一个更大的正方形，用最大的正方形的面积减去四个全等的小直角三角形的面积，得到了正方形C的面积）（我是用分割的方法，把正方形C分割成了四个小的全等的直角三角形和一个小正方形，如图8，用小正方形的面积加上四个全等的小直角三角形的面积，得到了正方形C的面积）（我算得正方形A的面积为4，B的面积为9，C的面积为13）

图6

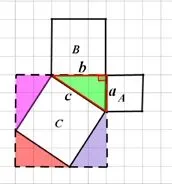
图7

图8

③通过计算，你发现三个正方形的面积之间有怎样的关系？（正方形A、B的面积之和等于正方形C的面积）

④由此你能猜想直角三角形的三边数量关系吗？（a2+b2=c2，如图9）

图9

图10

通过计算，你发现三个正方形的面积之间有怎样的关系？（通过图11，图12我算得正方形A’的面积为9，B’的面积为25，C’的面积为34））（正方形A’、B’的面积之和等于正方形C’的面积）

由此你能猜想直角三角形三边长的数量关系吗？(a2+b2=c2)

图 11

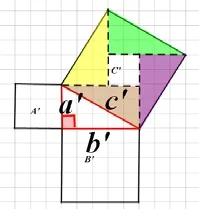
图 12

图13

2.综合以上列举的3个直角三角形的例子，你能猜想直角三角形三边长的数量关系吗？（如图13，直角三角形两直角边的平方和等于斜边的平方）

3.得到验证的这个猜想是否可以像定理一样直接应用来解决问题呢？（可以的）（不可以。以前学过猜想就是猜想，猜想是一个命题，命题要经过严格的推理证明，证明命题是正确的，才可以当作定理来应用的）那么如何证明我们的猜想“直角三角形两直角边的平方和等于斜边的平方”呢？

探究活动（证明篇）：证明命题：如图14，如果直角三角形的两直角边长分别为a,b，斜边长为c，那么a2+b2=c2。那么怎样才能证明这个命题呢？

图14

回归历史，毕达哥拉斯用他的地板图案发现并猜想出了直角三角形的三边关系，可惜没有借助地板图案证明这个猜想。在他之后的200多年，古希腊的另一位数学家欧几里得，给出了地板图案的完美证明，你能思考出欧几里得是怎样证明的吗？（如图15，是否可以将大正方形分成两部分？其中一部分的面积等于左边小正方形的面积；另一部分的面积等于右边小正方形的面积）真是一个大胆的猜想，你的想法和欧几里得的想法一样伟大。

图15

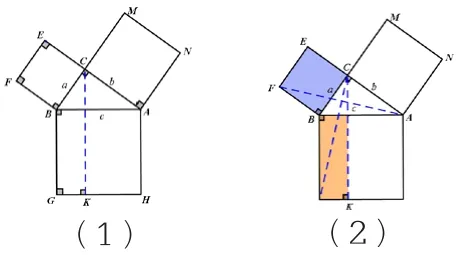
图16

那么如何证明一个正方形的面积会等于一个长方形的面积呢？如果直接几何证明是证不出正方形面积等于长方形面积的，能不能找另外的一个图形作为桥梁呢？（我觉得还是应该计算一下的，通过计算得到面积相等比较有说服力）(如果能用上我们学过的三角形知识就好了）如图16，我们构造两个三角形，这两个三角形会有怎样的关系呢？（全等）（理由是边角边）（奥，我发现这两个三角形的面积是相等的）那么每个三角形和小正方形、长方形在面积上又会有怎样的关系呢？（三角形和小正方形同底等高，面积是一半的关系）（三角形和小长方形同底等高，面积也是一半的关系）（我发现小正方形的面积和小长方形的面积是相等的）如图17。

图17

那么对于图18中右侧的正方形和长方形的面积是否也能证明相等呢？（同样的方法可以证明的）

图18

那么现在你觉得“命题：如果直角三角形的两直角边长分别为a,b，斜边长为c，那么a2+b2=c2”是正确的吗？（正确的）既然这个命题是正确的，那么我们就可以叫它定理了。得到“定理:如果直角三角形的两直角边长分别为a,b，斜边长为c，那么a2+b2=c2”。

（三）数学魅力的绽放

现在你能应用这个定理来解决华罗庚教授的数学问题吗?你认为几组直角三角形和几组数据之间有怎样的特定含义呢？能否举例和大家分享你的验证？（这几组数据反映的是这几个直角三角形的三边长度）（其中的特定含义就是直角三角形两直角边的平方和等于斜边的平方）（例如：3的平方得9,4的平方得16,5的平方得25，而且9加16正好等于25）

真不错，聪明的你揭示出了直角三角形的三边数量关系，你能应用这个关系解决下面的问题吗？

如图19所示，求出三角形的另一边长？

解：∵∠C=90°，

∴AC2+BC2=AB2，

即32+BC2=52，

BC2=25-9，

BC2=16，

∴BC=4。

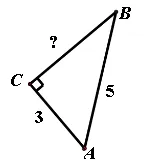
图19

所有的文化现象一样，数学文化直接支配着人们的行动，优秀的数学文化会是美丽动人的数学王后，得心应手的仆人，聪明伶俐的宠物伴随着先进的数学文化，数学教学会变得生气勃勃，灵动曼妙，光彩照人。

二、中国数学史上的美妙篇章

刚才我们一起回顾了古希腊的数学文化，从毕达哥拉斯到欧几里得，都用自己的方法发现并证明了直角三角形的三边关系，那么翻开我国的数学文化历史，中国的古人是如何发现并证明的呢？

在我国古代，人们将直角三角形中短的直角边叫勾，长的直角边叫股，斜边叫弦。根据我国古代数学书《周髀算经》记载，在距今3100多年前，人们就已经知道，如果勾是三、股是四，那么弦是五。后来人们进一步发现并证明了关于直角三角形三边之间的关系——两条直角边的平方和等于斜边的平方，并命名为勾股定理。

其中最为出名的是1700多年以前我国汉代的赵爽证明方法，你想试试吗？请大家两人为一小组，利用学具包中4个全等的直角三角形拼成一个正方形，并尝试证明勾股定理。如图20。

图20

这就是著名的赵爽外弦图、内弦图，他通过拼摆巧妙地利用面积关系证明了勾股定理，充分表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲，因此，这个图案被选为2002年在北京召开的国际数学家大会的会徽。

本节课主要学习了直角三角形的三边数量关系从毕达哥拉斯的发现中体会到从特殊到一般的研究数学问题的方法，无论国外、国内，上至帝王、总统，下至平民、学生，都用自己的方法证明着勾股定理，到目前已有500多种证法，他们为了研究数学，有时数十年为一日甚至一生地钻研一个问题，执着地追求真理，推动着数学的向前发展，这种精神值得我们学习，你试试，你也行的！

进入了21世纪，作为地球村的村民，我们一定要融入世界数学文化，将民族性和世界性有机地结合起来，数学文化离不开数学史，又不限于数学史，当数学文化的魅力真正渗入教材，到达课堂，融入教学时，数学就会更加平易近人，数学教学就会通过文化层面让学生进一步理解数学，喜欢数学，热爱数学。