解决立体几何问题中空间向量的运用

云南省曲靖市民族中学 李光所

一、立体几何问题中运用空间向量的价值

1．简化立体几何解题步骤

在立体几何问题解决中，运用空间向量思维方法可将空间问题转化为平面问题、几何问题转化为代数问题进行解决，简化立体几何的传统解题过程。空间向量主要解决的是点、线、夹角和距离之间的问题，这种解题方式可减少学生对数学思维的转换难度，同时将原题中的辅助线替代为坐标系，还能够促使解题步骤与过程的进一步简化，体现出空间向量解题的优越性。

在立体几何解题中，传统的解题方法是学生先利用相关的定理和公式明确解题思路，之后再运用多种思维进行转换，这样才能完成解题过程。传统解题方法过于复杂，对于思维转换能力偏差的学生而言，增加了解题的困难程度。而运用空间向量解决立体几何问题，虽然在一定程度上增加了计算过程的复杂性，但是却能够帮助学生快速理清解题思路，淡化由“形”到“形”的推理过程，进一步明确解题目的，提高学生解题能力。

3．赋予数学解题的简捷美

在立体几何解题中，可利用空间向量的直角坐标运算解决空间垂直与平行的问题，利用向量的夹角公式求出两条直线的夹角和线面夹角，利用向量的距离公式求出两点间的距离和两面角的平面角。通过运用空间向量方法解决较为复杂的立体几何问题，能够使解题过程清晰明了，解题书写内容简捷和谐。

二、在立体几何问题中空间向量的运用方法

空间向量主要运用于立体几何中的空间垂直证明、空间平行证明、空间角求解和空间距离求解四个方面，下面对垂直与平行问题和空间角问题的解题方法进行例题探讨。

1．空间向量在解决平行垂直问题中的应用

在运用空间向量证明线面平行时，应明确两种解题思路：一是可根据线面平行的判定定理，通过证明直线的方向向量与平面内一条直线的方向向量平行得出结论；二是通过证明直线的方向向量与平面的法向量垂直得出结论。在运用空间向量证明面面垂直时，也可采用两种解题思路：一是运用判定定理通过证明线线垂直得出结论；二是通过证明两个平面的法向量垂直得出结论。

例1 如图1 所示，在底面为矩形的四棱锥P-ABCD 中，ABCD，E 是PC 中点，F 是PD 中点，PA=AB=1，BC=2。求证：（1）EF ∥平面PAB；（2）平面平面PDC。

4.1.1 实施“亮证经营”制度，在超市显著位置设置食品安全信息公示栏，公示以下信息：食品经营许可证和营业执照；全部食品经营人员的健康检查证明（原件、复印件或者电子版）；门店负责人和食品安全管理员的照片、姓名、培训证明（原件、复印件或者电子版）。

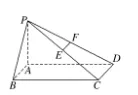
图1

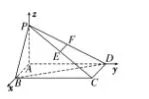
图2

证明：以A 为原点建立空间直角坐标系（如图2 所示），可知A（0，0，0），B（1，0，0），C（1，2，0），D（0，2，0），P（0，0，1），由此可获得

2．利用空间向量在空间角问题中的应用

在立体几何中，求空间角与距离是一类较为重要的问题，在历年的高考中均有此类题型出现，由此使得空间角成为立体几何教学的重点内容。在解决空间角问题的过程中，可对空间向量进行合理运用，通过空间向量的引入，能够为代数方法解决立体几何问题提供有效的工具。在解题时，可以用定量计算代替定性分析，这样一来，能够使烦琐的推理论证过程得以简化，有助于加快解题速度，提高解题效率。

例2 如图3 所示。在Rt △ABC 中，∠BCA=90°，现将△ABC 沿着平面ABC 的法向量平移至△A1B1C1的位置处，已知BC=CA=CC1，取A1B1、A1C1的中点D1和F1。求BD1与AF1所成角的余弦值。

解：以点C 作为坐标原点，建立空间直角坐标系C-xyz，具体如图4 所示。

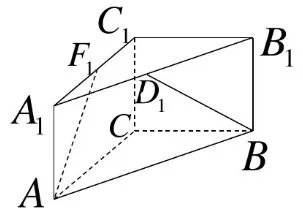
图3

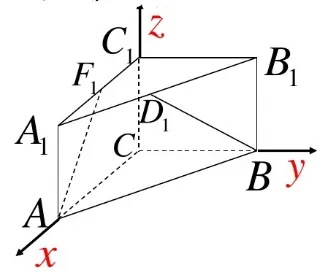
图4

设CC1=1，则

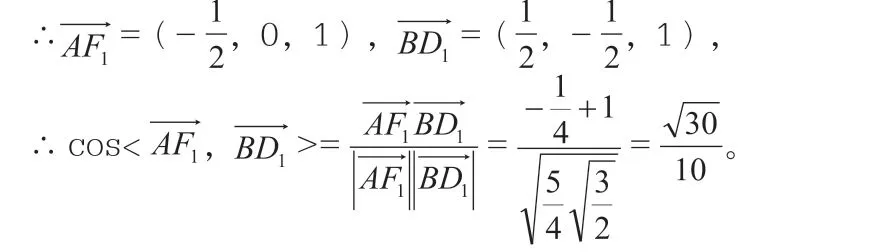
∴BD1与AF1所成角的余弦值为

例3 如图5 所示，在长方体ABCD- A1B1C1D1中，AB=5，AD=8，AA1=4，M 为BC1上的一点，且B1M=2，点N 在线段A1D 上，A1D ⊥AN。求AD 与平面ANM 所成角的正弦值。

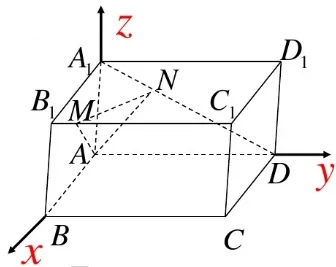
图5

解：由图可知，A（0，0，0），A1（0，0，4），D（0，8，0），

通过上述例题的分析可以看出，在空间角求解中，对空间向量进行运用，能够使烦琐的解题过程得以简化，为学生快速求解提供了有效的方法。

总而言之，在高中数学教学中，将空间向量运用到立体几何问题的解决中来，有利于简化解题过程，帮助学生形成完整的解题思路，对培养学生发散性思维和提升学生数学学习能力起着积极作用。在数学解题中，教师要引导学生掌握空间向量解决立体几何平行问题、垂直问题、空间距离问题以及空间角问题的方法，帮助学生提高解题效率和准确性。