2018年中考数学文化型试题背景赏析

余小芬 闵蓉 刘成龙

[摘  要] 文章分析了2018年中考数学文化型试题的六类命题背景：以“算经十书”为背景，以《数书九章》为背景，以《算法统宗》为背景，以“勾股定理”证明为背景，以“割圆术”为背景，以“杨辉三角”为背景.

[关键词] 中考数学;试题背景;数学文化;赏析

数学是人类文化的重要组成部分，数学课程应适当反映数学的历史、应用和发展趋势……数学科学的思想体系、数学的美育价值、数学家的创新精神、数学课程应帮助学生了解数学在人类文明发展中的作用，逐步形成正确的数学观. 所谓数学文化，从狭义上讲是指数学的思想、精神、方法、观点、语言，以及它们的形成和发展;从广义上讲就是除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等. 2011年版《义务教育数学课程标准》指出：“数学文化作为教材的组成部分，应渗透在整套教材中.为此，教材可适时地介绍有关背景知识，包括数学在自然与社会中的应用，以及数学发展史的有关材料，帮助学生了解在人类文明发展中数学的作用，激发学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美. ”因此，在各版本的初中数学教材中，涌现了一大批与数学文化有关的阅读材料或例题、习题，例如“方程”史话、杨辉三角、漫画勾股世界、海伦——秦九韶公式、投针实验等等. 这些内容的设置，不仅有利于弘扬博大精深的数学文化，还能激发学生的数学学习兴趣，开拓学生视野，帮助学生理解数学、热爱数学，从而不断提升他们的数学核心素养. 近年来，以数学文化作为试题背景已成为中考命题的新亮点、新趋势. 例如2015年湖南常德中考以“角谷猜想”为背景考查代数式的运算，2016年孝感中考以“赵爽弦图” 为背景考查正方形性质、正切三角函数定义，2016年盐城中考以“费马点”为背景考查线段长度最值问题等. 2018年，各地中考坚持“立德树人”“文化育人”的基本理念，命制了一批背景丰富的数学文化试题，本文对这些优秀试题的命题背景进行赏析，以飨读者.

以“算经十书”为背景

“算经十书”是中国传统数学的经典. 所谓“算经十书”，指的是中国十部古算书：《周髀算经》《九章算术》《孙子算经》《五曹算经》《夏侯阳算经》《张丘建算经》《海岛算经》《五经算术》《缉古算经》《缀术》（元丰年间已失传，后来以《数术记遗》代之）. 唐代国子监内设算学馆，置有博士、助教，指导学生学习数学，规定这十部书作为课本. “算经十书”分别总结了当时的数学成就，对数学的发展起到了巨大的推动作用，构成了具有中华民族自身特色的传统数学体系.

例1  （2018年江西中考第9题）中国的《九章算术》是世界现代数学的两大源泉之一，其中有一问题：“今有牛五、羊二，直金十两. 牛二、羊五，直金八两. 问牛羊各直金几何？”译文：今有牛5头，羊2头，共值金10两;牛2头，羊5头，共值金8两. 问牛、羊每头各值金多少？设牛、羊每头各值金x两、y两，依题意，可列出方程组为__________.

评析  《九章算术》是中国古代第一部数学专著，是“算经十书”中最重要的一种. 该书内容十分丰富，全书采用问题集的形式，收集246个与生产、生活实践有联系的应用问题，系统总结了战国、秦、汉时期的数学成就. 同时，《九章算术》在数学上还有其独到的成就，不仅最早提到分数问题，也首先记录了盈不足等问题. “方程”这章还在世界数学史上首次闡述了负数及其加减运算法则. 《九章算术》是一本综合性的历史著作，是当时世界上最先进的应用数学，它的出现标志中国古代数学形成了完整的体系. “方程”是《九章算术》的第八章，“方程”指的是一次方程组，而一次方程组又是利用算筹（算筹表示未知数的系数及相应的常数项）布置而成的，其形状有如方阵，故称之为方程. 我国古代数学家刘徽在《九章算术注》指出：“程，课程也. 二物者二程，三物者三程，皆如物数程之，并列为行，故谓之方程.” 本题根据“牛的单价×牛的数量+羊的单价×羊的数量=总价”，不难得到方程组为5x+2y=10，

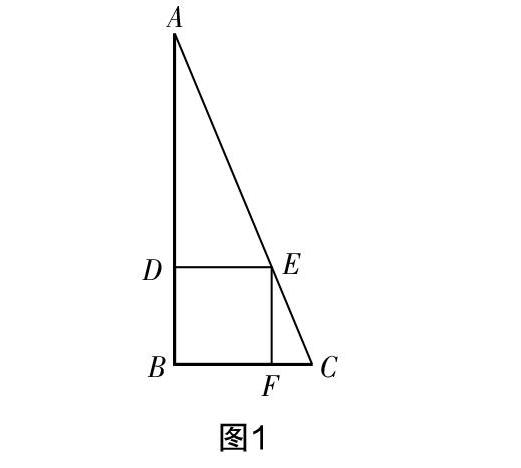
例2  （2018年岳阳中考第15题）《九章算术》是我国古代数学名著，书中有下列问题：“今有勾5步，股12步，问勾中容方几何？”其意思为：“今有直角三角形，勾（短直角边）长为5步，股（长直角边）长为12步，问该直角三角形能容纳的正方形的边长最大是多少步？”

评析  “勾股”是《九章算术》的第九章，主要介绍利用勾股定理求解各种问题. 本题以《九章算术》中几何问题为背景，考查对勾股定理的应用及求解直角三角形的最大内接正方形. 如图1，设在Rt△ABC中，能容纳的最大正方形DEFB的边长为x，由相似不难得到=，即=，解得正方形边长x=.

特别指出，2018年全国各地中考中，以《九章算术》为背景考查列（或解）一次方程组的试题较多，比如2018年湖北襄阳中考第13题、2018年河南中考第6题、2018年广州中考第8题、2018年湖北宜昌中考第19题等.

例3  （2018年安徽中考第16题）《孙子算经》中有这样一道题，原文如下：今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽. 问：城中家几何？大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完. 问：城中有多少户人家？请解答上述问题.

评析  《孙子算经》作者及成书年代不详，传本的《孙子算经》共三卷，上卷、中卷系统叙述了算筹记数法和筹算的乘、除、开方及分数等计算的步骤及法则，以及简单的面积、体积的计算问题. 下卷是各种应用问题，其中著名的“物不知其数”：“今有物不知其数，三三数之余二，五五数之余三，七七数之余二，问物几何？”举世闻名，被誉为“中国剩余定理”或“孙子定理”. 还比如经典问题“鸡兔同笼”： “今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”更是古今中外“鸡兔同笼”问题的始祖.

本题以《孙子算经》中分鹿问题为背景，考查学生对一元一次方程的理解. 由题意，可设城中有x户人家，于是有x+=100，从而解得城中有75户人家.

以《数书九章》为背景

《数书九章》又被称作《数学大略》《数学九章》，其作者是我国南宋著名的数学家秦九韶（1202—1261年）. 《数书九章》全书九章十八卷，九章九类：大衍类、天时类、田域类、测望类、赋役类、钱谷类、营建类、军族类、市物类，每类9题，共81题. 该书内容丰富至极，上至天文、星象、历律、下至河道、水利、建筑、运输，包括各种几何图形和体积，钱谷、赋役、市场、牙厘的计算和互易. 《数书九章》在一次同余式组解法和高次方程数值解法等方面取得了具有世界意义的光辉成就，我国数学史家梁宗巨对其这样评价：“《数学九章》是一部划时代的巨著，内容丰富，精湛绝伦. ”秦九韶也被美国著名科学史家萨顿誉为是“他那个名族，他那个时代，并且确实也是各个时代最伟大的数学家之一”.

例4  （2018年长沙中考第11题）我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题目中的“里”是我国市制长度单位，1里=500 m，则该沙田的面积为（    ）

A. 7.5 km2         B. 15 km2

C. 75 km2          D. 750 km2

评析  本题以《数书九章》中问题为背景，考查对勾股定理的应用. 根据题目中数据，不难得到52+122=132，故这个三角形是直角三角形. 再根据单位换算得：5里=2.5 km，12里=6 km，故该沙田的面积为×2.5×6=7.5 km2.

以《算法统宗》为背景

《算法统宗》是明代数学家程大位所著，它是一部以珠算为主要计算工具的应用数学著作. 全书共收集了595个问题，并穿插有大量的图形和诗词形式的歌诀. 梁宗巨先生指出：“明代在西方数学输入之前，最大的成就可以说是珠算的发明，最重要的数学书要算程大位的《算法统宗》. ”

例5  （2018年邵阳中考第10题）程大位是我国明朝商人，珠算发明家. 他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法. 书中有如下问题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁. ”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，问大、小和尚各有多少人？下列求解结果正确的是（    ）

A. 大和尚25人，小和尚75人

B. 大和尚75人，小和尚25人

C. 大和尚50人，小和尚50人

D. 大、小和尚各100人

评析  本题以经典问题“百僧分百馒”为背景，考查二元一次方程组及其解法. 由题意，设大和尚有x人，小和尚y人，不难得x+y=100，

3x+=100， 故解得大和尚25人，小和尚75人.

2018年取材于《算法统宗》的中考试题还有福建中考第8题、浙江绍兴中考第12题等.

以“勾股定理”证明为背景

例6  （2018年成都中考第22题）汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝. 如图2所示的弦图中四个直角三角形都是全等的，它们的两直角边之比均为2 ∶ 3. 现随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为_________.

评析  《周髀算经》是流传到现在的一部最早的数学著作，同时也是一部“盖天说”（中国古代的一种宇宙观，认为天像一个斗笠，大地像一个翻扣的盆）的天文学著作. 《周髀算经》约成书于公元前100年，全书共二卷，内容是一些天文历法及有关的数学问题，所包含的数学内容有分数计算、等差数列、勾股定理和测量等. 特别是关于勾股定理的论述，比毕达哥拉斯要早六百多年. 从古至今，《周髀算经》可以说是最纯粹的中国国粹之一. 据史书记载，《周髀算经》并未直接给出勾股定理的证明方法，而是汉代数学家赵爽利用弦图对此进行了证明. 弦图精妙地展现了几何图形的截、割、拼、补，其构思精巧，富有创意，既表达着逻辑的严谨，又呈现了几何的直观，是数形结合的典范. 本题以赵爽弦图为载体，考查勾股定理和几何概型.

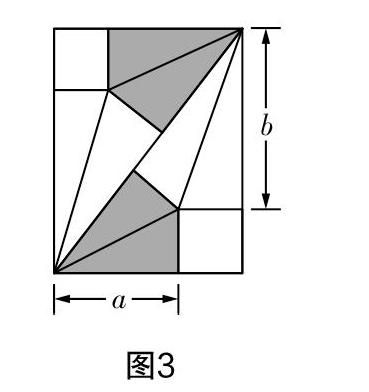
例7  （2018年温州中考第10题）我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两个全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得到的图形证明勾股定理. 如图3所示的矩形由两个这样的图形拼成，若a=3，b=4，则该矩形的面积为（    ）

A. 20     B. 24C. D.

评析  本题以数学家刘徽对勾股定理的证明为背景，让学生从另一角度欣赏了图形的割补技巧，感受我國数学文化的博大精深，感悟古代数学家的智慧和才能. 问题解决的关键是计算出小正方形的边长，图5的矩形由两个直角三角形构成，每个直角三角形的边长均满足勾股定理：（x+3）2+（x+4）2=（3+4）2，其中x为小正方形的边长，由此解出x，得到矩形的面积为（x+3）（x+4）.

以“割圆术”为背景

魏晋时期的数学家刘徽首创割圆术，为计算圆周率建立了严密的理论和完善的算法. “割圆术”是以圆内接正多边形的面积来无限逼近圆面积，即“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣. ”“割圆术”通过无限分割的方式，体现了有限到无限、以直代曲的极限思想.

例8  （2018年宜宾中考第13题）刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积. 设☉O的半径为1，若用外切正六边形来近似估计☉O的面积，则S=______（结果保留根号）.

评析刘徽用割圆术证明“半周半径相乘得积步”的圆面积公式时，正是从内接正六边形（“六觚”）开始割圆，依次得到内接正十二边形（“十二觚”）、正二十四边形（“二十四觚”）……认为割圆到最后就得到一个和圆重合的正无穷多边形. 本题就以“割圆术”的最简单情形（正六边形）为背景，考查多边形的内角和、锐角三角函数、勾股定理、三角形面积等基础知识. 如图4，由ABCDEF为正六边形得△ABO为等边三角形，又☉O的半径为1，故OG=1，BG=AG=，因此AB=，所以S=6S=6×××1=2.

以“杨辉三角”为背景

“杨辉三角”是我国宋朝数学家杨辉于1261年在其所著《详解九章算法》一书中提出的，欧洲人将杨辉三角称为“帕斯卡三角”（于1654年由法国人帕斯卡发现）. 由此可见，我国比欧洲至少要早三百年发现这一伟大成果. “杨辉三角”结构对称优美，蕴含丰富的规律和结论，古往今来、古今中外，吸引着无数数学爱好者去认识它、研究它. 同时，它也是现行高中教材中二项式定理中的重要内容，是中考、高考命题的良好素材.

例9  （2018年宜昌中考第8题）1261年，我国南宋数学家杨辉用图5中的三角形解释二项和的乘方规律，比欧洲的相同发现要早三百多年，我们把这个三角形称为“杨辉三角形”. 请观察图中的数字排列规律，则a，b，c的值分别为（    ）

评析  本题以“杨辉三角”为背景，考查学生的观察能力，不难发现“杨辉三角形”左右两边上的数都是1，其余的数为它肩上的两数之和，故a=1+5=6，b=5+10=15，c=10+10=20.

总之，中考试题中渗透数学文化，不仅弘扬了古今中外数学所取得的卓越成就，推广了数学经典著作，而且帮助学生开阔了眼界、增长了知识、启迪了心智.

基金项目：四川省“西部卓越中学数学教师协同培养计划”项目（ZY16001）.

作者简介：余小芬（1986-），四川内江人，硕士，讲师，主要研究方向：数学教育及中高考研究;闵蓉（1999-），四川眉山人，內江师范学院数信学院数学与应用数学专业2017级3班学生;刘成龙（1985-），四川内江人，硕士，讲师，主要研究方向：数学教育及中高考研究.