数学思想方法在初中科学教学中的渗透探讨
摘 要:随着教学改革的深入落实,初中教育的教学方法、教学理念都在不断地创新和优化。在初中数学教育当中,数学思想方法的应用价值较高,其不仅可以有效培养学生的学习思维,同时对于促进学生的学习效率、质量的提高也有显著性的提升作用。对此,为了更好地提升初中科学教学水平,文章详细分析了数学思想方法在初中科学教学中的渗透。
关键词:数学思想方法;初中科学;教学渗透
一、化归思想
化学思想主要是将未解决或有待解决的问题借助转化的方式进行分析,将生疏转化为熟悉,将抽象转化为具体。将这一些问题归结到已经解决或容易解决的问题当中,促使问题最终得到解决。例如,在反弹击物的案例当中,问题主要是在平面镜前发射小球并借助反弹然后击中物体时,选择发射的最佳方向[1]。对于这一问题,虽然情境比较陌生,但是因为学习过平面镜的反射原理,所以可以将反弹击物的问题转化为平面镜反射的问题,这样的方式可以更好地理解问题,从而实现对问题的解决。在实际教学中,如果问题比较复杂,無法借助一次性化归解决,此时便可以采取连续性的化归,直到化归为一个容易解决或已经解决的问题中。
二、数形结合思想
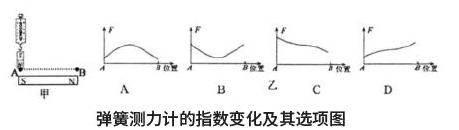
在初中科学教育当中将代数的问题以图形方式进行表示或者是将几何问题以代数的方式进行表示都是数形结合思想的有效体现,这一思想能够将一些烦琐、复杂的知识点转变为更加容易解决的形式,从而实现问题的有效解决[2]。例如,题目“如下图,在水平地面上的磁体上,有一个挂有弹簧测力计的小磁体。现在提着弹簧测力计顺着水平磁体缓慢移动,弹簧测力计的指数会随着位置的变化呈现怎样的变化”。对于这一问题,首先需要明确小磁体与大刺激之间的吸引力,之后随着磁体的移动分析作用力是否发生改变。其次,采取对整个过程的归纳,发现磁体吸引力会逐渐减少并为零,然后受到逐渐增大的排斥力。最后,在选项当中的曲线变化吸引力会逐渐减少,此时拉力也会逐渐减少。伴随着排斥力的提升拉力会逐渐减少,此时拉力会一种减少,所以C为最佳答案。在这一题当中,数形结合的思想主要是让学生从不同角度对题目进行理解,强化对问题的理解,并提供问题的有效解决途径,对于学生实际问题转变为数学问题的能力有一定的培养。数形结合的途径在于数轴,借助数轴内容展现出数和点的对应关系,此时学生学习效果得到了提高。应用数形结合的方式让学生将抽象的数量关系以形象的几何直观性表现出来,同时也能够将几何图形的问题转化为数量关系的问题进行解决。
三、集合思想
集合思想的应用主要是体现在关系的不同概念内容之间。应用集合思想方法的区分方式可以提高学生对于概念以及物质特点的记忆效果,同时可以借助集合思想实现对部分问题的解决,解题过程会更加简洁、高效率。应用集合思想的解题步骤主要是以构建集合、应用子集、交集、并集、补集等途径解题的。
综上所述,在初中科学教育当中,数学思想方法的应用途径还有很多,例如观察与实验、分析与综合、归纳与演绎等。在课堂教学中,教师需要遵从初中科学教学内容的要求,在教学中根据教学目标、教学内容以及教学习惯等因素针对性采取可以提高教学质量的数学思想方法,挖掘教材当中有价值的数学思想,从而有意识、有目的性以及有计划性地进行渗透,减少和规避盲目性与随意性。另外,在初中科学教育中渗透数学思想方法不仅有利于初中科学教学水平的提升,对于学生的数学学习能力、知识掌握能力等均有一定提升作用,教师应当在教学中坚持这一教学方法。
参考文献:
[1]孙成林,李焱.中考试题的命制对初中化学学科思想方法教学的启示[J].化学教学,2017(4).
[2]朱少祥.基于“奇趣”思想的初中化学教学策略——以人教版“水的组成”课题为例[J].化学教学,2016(11):233-234.
作者简介:林祖远(1984—),男,浙江苍南人,中学一级教师,本科,研究方向:初中科学教育。

