中日初中学段数学课程标准“数与代数”比较研究

黄思婷，朱 哲

（浙江师范大学教师教育学院，浙江 金华 321004）

“数与代数”是义务教育阶段数学四大课程内容之一，是研究现实世界事物的数量关系及其变化规律的数学模型，可帮助人们从数量关系的角度更准确地认识、描述和把握现实世界。[1]TIMSS2015评价框架，八年级评价的内容领域中“数与代数”共占60%，其中“数字”占30%，“代数”占30%，可见“数与代数”的重要性。中国和日本都属于数学教育优质的亚洲国家，故中国和日本的数学课程标准具有可比性。通过对中国现行、日本即将实行的课标中“数与代数”内容的比较，努力从中获得些许启示，为数学课程改革提供思考。

一、研究内容与方法

对中日数学课标中“数与代数”领域的内容标准进行比较分析，其中日本为《初中数学学习要领》（下文简称《要领》），于2017年3月颁布，2021年4月起施行。中国为《义务教育数学课程标准（2011年版）》（下文简称《标准》），由中华人民共和国教育部于2011年12月颁布，2012年秋季开始实施。

对两国数学课标“数与代数”内容进行比较分析，主要回答几个问题：课标中“数与代数”内容广度如何？内容有何特征？内容的学习要求深度如何？学习要求有何特征？

TIMSS2015数学框架由内容维度和认知维度组成，课程内容与认知要求共同构成了课程标准中的内容标准，基于数学框架等理论分析，将从主题维度、认知维度两方面进行剖析，且采用量化比较和质性分析相结合的方法。

二、研究结果

用量化比较和质性分析相结合的方法对主题、认知两维度进行分析，得到如下研究结果。

（一）主题维度

初中学段，《课标》将“数与代数”领域分成三个维度：数与式，方程与不等式，函数；《要领》的相关内容分为“数与式”“函数”两个知识模块，涉及四个维度，即数与运算、代数式、方程、函数。综合两者的维度，将“数与代数”领域分成五个主题维度：数与运算、代数式、方程、不等式、函数。

1.主题维度的量化比较

统计五个主题维度下的内容条目，其中内容条目以最小的任务要求为基本单位，并用内容条目数刻画内容广度，具体如表1。

从表1可得，《课标》的内容条目总数要多于《要领》的内容条目数，在“数与代数”领域中《课标》的广度要大于《要领》。“方程”维度中两者的内容条目数相同，即广度相同；其余四个维度，《课标》的内容条目数均大于《要领》，即广度大于《要领》。《要领》中“代数式”“方程”的占比要高于《课标》，其余三个维度均低于《课标》，其中《要领》中“代数式”和“函数”的占比相同，且占比最高；《课标》中“函数”占比最高，其次为“数与运算”“代数式”；“不等式”内容的占比均为最低。

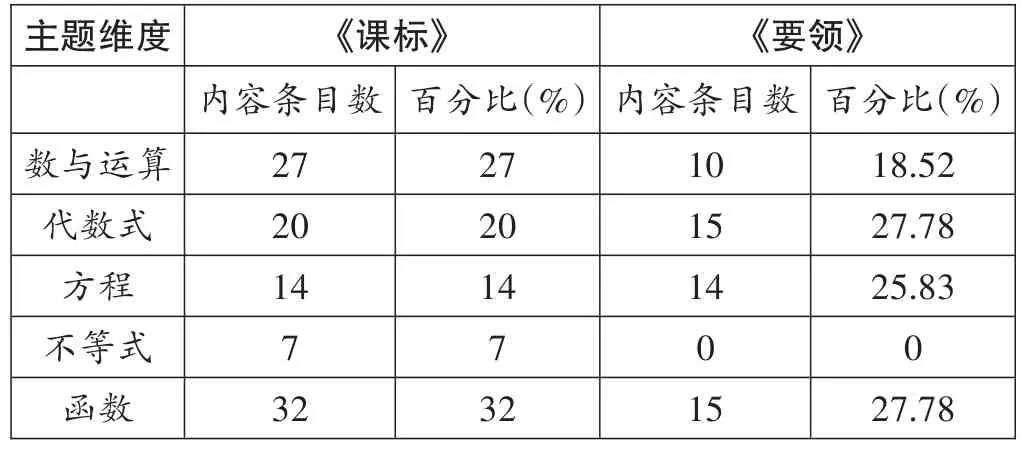
表1 “数与代数”主题维度的内容条目数及其百分比表

2.主题维度的质性分析

《课标》和《要领》的五个主题维度内容相似，但存在差异，从主题覆盖程度、主题逻辑结构两方面对每个维度进行分析。

（1）数与运算

在主题覆盖程度上，均出现“有理数、四则运算及应用”“平方根及运算”“无理数”的内容。《要领》学习有理数、无理数、四则运算和简单应用，没有明确将数的范围扩充到实数；用a×10n的形式表达处理误差与近似值，该表示可明确数字的准确性、估计错误的范围，具有针对性和精确性。《课标》借助负数将数系扩充到有理数，再由根式运算认识无理数，完成到实数的扩充，并将实数与数轴上的点一一对应；借助数轴理解相反数和绝对值，渗透数形结合思想；用有理数估计无理数的大致范围，借助旧知理解新知，学生提升估算能力且培养数感。

在主题逻辑结构上，《要领》：正数与负数；四则运算；应用→平方根；运算；灵活运用→有理数、无理数。《课标》：有理数；运算；应用；绝对值、相反数→平方根、立方根；运算→无理数；实数→近似数。两者的逻辑结构基本一致——扩充数系，通过运算及应用等，培养数感与运算能力，并关注数感培养的阶段性与发展性。《课标》初中完成实数的数系扩充，相比较完善逻辑结构的进程比《要领》快。

（2）代数式

在主题覆盖程度上，均出现“代数式、运算及应用”“单项式、多项式及四则运算”“因式分解”的内容。日本在小学已掌握用字母表示数，具有符号意识，初中重点是用字母表示数量关系和定理等，提升运算与数学表达的能力；《要领》讲解代数式的除法，不涉及除式间的运算；因式分解是乘法公式展开的逆运算，重视十字交叉的掌握及应用。《课标》认识字母表示数具有一般意义，建立符号意识；类比数的运算，认识到代数式的形式变换，本质是恒等变换，并非单纯的字母游戏，对提高运算能力，培养数感与符号意识、类比思想均具有重要意义。

在主题逻辑结构上，《要领》：单字母代数式的四则运算；代数式的建立→单项式、多项式各自的四则运算；代数式的应用→单项式与多项式的乘法、除法运算→乘法公式；因式分解。《课标》：用字母表示数；代数式表示及求值→整式的加法、减法、乘法→乘法公式；因式分解→分式；分式的四则运算。《要领》中代数式四则运算的分类依据代数式的类型，考虑到知识的阶梯性与学生的阶段性，重视知识的螺旋式上升。《课标》先学习整式加法、减法、乘法的内容，包括乘法公式与因式分解，最后引进整式的除法与分式运算。相比较，《课标》注重逻辑结构的完整性，《要领》更重视学生的阶段性、知识的逻辑性。

（3）方程

在主题覆盖程度上，均出现“（解）一元一次方程及应用”“（解）二元一次方程”“（解）一元二次方程”的内容。《要领》重视方程的应用；《课标》结合实际问题检验方程根的合理性。方程是刻画数量间等量关系的数学模型，由具体问题的数量关系列出方程，培养学生数学建模的核心素养。

在主题逻辑结构上，两者均遵循一元一次方程→二元一次方程组→一元二次方程的逻辑，两者的逻辑结构基本一致。

（4）不等式

《要领》没有解不等式的相关内容，但介绍数量间有等式或不等式两种关系。《课标》结合具体问题，解一元一次不等式（组）并用数轴表示解集，强调不等式与方程之间的联系，从等量关系到不等关系，学生掌握迁移、转换与类比的数学思想方法。

（5）函数

在主题覆盖程度上，均出现“函数”“一次函数表达式、图像、变化情况与应用”“二次函数表达式、图像、性质、变化情况与应用”的内容。《要领》在学习比例关系基础上借助函数的观点理解量的变化关系，重视具体问题的变域（定义域和值域）；从二元一次方程的观点观察一次函数，得到二元一次方程的解是平面直角坐标系中两条直线的交点，这些交点组成的图形为该一次函数图像；一次函数y=ax+b，a为斜率决定直线的倾斜角度与增减；只学习特别的二次函数y=ax2，不涉及一般的二次函数。《课标》讲解一次函数y=kx+b（k≠0），k 的正负和图像增减的关系，未明确决定直线的倾斜程度；学习反比例函数的图像及变化情况；用描点法画二次函数的图像；二次函数一般式与标准形的转换，得到顶点坐标、开口方向与对称轴等；利用二次函数图像得一元二次方程的近似解，体现数形结合的数学思想方法，同时借助函数深化对方程的理解。

在主题逻辑结构上，《要领》在学习比例式与反比例式的基础上，引入一次函数和二次函数，《课标》指导下“函数”的学习顺序基本有两种，具体如表2。相比较，《课标》中“函数”逻辑结构的完整性比《要领》高，《要领》学习函数的顺序更符合学生的认知规律。

表2 函数学习的顺序表

（二）认知维度

在分析“数与代数”主题维度的基础上，对内容的学习要求进行分析，得到认知维度的相关结论。

1.认知维度的量化比较

美国心理学家布卢姆提出教育目标分类学理论，将教育目标分为认知领域、情感领域和动作技能领域三个主要部分。TIMSS2015评价框架中的“认知领域”分为了解、应用和推理三类。参考并结合认知维度相关框架，得到表3，将“数与代数”领域的认知维度分为四个递进的要求层次：A，B，C，D，分别赋值1，2，3，4，对总要求进行求和，再得到算数平均值，以该值作为认知深度。[2]

表3 学习要求赋值表

通过对“数与代数”内容的学习要求进行分类、统计、求和、算平均，得到课标的认知深度，具体如表4。从表可得，两者在“数与代数”领域的认知深度基本一致，但《课标》的学习要求数远多于《要领》，这与上述《课标》内容广度比《要领》大保持同步，同时体现《课标》中“数与代数”内容广而不深的特点。

在学习要求层次分布上，《课标》层次B的占比（48.91%）比《要领》低（77.05%），其他三个层次的占比均比《要领》高，其中层次A（26.09%）、层次C（15.22%）的占比远高于《要领》（9.84%，4.92%），层次D两者的占比基本相同。《课标》和《要领》的层次B占比均最高，《课标》层次D的占比最低，《要领》层次C的占比最低，则高水平层次的要求占比低于低水平层次的要求，强调掌握并应用具体内容解决简单实际问题，但并不多，主要还是以基础知识的了解、理解等为主。

2.认知维度的质性分析

在量化比较的基础上，从内容要求的语言表述、学习内容的处理、与信息技术结合三方面对学习要求进行质性分析。

在内容要求的语言表述上：《标准》对每个知识内容都提出准确且具体的要求，并用丰富的动词进行描述，如“能用/解/比较”“会用/求”等，并在内容要求的基础上配套相关的实例加以理解。《要领》的行为动词也非常丰富，且具有一定的层次性，但对各个知识点的要求的具体性与准确性不足，比较宽泛，如“在具体场景中使用”“考虑并表达”等；没有配套相关的实例，但每一年级的模块内容后均给出“数学活用”和“内容处理”。其中“数学活用”内容基本相同，强调通过数学活动培养学生发现、分析和解决问题并进行表述的能力，旨在掌握知识与技能的基础上培养学生数学思考力、判断力和表现力；“内容处理”联系四个模块的内容，也考虑到自小学至高中阶段相关内容的衔接，具有很强的指导意义。[3]

在学习内容的处理上：《课标》重视与现实生活的联系，如“借助现实情境”“分析具体问题”“根据特定问题”等，结合生活情境或具体实例，培养运用数学解决实际问题的能力，提升学习数学的兴趣等；现实中的问题一般有多种解决方案，同一问题启发学生从不同角度入手，比较不同的方法，加深对所建模型的理解，并尝试寻找最优化的数学模型，培养数学建模的核心素养。《要领》重视对所掌握的知识进行数学表达的能力，强调与具体场景结合相关知识方法的表述，如“表达与具体场景相关的线性加减法的方法”“表达基于方程性质求解线性方程的方法”等，注重培养学生的思考力、判断力与表现力。

在与信息技术结合上：《课标》多个知识点借助信息技术简化运算、理解知识等，如“会用计算器求平方根和立方根”“能用计算器进行近似计算”“能根据特定问题查阅资料”等。《要领》在内容方面并没有体现与信息技术的结合，但在“指导计划的写作与内容处理”中考虑可适当地使用计算器等信息技术手段提高学习效率。

表4 “数与代数”各层次学习要求数目统计表

三、结论与思考

1.比较的结论

（1）在主题维度上，《课标》的内容广度要大于《要领》。两国课标的基本内容类似，但存在差别：《课标》更重视知识逻辑结构的完整性，且相关内容的学习进程一般比《要领》快；《要领》知识编排考虑学生的阶段性与发展性，重视学生的认知规律。

（2）在认知维度上，两者课程深度基本一致，但《课标》的学习要求远多于《要领》，这体现《课标》内容广而不深的特点。两者均重视基础知识与基本技能，低水平要求高于高水平要求；《课标》重视学生在现实情境中理解、应用知识；《要领》重视学生的数学表达能力，在具体场景中表述所学知识；《课标》在信息技术结合方面的体现度比《要领》高。

2.对数学课程改革的思考

（1）发扬“双基”优势，提升学生表现力与应用意识。《要领》的特点之一是“资质与能力的培养”，其中包括“知识与技能”“思考力、表现力与判断力”“学习志向、能力与人性”三个支柱。“知识与技能”即掌握基础知识与基本技能，并做到自主地掌握。“思考力、表现力与判断力”指从这三个视点出发，谋求知识技能与实际生活的联系，并将知识技能与三力相互关联、融合和深化。“学习志向、能力与人性”包括不断创新知识技能的学习意欲和态度，尊重他者和不同社会的价值观并与之共处，重视自然和环境并与之共生，培养自主学习能力、独立思考能力等。结合我国的国情，发扬注重“双基”的优势，培养学生的核心素养，借鉴国外“发展思考力、表现力和判断力”“注重培养学生的应用意识”等理念与经验[4]，鼓励学生在具体情境中将习得的知识与技能进行表达与应用，实现中国特色的数学课程体系的进一步完善。

（2）课程的内容的选取和编排要考虑学生的阶段性，加强知识间的衔接性。充分考虑学生的阶段性和知识间的衔接性，在学生最近发展区内设置内容，提升学生学习数学的自信。基于此教师引导学生主动、自动地学习数学，培养其学习动机，并在取得一定学业成就的同时予以及时的鼓励。《要领》分年级给出内容标准，考虑知识的层次性与学生的阶段性，且幼儿园到高中的要领基本是同时修订且实行的，知识间的衔接性较强。《课标》偏重知识逻辑结构间的完整性，课程内容有“广而不深”的特点，可在学生学力能及的情况下，适当拓宽当下知识点的深度，并运用螺旋式的编排方式，基于新知加深对旧知的理解，实现知识“既广又深”。同时充分结合数学知识的内在逻辑、学生螺旋的心理逻辑等，编写恰当的数学教材。

（3）加强“数与代数”教学与信息技术的有机整合。《课标》中多个内容条目借助信息技术，“数与代数”领域的知识与信息技术的结合是必然的。[5]这种必然性需在数学教学中加以体现，一方面信息技术的使用可简化繁琐的计算，同时让学生有时间去关注问题的本质而不仅停留在计算层面；另一方面，信息技术的使用能显示概念的本质属性与特征，能使得一些知识形象化，如函数和图像的结合，学生可直观感知函数的变化情况等，更易理解和掌握知识，从而提高教学的效果。在信息技术的支持下，学生能通过查找文献了解知识的背景；与教师进行观察、探究、推理与交流等数学活动，能积累数学活动经验，培养探究精神，有利于创造性地解决问题。▲