追根溯源探本质 求简重悟促发展——《植树问题》的教学思考与实践

□ 李 静

一直以来，植树问题都是人教版“数学广角”各类研究课、公开课的经典选择。课堂上，教师能顺利引导学生得出三种模型的公式，学生也能说得清楚明白。然而一旦运用到解决实际问题中，很多学生就判断不出到底是该“加1”“减1”，还是不加不减。笔者认为，植树问题的教学不是归纳出三种类型，将它们加以记忆甚至要求学生以此为模板对号入座那么简单，而是要遵循数学广角的设计理念：经历数学学习的过程，在活动中感悟数学思想。

一、追本溯源，探究植树问题的“根”

植树问题承载的数学思想是对应，教学时应该充分发挥学具、图示的作用，让学生深入理解算式的意义、将学习目标牢牢定位在对应思想的体验与感悟上，真正建立“棵数”与“段数”之间的一一对应关系。这样，哪怕日后遗忘了所谓的公式，学生也能凭借对除法意义的理解，应用对应思想重新找回解决问题的路径与手段。这便是学习数学广角的意义与价值所在。

“植树问题”并非是一种横空出世的新问题，它与“路灯问题”“楼梯问题”“敲钟问题”“锯木问题”等都属于间隔问题，即间隔长度不变，点和间隔依次重复出现的问题。其中，间隔数＝总长度÷间隔长度，就是在求“一个数里面有几个另一个数”。因此，植树问题本质上是包含除意义的生活应用。教师完全可以将它与以前学过的用除法解决问题联系起来：间隔数就相当于“段数”，是除法运算得到的商，而植树问题求的是“棵数”，所以不能直接把商作为结果，还需要根据实际情况对商进行微调。就像有余数除法要根据实际情况对余数进行“进一”“去尾”的处理一样，植树问题的结果会出现“商+1”“商-1”“商不加不减”这三种情况。

二、求简重悟，实践植树问题的“本”

基于对植树问题本质属性的判断，根据它的教材定位，结合它的教学现状，笔者以为：既然植树问题本质上是除法，那就从包含除入手，把它定位成特殊的除法问题进行处理；既然数学广角定位在数学思想的感悟，那么学生应用一一对应思想成功解决问题的经历便是本课最大的价值。为此，笔者求简重悟，进行了以下的教学实践与创新。

（一）循序感悟，完善活动经验积累

植树问题作为特殊的用除法解决问题，并非空降而来，自有其来龙去脉。静心回溯，抬眼便见蕴伏，比如：

（1）一个一个数，从3数到8，要数几次？

（2）画一条5厘米长的线段，从刻度3出发，要画到刻度几？

（3）爸爸出差，3月3日出发，3月8日回来，一共去了多少天？

以上3题都是数学学习中的常见问题，看似风马牛不相及，其实就是间隔问题的雏形与生活原型，是系统学习植树问题的基础。如果将其转化成线段图，其共有的本质就呼之欲出。

这里的数次数，计算经过的天数，就是“棵数”，而画线段是单位长度的累加，关注了“段数”。类似的题还有很多，且都有相应的变式。这些从一年级开始就逐渐出现在我们眼前的学习材料，都是感悟植树问题的良好载体，需要教师用足用好。如通过画一画、数一数、比一比等活动积累基本的数学活动经验，以期厚积薄发，本课亦不例外。

【课堂回眸】

1.情境呈现。

师：在一条长20米的小路一边植树，每隔5米种一棵，需要种几棵？请你在练习纸上画一画，再列式算一算。

2.反馈汇报，整理验证三种情况。

（1）两端都种。

黑板上学具验证，突出间隔5米。

（2）只种一端。

师：生活中什么情况下这一头就不种了呢？（有障碍物）

师：障碍物还可能在哪里？（突出首尾）

师：能不能中间不种？（排除非间隔问题）

（3）两端不种。

3.小结。

师：看来在同样的条件下，生活中会出现这样三种情况。

【片段分析】

通过画一画、算一算，学生能整体感知植树问题的三种情况，了解生活中由于实际情况的不同，植树的结果也会不同。这三种情况中，只种一端的情况需深入解读。“可以头不种，可以尾不种”，那学生自然会想到能不能中间不种，但中间不种的情况恰恰不是正解，从表面上看，不符合“每隔5米”的条件，从本质上说，就不属于间隔问题，看似随口一问、顺手一解，其实是对今天所研究问题的概念界定。

（二）另辟蹊径，纳入原有知识体系

植树问题的本质是间隔问题，归属于用包含除解决问题，只是要根据具体情况对商进行微调。因此，教学可以从除法入手，与除法的意义建立关联，将其纳入学生原有的认知结构。

【课堂回眸】

1.回顾旧知。

师：课前，同学们编了能用20÷5=4解决的数学问题，如：20个桃子，5个一筐，能装多少筐？每盒牛奶5元，20元能买多少盒？想一想，为什么讲的事情不一样，却都可以用20÷5=4来解决？

生：都是在求20里面包含了4个5。

2.新课学习（略）。

3.对比提升。

师：刚才我们研究了植树中的数学问题，一起来回顾一下，明明是同样的信息，为什么会出现不同的结果？

生：考虑生活实际，情况不同，答案也不相同。

师：答案不一样，那有什么一样的地方吗？想一想，都是先求什么？

生：都是求段数，用除法。

师：为什么要用除法来算？

生：都是求20里面有几个5。20米中，5米一段，有这样的4段。

师：4段要种几棵树呢？

生：要根据生活实际来考虑棵数。如果是两端都种，一棵一段，多出1棵要加1；如果只种一端，一一对应，不加不减；如果两端不种，少了1棵要减1。

师：植树问题和学过的除法有什么不同呢？

小结：植树问题本质上就是除法问题，要根据实际情况对答案进行调整。

【片段分析】

课堂伊始，教师出示了学生用20÷5=4编写的数学问题，在这里有意识地选择了包含除，目的是唤醒学生的认知，同时也为后续与植树问题进行比较备好素材。对比提升环节，教师通过问题串的形式引发学生深入思考。“同样的信息，为何结果不同？”指向植树问题的现实背景，“答案不同，有相同的吗？”意在发现它们的共通之处，“为什么用除法做？”揭示它的除法本质，“4段要种几棵？”关注了对商的处理。层层递进，串珠成链，引导学生将今日新知纳入原有的知识体系，求同存异。

（三）图式结合，切实体验一一对应

学习植树问题的关键，是用“一一对应”的思想来分析两个量之间的数量关系，完成从“段数”到“棵数”的转化。因此，结合图示理解算式的含义，通过对应建立两个量之间的关联，是本课的重点也是难点所在。

【课堂回眸】

1.两端都种。

（1）理解算式的含义。

师：种了几棵，你能用算式来表示吗？生：20÷5＝4，4+1＝5。

师：20÷5＝4，这个4表示什么？

生：有4段，也就是20里面有4个5。

师：为什么要加1？结合图给我们解释解释。

生：一棵树对应一段，右边多出一棵要加1。

结合学具进行操作（如图）。

师：这两个4一样吗？

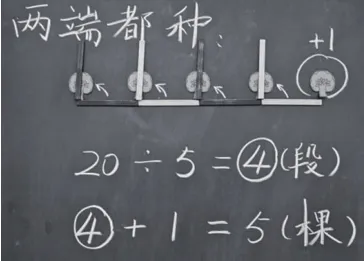
生讨论后得出结论：不一样，第一个4表示4段，第二个4表示和4段一一对应的4棵。

（2）探寻解决方法。

师：（课件呈现）如果接着往下种，25米要种几棵？怎样的6棵？

生：和5段一一对应的5棵，和一一对应后多出来的1棵。

师：（课件呈现）100米呢？

师：看着屏幕和黑板，如果两端都种，怎么求棵树？

生：棵数＝段数+1。

2.只种一端与两端不种。

师：只种一端和两端不种的情况下，棵数和段数又有怎样的关系？为什么是怎样的关系？选择一种，和同桌一起画画图，讨论讨论。

【片段分析】

20÷5＝4，4+1＝5，这两个“4”是同样的意思吗？一开始，学生可能会发愣，但很快就会有所顿悟，在对比中发现第一个“4”作为除法的商，求的是“一个数里面有几个另一个数”，是“段数”，而第2个“4”则是“棵数”，进而思考“段数”是如何与“棵数”建立联系的。通过学具的操作摆放，深刻体会“一一对应”正是解决这个转化问题的关键所在。因此，关注到两个“4”的区别，就关注到了两个量之间的关系，就找到了体验植树问题背后数学思想的抓手。

三、学以致用，寻找植树问题的“形”

植树问题很多时候并未清晰告知类型，是隐藏了提示语的，给学生的学习带来巨大困难，“上课热热闹闹，作业乱七八糟”也就能理解了。教学时需要引导学生透过现象看本质，寻找生活中植树问题的应用范例，让学生能够用学到的“植树问题”的原理来解释生活中的现象，充分感受数学与生活的紧密联系。为此，笔者进行了三个层次的练习设计。

（一）简单应用重对应

师：先判断下面的3件事分别属于哪种情况，再列式计算。

（设计意图：基础练习提供了植树问题的常见范例，具有典型性，将学生从“树”的定势中解脱出来。练习时重在引导学生结合实际情况展开判断，对商的结果进行调整。）

（二）提升练习会联想

师：这是宁波地铁分布图，请你当当小小设计师，为规划中的地铁线路设计站点。

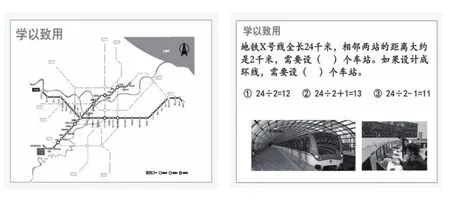
（1）直线型。

师：为什么是两端都设站点？

（2）环形。

师：环线是什么意思？其实就是哪种情况？你能想办法证明吗？

课件播放从环线到一端不设站点的变化过程。

（设计意图：提高练习结合社会热点，渗透环形的情况，并通过课件，演示了与“只种一端”之间的关联。这一做法既再次突出了“一一对应”思想，也促进学生进行知识间的联想。）

（三）拓展练习促深思

（1）101班正在进行优秀年画展示，展出了6幅作品（如图固定）。一共需要多少个磁铁？（3+1）×（2+1）＝12（个）。（2）依然照这种方法固定，要展出12幅作品，最多需要（）个磁铁？

（设计意图：无论是直线型还是环形，都是一维平面上的植树问题，拓展练习将这一问题推向二维，学生需要从长、宽两个角度进行思考，颠覆了学生的惯性思考，那还能不能推广到三维呢？想必深思的种子会就此生根发芽、深入人心。）