观察,需要的不仅仅是仔细
□ 王广科
观察是一种有目的、有计划、比较持久的知觉活动。观,不仅是看,还包括听、触等感知行为,察是分析思考,观察是多种感官的综合感知,蕴含着积极的思维活动。巴甫洛夫在他的研究院门口的石碑上刻下了“观察、观察、再观察”的名句,以告诫他的学生:没有好的观察能力,就没有科学发现。史宁中说:要学会用数学的眼光观察现实世界。数学观察是学生应该具备的关键能力之一。在教学中,我们经常发现,学生不会观察,往往是观而不察。在教学时,教师也很少指导学生进行有效的观察,只是一味地给学生提出“要仔细看”等态度上的要求,学生的观察能力没有得到相应的提升。观察,需要的不仅仅是仔细。在态度之外,我们还要关注学生观察能力的提升。
一、观察需要系统比较
探索规律是小学数学教学的重要内容。在教学中,我们往往是领着学生从简单入手,列举出三四个例子,让学生从中发现规律,进而借助规律解决问题。简单地说是“举例子—找规律”。找规律并不容易,不是有了例子规律就能自然出现,没有“系统的观察比较”,很难发现其中的规律。比如下面的问题。
问题1:如下图,摆1个三角形用3根小棒,增加1个三角形,多用2根小棒……摆10个三角形用( )根小棒,摆n个三角形用( )根小棒。

为了提升学生的观察能力,在教学中教师给学生总结了“左右看变化,上下看关系,数形结合看道理”的系统观察要求。先让学生在图形下面有序地写出“序号、结果与算式”。

左右看变化:重点看结果。3,5,7,9……很容易发现,每增加1个三角形,就多用2根小棒。
上下看关系:重点对算式与序号做比较观察。容易发现,增加的2的数量比三角形个数少1。摆10个三角形需要多少根小棒,就可以用3+(10-1)×2=21根小棒。摆n个三角形需要多少根小棒,就可以用3+(n-1)×2这个式子来表示结果,化简后得2n+1。
数形结合看道理:重点是把“含有字母的式子与图形相结合”进行深入比较。为什么是2n+1呢?能不能结合图形说一说其中的道理?引导学生发现:可以把第一个三角形也看作用2根小棒,这样每个三角形就都用了2根小棒,所以用2n来表示,再加上少看的一根,也就是(2n+1)根小棒。
得到2n+1后,我们还可以进一步观察含有字母的式子与结果的变化规律,还能惊奇地发现,相邻两数递增几,含有字母的式子中n就乘几。这当然不是巧合,同样可以结合算式进一步观察出其中的道理。有了这样深入系统的比较观察,学生在解决同类问题时,就可以直接根据结果写出含有字母的式子。
上述方法,给了学生“观”的角度:上下、左右、数形,引导学生进行有顺序的全面观察;也给了学生“察”的方法:看变化、看关系、看道理。这样一来观察就有了抓手,学生的观察能力就会逐步提升。
二、观察需要聚焦核心
聚焦,在物理上指的是控制一束光或粒子流使其尽可能会聚于一点的过程,在写作上是确立文章焦点的写作手法,在数学上是把目光和思维集中在能够展示重要数量关系的关键图形和关键位置的做法。当我们遇到条件过多、信息复杂而干扰学生思考的问题时,就需要进行聚焦式观察,寻找核心条件,剥离出基本图形,进行深入观察,从而寻得其中的数量关系和解决问题的思路。比如下面的问题。
问题2:如图是由风筝形和镖形两种不同的砖铺设而成的。请仔细观察这个美丽的图案,并且回答风筝形砖和镖形砖的内角各是多少度?
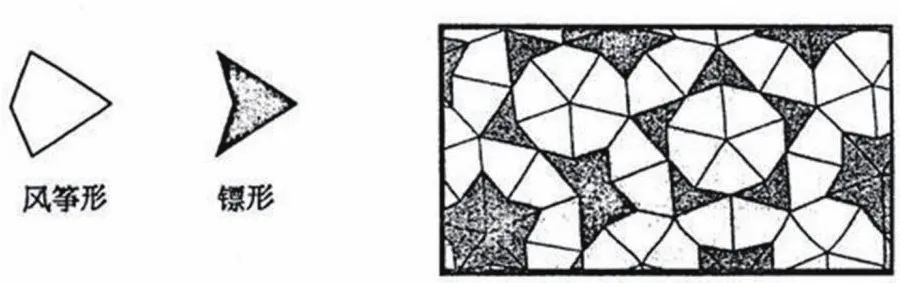
直接观察原图,“美丽”变成负担,复杂形成困扰。这时就需要进行“聚焦核心”式的观察。引导学生从上面的复杂图形中剥离出基本图形:正十边形,根据正十边形的内角和公式,很容易得出风筝形的4个内角度数:72°,72°,144°,72°。解决完风筝形的问题,可以借助风筝形研究镖形的各个角度,这时又要把目光聚焦在两种图形的相接处,如下图所示。

借助第二次的聚焦,也能够顺利地算出镖形各个角的度数:72°,36°,36°,144°。对学生来说,解决问题的困难不是基础知识的有无多寡,而是聚焦式观察能力的强弱。聚焦式观察可以将复杂问题转化为基本问题,实现化难为易、化繁为简的目的。在教学时,剥离出基本图形,聚焦关键区域,教师不能直接指出,也不能好心地给出聚焦后的简单图形。教学的目的不是“题目听得懂”,而是把“方法带得走”。“聚焦式观察”要从教师的素养转化为学生的能力。因此,在教学中教师要有意识地引导学生形成主动聚焦的意识,培养学生敏锐捕捉关键图形的能力,帮助学生从无所适从的浏览走向聚焦式的深入观察,让聚焦观察成为学生的习惯,进而提升学生的数学素养。
三、观察需要动态想象
在数学上,观察对象多是静态的图形,仅仅进行静态观察难以发现数量之间的关系,难以寻得解决问题的思路。观察需要调动想象,想象作图的过程,想象动点移动时图形的变化。借助纸上之图,形成脑中的动态图形,可以有效地区分主要条件和次要条件,把握不变量,巧妙地解决问题。比如下面的问题。
问题3:如下图1所示,在腰长为10厘米,面积为34平方厘米的等腰三角形底边上任意取一点,设这个点到两腰的距离分别为a厘米和b厘米,那么a+b的长度之和是多少厘米?

图1
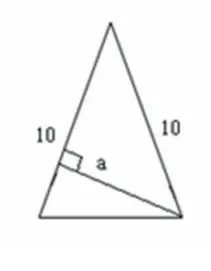
图2

图3
直接观察原图,我们很难找到思路。当我们关注到“底边上任意取一点”这一信息时,就可以在大脑中展开动态想象,将底边上的点沿着底边做左右移动,在移动的过程中,定格在两个特定位置:顶点和中点,观察这两个特殊位置(如图2、图3),我们很容易算出,a+b的长度之和是6.8厘米。这样做,不仅仅是为了更快地寻得答案,更重要的作用在于:随着动点的移动,我们可以感受到,a和b的长度不断变化,变化方向是相反的,图3分割线两边的面积不断变化,变化的方向是相反的,这种相反方向的变化就会让我们自然地联想到“面积和不变,两条高的和也不变”,抓住了变化中的不变关系,就容易想到整体思考的策略。连接图1中等腰三角形的顶点和底边上的任意点。进而列出方程:10a÷2+10b÷2=34,化简后得到:5a+5b=34,将a+b看作一个整体,求得:a+b=34÷5=6.8。整体思考这一思路的获得,不是教师直接给予的,而是来自“动态观察”。“动态观察”在几何问题中经常出现,有着十分重要的作用。比如多边形的外角和是360°,将多边形动态缩小至一个点即可看出多边形的外角和都是360°。将圆转化成长方形,要对切拼后的图形进行动态想象:随着均分小扇形份数的增加,底边越来越直,半径逐渐和底边垂直。
如何提升学生动态观察的能力?可以要求学生在纸上重新绘图,体会画图的步骤与过程;还可以引导学生寻找“可移动的点、线、面”,借助想象对点、线、面做动态处理,从中感悟数量之间变与不变的关系。让图形在学生的眼中活起来,以动态的“观”促进巧妙的“察”。
综上所述,观察需要的不仅仅是仔细,还需要方法,需要适时的启发,需要细致的指导,需要长期的培养。苏霍姆林斯基说:观察是智慧最重要的能源。从观察中不仅可以汲取知识,而且可以让知识活跃起来,知识借助观察而“进入周转”,像工具在劳动中得到运用一样。如果说复习是学习之母,那么观察就是思考和识记知识之母。让观察成为学生的一种能力,怎一个“仔细”了得?对一线教师来说,可谓任重道远,但只要多维并举,持之以恒,亦能得始终。

