几何直观在代数领域的构造与运用策略

□ 胡良梅

儿童学习数学的主要矛盾是抽象和形象的矛盾，几何直观是化解这一矛盾的有效措施。何为“几何直观”？《义务教育数学课程标准（2011年版）》指出：“几何直观主要是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”几何直观，本质是借助直观图形获得感性认识，描述、分析、理解问题，几何直观是种意识，是种思维方式，也是教学手段，它的主旨是加深学生对数学的理解，它存在于数与代数、图形与几何、统计与概率等数学学习的各大领域教学中。

在代数领域，几何直观怎样才能发挥更广的价值？教师可积极寻找数学对象的直观模型，构造易于理解和运用的直观形式，努力发挥几何直观的价值。现举例分析如下。

一、画出数的特征，揭开特征的面纱

小学阶段，认识自然数、分数、小数，都是通过大量使用几何直观，如小棒图、数珠图、算盘图、立方体模型图、面积模型图、特殊米尺图等来完成的。除去教材编写的这些几何直观，教学中还可以怎样构造直观呢？

（一）逆向拓展，构造直观

教材编排认数的逻辑顺序一般是：直观图—数珠—数的符号，学生经历的是从具体数量逐步抽象，并用数学语言进行表达交流的过程。其实，还可以反其道而行之，引导学生经历从抽象到具体的构造直观的过程。如用不同图示画出一个数：10表示什么意思？你能画图表示吗？学生可以画出10朵花、10根小棒、10个圆圈等具体情境图，也可画出1捆小棒、1个直条长方形等比较抽象的直观图。接着，教师出示：8个大大的圆圈图和2个非常小的圆圈图，问：这幅图能用10表示吗？强烈的大小反差，冲击着学生的思维，有学生认为不能。经过辩论，最后明确大小虽不同，但不影响数量的表示，这就加深了学生对数字10抽象意义的理解。之后，教师可再追问：与前面学习的0～9相比，10有什么不同？你能画图说明吗？学生想到用计数器图表示10占有两个数位，并且发现10已经不再用新的数字计数，是用已学过的1和0计数……在这个创造图示并区分、拓展的思维经历中，有抽象素养的自然孕伏，还有伟大的十位进制原理的体验，学生历经了数的概念的理性认识过程，思维能力切实得到了提升。

（二）深入组成，构造直观

知道数的特征是什么，还要理解数的特征为什么，才能揭开特征的面纱，促进学生的深度学习。如2，5倍数的特征，为什么只要看个位？3倍数的特征，为什么要看各个数位上数字相加的和？用直观图示画出数的组成，可促进学生知其然并知其所以然。

看图可直观理解：多位数是整百整十和个位数合成的，前面的整百整十确定是2，5的倍数，所以关键看后面的个位。并且，个位数除以2或5得到的余数，与多位数除以2或5的余数具有一致性。3的倍数特征也同样可以这样构造直观，促进理解：245÷3=（200+40+5）÷3，一个百除以3会余1，2个百除以3就余2……几个百除以3就余几；一个十除以3会余1，2个十除以3就余2……几个十除以3就余几。（图略）

二、画出运算方法，理解算法的意义

整数、小数、分数的四则运算，也在一直使用几何直观。如整数的加减乘除，离不开小棒图、点子图的拆分组合，分数乘法的计算离不开直观图的探索理解等。那么，在数的运算学习中，又该如何引导学生去主动构造几何直观呢？

（一）材料促思，构造直观

除法竖式的理解，一直是学习的难点。如教学92÷30时，部分学生会认为商是30，如果简单否定，或是单纯依靠正面示范和反复练习，效果不尽理想。这时，可引导学生主动构造直观：给学生提供方格纸，让学生借助直观的格子图圈一圈、画一画，再通过交流和追问，学生就会结合直观模型“自我否定”，完善认知建构，形象理解商和余数的意义。一些特殊的、复杂的、抽象的运算，也可引导学生主动构造直观探索简便算法。如：，教师提供长方形纸片、圆形纸片或者数轴图，让学生折一折、画一画、标一标，借助操作与图示，大多数同学都能领悟这道计算题可以化繁为简，转化为显然，这是几何直观的神奇价值。

（二）模型引路，构造直观

分数除以分数，苏教版教材分三步进行：分数除以整数—整数除以分数—分数除以分数。从平均分升果汁—平均分4个橙子—包含分4米长的彩带—包含分升果汁，素材选取的都是同类量的分一分，比较单一，学生因此形成的理解也比较肤浅。为了丰富分数除法的数量关系，加深学生对算理的理解，可增设素材，构造不同的直观模型。如一辆汽车行千米用汽油升，1升汽油可供这辆汽车行驶多少千米？画出的计算过程。

三、画出数量关系，明晰解题思路

很多实际问题中的信息和数量关系都是可以画出来的。从低段教学开始，可以先试着画直观形象的示意图、直条图、线段图，到了高段，还可以适时引进矩形图、韦恩图等。

（一）于题意混淆处构造示意图

如乘加对比实际问题，部分学生往往混淆不清，类似下图这样的题目就可以引导学生画示意图帮助理解。也可以改为：姐姐送给弟弟9枚邮票后，两人邮票的枚数同样多。原来姐姐比弟弟多多少枚？学生往往易理解为姐姐比弟弟多9枚。可先指导学生画实物示意图帮助理解，再改动小数字为大数字，体验示意图的局限性，逐步抽象出直条图、线段图。

（二）于题意不明处构造矩形图

苏教版四年级下册“解决问题的策略”，重点编排了线段图和矩形图。如：扩建校园时，一个正方形操场的一组对边各增加18米，操场的面积就增加了900平方米。原来操场的面积是多少平方米？其中“一组对边各增加18米”学生不明白是什么意思，可借助直观的矩形图帮助分析，理解其中的数量关系。其实，矩形图除了用于面积，还可迁移到更广的范围。如同类数量关系的直观揭示、方法多元的思路寻求等。例如：美术小组计划买20盒彩笔，每盒15元。实际每盒涨价3元，且多买5盒，实际多花多少元？图中阴影部分就是多花的钱，借助矩形图的直观构造，可以探索不同的解题思路。

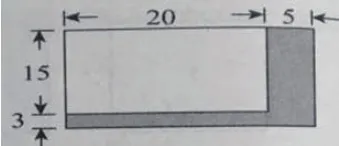
（三）于数量隐蔽处构造韦恩图

如大家都熟悉的包含问题：一个班有35人，老师问：做完语文作业的请举手。有18人举手。又问：做完数学作业的有几人？请举手。有21人举手。最后问：语文和数学作业都没有做完的同学有吗？没有人举手。请问，语文和数学作业都完成的有几人？题中的数量关系比较隐蔽，部分学生会觉得很难理解。如果能够帮助学生构造几何直观，就会非常清楚。

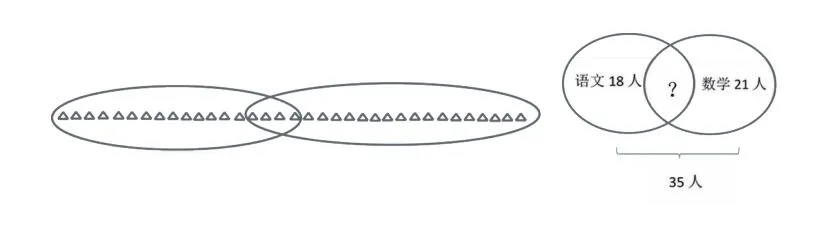
先画出一个班的35人，从左边数18人是完成语文作业的，圈一圈；从右往左数21人是完成数学作业的，再圈一圈。借助直观图很容易看出重叠的4人就是既完成语文作业又完成数学作业的人数。进一步，还可以逐步抽象出韦恩图。

（四）于关系复杂处构造线段图

小学高段的实际问题往往数量关系复杂，为了化繁为简，化隐为明，教师可指导学生积极构建线段图。如，学校要组织两组队员去牡丹园春游。牡丹园距离学校有15千米，比较远，并且学校只有一辆校车，每次最多只能容纳一组的学生。假如车速每小时48千米，步行速度保持每小时4千米，请问，两个小组怎样轮流乘车，才能保证最短时间内同时到达？读完题目，似乎无从思考，不妨构造线段图帮助分析。思考：校车从A点出发，先把第一小组送到C点，立刻回头刚好到B点接送第二小组，最后两个小组一起到达D点牡丹园。为了保证公平，两个小组步行路程相同，即AB=CD。因为车速是步行速度的12倍，把AB路程看作1份，相同的时间内，校车行驶的路程就是12份，即BC之间的路程就是（12-1）÷2=5.5份。由此得出每个小组步行的路程是15÷（1+5.5+1）=2千米。

借助直观的线段图帮助分析，数量关系明晰可见，问题迎刃而解。其实，许多复杂的行程问题都可构建线段图简明数量关系。再如比较经典的年龄问题：徒弟问师傅今年多少岁？师傅说：“当我像你这么大时，你才5岁；当你像我这么大时，我已经71岁了。”师傅今年多少岁？此题表达虽简单，只告诉了两个量，但内涵丰富，理解起来颇有难度。不过，依据题意，抓住年龄差不变，画出线段图，就可以转化成容易解答的差倍问题了。如右图，可以直观看出，师徒之间的1个年龄差是（71-5）÷3=22（岁），师傅今年的年龄是5+22×2=49（岁）。

此外，在探索规律、常见的量、式与方程等的学习中也可积极创建几何直观。

如0.1小时和0.1元的理解，学生往往会认为0.1小时就是10分钟。引导学生借助数轴画出直观图，就能帮助学生形象理解钟表上的小数：因为钟表用的是60进制，60÷10=6分钟，0.1小时就是6分钟；而“元、角、分”用的是10进制，0.1元=1角，所以就不一样了。

当然，自觉运用几何直观，形成几何直观的意识，离不开灵活运用中的成功体验。因此教师要引导儿童经常性地构造几何直观，并常常反思体会几何直观的优势，要有意识地培养儿童的几何直观意识与能力，帮助儿童逐步形成一种“遇抽象画形象”的稳定的思维方式。当然，构造几何直观之后，还需要重点关注几何推理、直观洞察的思维发展。此外，在图形与几何、统计与概率等数学领域，我们也要进行深入研究，丰富实例，逐步形成几何直观的构造系列。