四则运算之“序”的教学之“理”*
□ 徐宏臻
一、缘起
学校举办赛课活动,内容是苏教版四年级上册第七单元的“整数四则混合运算”例1(主题图如图1)。笔者发现,许多教师在引导学生分步列式的基础上,启发学生结合事理和数量关系列出综合算式12×3+15×4或 15×4+12×3,并确定先算什么,后算什么,最后算什么。许多教师教完例1后,就引导学生总结出混合运算的顺序规则:在没有括号的算式里,有乘、除法和加、减法,要先算乘、除法,再算加、减法。
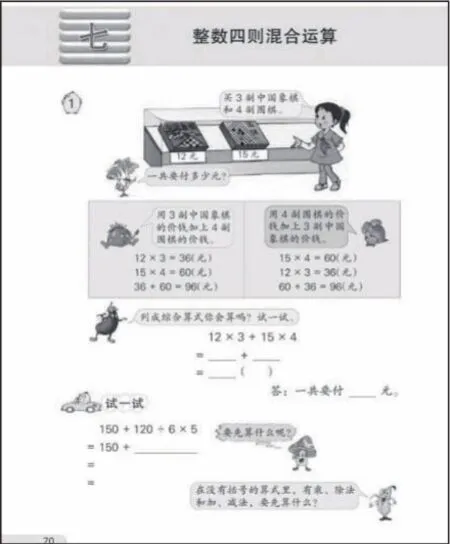
图1
接着教学“试一试”。“试一试”是计算150+120÷6×5,教材旁白:要先算什么呢?学生根据例1得出的运算顺序规则,容易说出:在没有括号的算式里,有乘、除法和加、减法,要先算乘、除法,再算加、减法。可是,紧接此后,教材又要求学生归纳和总结没有括号的混合运算式题的运算顺序。明明教师在教学例1时,已经得出了混合运算的顺序规则,并且在“试一试”时又用到了这一规则,为什么教材这时又要求学生归纳和总结这一规则?教师这样教是不是逻辑混乱、循环论证?评课时笔者提出这一问题,在场的三十多位教师无人答得上来。
无独有偶,在另一次“同课异构”教学中,笔者又听了两节这样的课,其中一节课同上所教。另一节课则在上课伊始,就通过复习三年级的混合运算顺序,诸如200+100×5,200-100÷5等,引导学生得出上述混合运算的顺序规则。接着,就让学生直接运用这一规则进行计算。那么,执教者是否思考过教材编排的序及其逻辑联系,究竟怎样让学生理解规则内在的“理”?
二、找序

图2
苏教版教材“混合运算”一词首次出现是在三年级下册第四单元,用三道例题教学“混合运算”,例1见图2。教材联系学生非常熟悉的购物情境,引导学生根据所求问题,列出数量关系式:3本笔记本的钱+1个书包的钱=一共要用的钱,或1个书包的钱+3本笔记本的钱=一共要用的钱。数量关系式极为重要,因为它指导着学生列分步算式和综合算式及如何对综合算式5×3+20或20+5×3进行计算,明确先算什么,再算什么,知道两式都要先算乘法。在此基础上,教师再引导学生归纳和总结出一条有关混合运算顺序的规则:算式中有乘法和加、减法,应先算乘法。值得提出的是,混合计算只涉及三个数。
接着呈现例2(见图3)。同样在依据数量关系的基础上,列出综合算式,并得出另一条有关混合运算顺序的规则,即算式中有除法和加、减法,应先算除法。最后例3教学有括号的算式的运算顺序,列出综合算式,并得出第三条混合运算顺序的规则:算式里有括号,应先算括号里面的。

图3
可见,三年级下册教材并未归纳出“先乘除,后加减”这一规则,也没有把乘、除法与加法混合在一起,或把乘、除法与减法混合在一起,更没有把乘、除法与加、减法同时混合在一起。执教老师课前没有理清教材编写的“序”,想当然地超前了,把新知当成已知看待了。
苏教版教材是在四年级上册才进行综合的(图1)。教材用一道例题引入四个数的混合计算,如12×3+15×4,借助数量关系式,说明乘、加法混合仍然要先算乘法,再算加法,与三年级一样。这时,教材并未要求学生归纳出混合运算的顺序规则。接着,通过“试一试”,即计算150+120÷6×5,把乘、除法与加法混合在一起,并引导学生思考:要先算什么呢?引导学生根据已有的知识和经验,类推出要先算乘、除法,再算加法,而这里乘、除法混合在一起,要按照从左往右的顺序进行计算。在此基础上,再引导学生归纳和总结出混合运算的顺序规则:在没有括号的算式里,有乘、除法和加、减法,要先算乘、除法,再算加、减法,即“先乘除,后加减”,原来如此!
三、明理
没有括号的四个数的混合运算该怎么教,才能体现教材编写的“序”,又能让学生理解规则内在的“理”呢?请看以下教学片段。
【教学片段】
1.激活已知
分别说出下列各式的运算顺序:200-100+50,200÷100×50,200+100×50,200-100÷50。
待学生准确说出顺序后,引导其回忆:算式中只有加、减法或只有乘、除法,要按从左往右的顺序进行计算;算式中有乘法和加、减法,应先算乘法;算式中有除法和加、减法,应先算除法。
[设计意图:课始复习三个数的混合运算有利于激活学生已有的知识和经验,为学习新知奠基。]
2.探明算理
我们知道了无括号的三个数的混合运算的计算顺序,那么,如果是四个数的混合运算,该按怎样的顺序进行计算呢?今天这节课我们就研究这个问题。
(1)出示主题图(如图1),引导学生说出条件和问题。
(2)引导学生依据事理说出并板贴下列数量关系式:3副中国象棋的价钱+4副围棋的价钱=一共要付的钱;4副围棋的价钱+3副中国象棋的价钱=一共要付的钱。请大家算一算。
(3)交流反馈。
①展示分步列式,并让学生依据上述数量关系式说出理由(过程略)。
②有列综合算式的吗?根据学生的交流,教师板书12×3+15×4,15×4+12×3。让学生思考:在计算12×3+15×4时,应该先算什么,再算什么,最后算什么,教师板书12×3+15×4=36+15×4=36+60=96(元)。同样,在计算15×4+12×3时,学生思考:应先算什么,再算什么,最后算什么,教师板书15×4+12×3=60+12×3=60+36=96(元)。有学生把两个乘法算式同时计算,即12×3+15×4=36+60=96(元),则让学生通过对比感悟到:在算3副中国象棋的价钱时,并不影响算4副围棋的价钱,而且这样计算更简洁。
接着,教师让学生观察算式15+15+15+15+12+12+12,思考:如果要求这7个数的和,你认为怎样算快些?学生普遍认为,先把4个15相加的和与3个12相加的和分别算出来,再把这两个和相加,这样快。于是,教师板书15+15+15+15+12+12+12=15×4+12×3。让学生对比等式左右,明确在计算15×4+12×3时,应先算相同加数的和,即乘法。
笔者顺势引导学生把15+15+15+15-12-12-12改写成15+15+15+15-(12+12+12)=15×4-12×3。学生发现,在计算15×4-12×3时,同样应先算乘法,再算减法,即15+15+15+15-12-12-12=15×4-12×3=60-36=24。
(4)小结。观察12×3+15×4、15×4+12×3、15×4-12×3的计算顺序,说说算式中有乘法和加、减法时,应先算什么,从而总结得出规则:算式中有乘法和加、减法,应先算乘法,与三个数的混合运算一样。
[设计意图:从现实生活中找原型,紧扣数量关系式,引导学生分步列式和列综合算式,同时依据数量关系式确定和理解混合运算的顺序。在此基础上,为了让学生从算理上进一步理解混合运算的顺序规则,让学生观察等式15+15+15+15+12+12+12=15×4+12×3,以及15+15+15+15-12-12-12=15×4-12×3,让学生从算理上明确先算乘法的合理性。]
(5)研究除法。买3副同样的中国象棋要用36元,买4副同样的围棋要用60元。每副围棋比每副中国象棋贵多少元?你能列出综合算式并算一算吗?
学生展示综合算式并述理,教师板书60÷4-36÷3。学生思考应先算什么,再算什么,最后算什么。因为在算每副围棋的价钱时,并不影响算每副中国象棋的价钱,所以两个除法可以同时算,即60÷4-36÷3=15-12=3(元)。由此引导学生发现:算式中有除法和加、减法,要先算除法。让学生练习计算60÷4+36÷3(略)。
[设计意图:例题列举了乘加的例子,没有列举乘减和除加(减)的例子,对小学生来说,要总结和概括混合运算的顺序规则需要较为全面的例子。]
(6)小结规则。引导学生回顾15×4+12×3,15×4-12×3,60÷4-36÷3和60÷4+36÷3的计算过程,说说它们在运算顺序上有何相同点,从而总结和概括出:算式中有乘法和加、减法,要先算乘法;算式中有除法和加、减法,要先算除法。
3.迁移运用
出示“试一试”。计算240+60÷6×5,引导学生整体观察和思考:应先算什么?学生说:根据前面的学习可知,乘法与加、减法在一起时,要先算乘法;除法与加、减法在一起时,要先算除法。因此这题应先算60÷6×5,再算加法,但这题乘、除法混在一起了,在先算60÷6×5时,要按照从左到右的顺序进行计算。因此,这题应先算除法,再算乘法,最后算加法。
学生计算并交流,教师要注意纠正学生的三种错误,并找出出错原因,让学生感悟到运算顺序的重要性。教师板书规范的计算格式(略)。让学生练习计算240-60÷6×5(略)。
观察240+60÷6×5和240-60÷6×5的计算过程,引导学生思考:一个算式里既有乘、除法,又有加、减法,应先算什么,再算什么?从而得出整数四则混合运算的顺序规则(略),这就是四个数的混合计算在没有括号时的运算顺序规则。
[设计意图:在学生得出乘加(减)、除加(减)算式的计算顺序基础上,让学生计算“试一试”,并说理,旨在让学生得出:在计算乘、除法与加、减法混合算式时,要先算乘、除法,再算加、减法。这样,学生对规则不但知其然,而且知其所以然。]
4.巩固练习(略)
教学中把三、四年级的教材有机地衔接起来,学生可以清晰地看到知识发展的脉络,感受到教材编写的“序”,同时学生能顺利地运用已知探明新知,把新知牢牢地“嫁接”在已知这根“桩”上,形成一棵“知识树”。这就是课标所说的:“数学知识的教学,要注重知识的‘生长点’与‘延伸点’,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性……”

