重视从“解题”到“解决问题”能力的培养

广东

随着高考命题改革的深入，高考数学秉承“多考如何想，少考如何算”的命题理念，越来越重视对考生数学思维能力的考查.从2019年数学高考大纲传递出的信息来看，预测2019年高考会把考查的重点转移到对数据的分析、理解和找规律上，减少繁杂的运算，突出对数学思想方法的理解和运用，注重对考生从“解题”走向“解决问题”的能力的考查.

在紧张的高考考前备考阶段，使复习取得事半功倍的效果，无疑是广大师生热切盼望的事.但问题在于，在高考临近的情况下，我们的教学将如何培养学生从“解题”走向“解决问题”的能力，使复习备考的成效更上一层楼呢？以下从三个方面谈谈认识，供老师们指导学生复习时参考.

一、突出“问题变式”，培养数学思维的深刻性

解决问题是高考数学的“主旋律”，在临考前的教学中，对一些典型试题，先来“解题”，然后引导学生进行变式，延伸出一类问题，从而走向“解决问题”，达到提高复习效率的目的.下面以一道《教学考试》杂志社优师计划项目研发试题为例.

( )

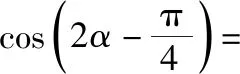
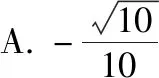
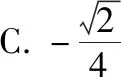
解析：本题是三角函数求值题，主要考查同角三角函数的关系、诱导公式和简单的三角恒等变换等知识.

解法1.因为tan(2 019π+α)=3，所以tanα=3.

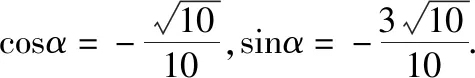
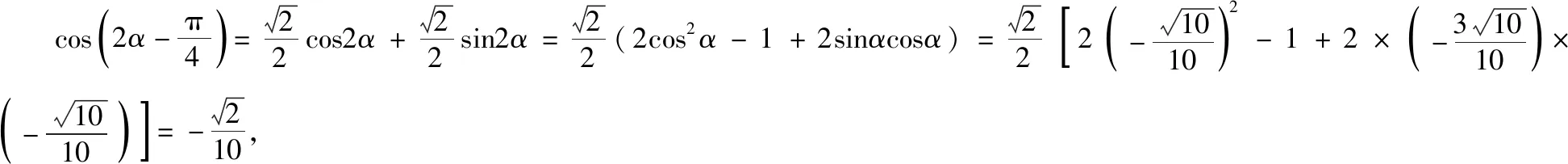
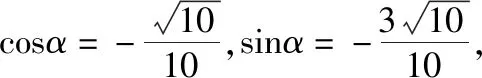
解法2.因为tan(2 019π+α)=3，所以tanα=3.

因为sin2α+cos2α=1，

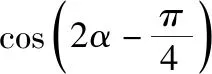
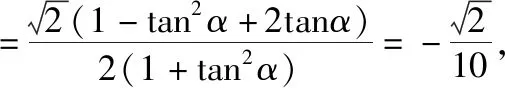
这样来看，解法2的计算量比解法1的计算量要小的多.不仅如此，我们通过解法2，还可以将题目的条件弱化，去掉“α是第三象限角”，便有下面的变式题.

( )

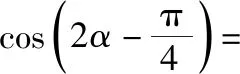
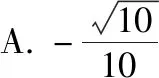
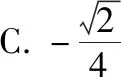
此变式真正体现出了“多考想，少考算”的高考命题思路.

由此我们可以提炼出这类问题的模型：已知tanα的值，求可化为关于sinα，cosα的齐次式的值.

以上过程很好地培养了学生从“解题”走向“解决问题”的能力.这样的教学给一道题带来的作用比刷数道题都要大.

二、重视“数学估算”，培养数学思维的敏捷性

“估算法”就是采用近似处理的手段来简化解决问题的方法，它实质上是一种数学思维意识，以正确的算理为基础，通过迅速、合理的观察、分析、比较、判断和推理，在众多信息面前，寻求出一些有用的或关键的数学信息，达到对问题进行判断、辨误、探索、导向、显隐、评价和优化的目的，从而使问题得到迅速地解决.“估算法”蕴含着数学抽象、数据分析、直观想象和逻辑推理等数学核心素养，是一种较高层次的数学能力.作为数学三大题型之一的选择题，由于其题型的特点，运用“估算法”有着得天独厚的优势.

因此，在高考备考的临考阶段，重视估算教学，加强运用数学估算法解数学选择题的基本对策的研究和方法指导，对培养学生的数学素养和创新能力颇有裨益.

( )

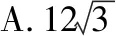
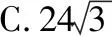
解析：本题以球与三棱锥的组合为背景考查空间几何体体积的计算，要明确球的截面性质，正确理解三棱锥体积最大时的情形.

解法1.三棱锥D-ABC的底面ABC位置确定时，高越大，体积越大，此时三棱锥D-ABC为正三棱锥.

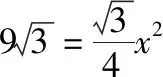
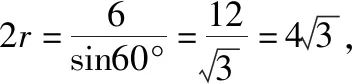
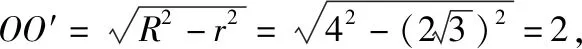
从“解题”角度来看，解法1值得称道.但这种解法需要首先求出等边△ABC的边长，再求△ABC外接圆的半径，进而根据球的截面性质求出三棱锥D-ABC的高，最后求得体积的最大值，计算量很大.所以从“解决问题”的视角来看，还远远不够.而下面的“估算法”可以弥补这点不足.

由此看来，“估算法”不仅是一种快速解题的方法，更重要的是与“多想、少算、快算”和“解决问题”的理念相契合.

三、强调“数学应用”，培养数学思维的广泛性

把高考内容与国家经济社会发展、科学技术进步和生产生活紧密结合，通过设置实际问题情境考查学生灵活运用所学知识分析和解决实际问题的能力，引导学生从“解题”走向“解决问题”是2019年高考命题的趋势之一，高考数学应用问题承载着这一重要“使命”，而概率统计应用问题则是良好的载体，且难度有增加的趋势.在高考命题中，应用题部分还将数据准备阶段的步骤减少，为考生呈现比较规范的数据格式或数据的回归模型.采取“重心后移”的策略，把考查的重点后移到对数据的分析、理解和找规律上，减少复杂的运算，突出对数学思想方法的理解和运用能力的考查，引导学生从“解题”到“解决问题”的能力的培养.

例3.(2018·全国卷Ⅱ理·18)如图是某地区2000年至2016年环境基础设施投资额y(单位：亿元)的折线图.

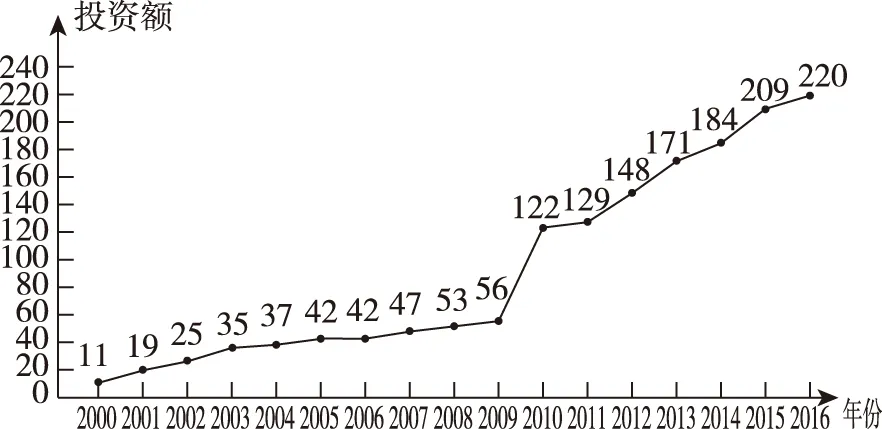
(Ⅰ)分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；

(Ⅱ)你认为用哪个模型得到的预测值更可靠？并说明理由.

解析：(Ⅰ)利用模型①,该地区2018年的环境基础设施投资额的预测值为

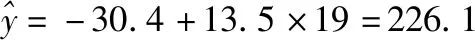
利用模型②,该地区2018年的环境基础设施投资额的预测值为

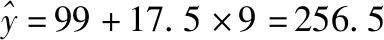
(Ⅱ)利用模型②得到的预测值更可靠.

理由如下：

(ⅰ)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=-30.4+13.5t上下.这说明利用2000年至2016年的数据建立的线性回归模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加，2010年至2016年的数据对应的点位于一条直线的附近，这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性回归模型②可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.

(ⅱ)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理.说明利用模型②得到的预测值更可靠.(数据分析)

以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.