对高考母题的整合与辨析

重庆

聚焦高考母题，对其实施“二次开发”——整合与辨析，搞好变式训练，能较好地体现一个人的思辨能力和思考的深度.要搞好同类试题对比研究和变式教学，那么师生就要在平常教与学中，注意收集与整合，辨析与提炼相关素材.这样一来，势必对学生的思维发展有利，对教学也会起到事半功倍的效果.下面我摘取一组试题来深度解读“整合与辨析”的思路，分享给大家，以便对学生的心智有所启发，仅供参考，不当之处，请予以批评指正.

一、对试题的整合与改编

例1(母题)(2013·全国卷Ⅰ理·15)设当x=θ时，函数f(x)=sinx-2cosx取得最大值，则cosθ=________.

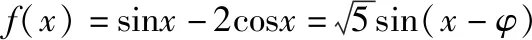
点评：思路1是通性通法，主要考查辅助角公式的运用.

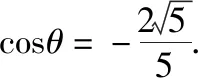
点评：思路2是导数在三角函数中的典型运用，但对符号的判断要求较高.

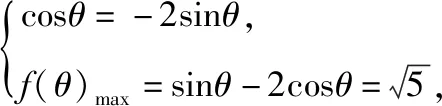
点评：思路3简洁明了，理解透彻,巧用“方程思想”解决问题.

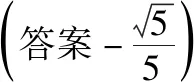
如果我们对例1进行适当改编，就可以得到以下2018年全国卷高考试题：

例2(母题)(2018·全国卷Ⅰ理·16)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是________.

思路1：注意到f(x)的最小正周期为2π，在[0，2π)内考虑最值.

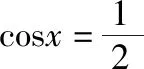
点评：由于函数有具体解析式，可以利用导数法求解.

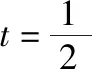
点评：同思路1，基本思路相同，只是适当采用了“换元法”.

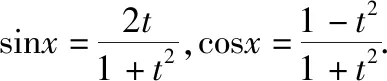
点评：现在的高中生对这种解法不熟悉，甚至可能不知道，可供有余力的同学学习.

思路4：(均值不等式)因为f(x)=2sinx+sin2x为奇函数，

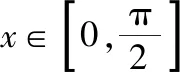
=2sinx(1+cosx)

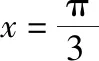
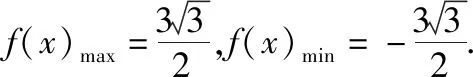
点评：这个要求学生的能力较高，对尖子生的选拔很有帮助.

思路5：因为f(t)=sin2t+2sint,令a=sint,b=cost，则z=f(a,b)=2ab+2a,约束条件a2+b2=1,构造拉格朗日函数L=2ab+2a+λ(a2+b2-1)(λ≠0),

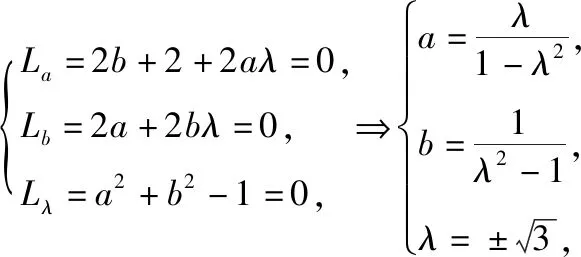
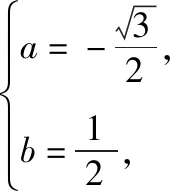
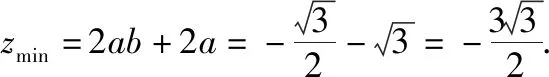
点评：本思路运用了高等数学背景知识，高中生掌握不了，但可以提供给他们，让他们感受数学方法的灵活多变，渗透给学生从不同角度解决问题的意识和理念.

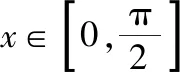
点评：本思路同思路5，运用了高等数学背景知识，高中生掌握不了，但可以提供给他们，让他们感受数学方法的灵活多变，渗透给学生从不同角度解决问题的意识和理念.

思路7：f(x)=2sinx+sin2x

=2sinx(1+cosx)≥-2|sinx|(1+cosx)

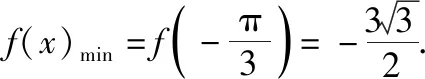
点评：本题先用了放缩法，然后利用了均值不等式解决问题，十分巧妙.

( )

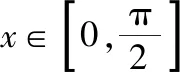
A.0 B.2

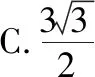
(读者可自行完成改编2，答案选C)

二、对试题的辨析与感悟

1.本文例1是针对y=asinx+bcosx(或y=acosx+bsinx)型研究其最值或值域问题，解题方法灵活，可以用辅助角公式法求解，也可用导数法求解，其中导数法解，思路3结合“解方程思想”，巧妙回避了思路2中判断符号的问题，显然是一种好方法.

2.本文例2是针对y=asinwx+bcosx(或y=acoswx+bsinx，或y=acoswx+bsinwx,w≠1)型研究其最值或值域问题，解题方法更加灵活，用到的思想方法有①数形结合法，②导数法，③换元法，④万能公式法，⑤均值不等式法，⑥构造拉格朗日函数法，⑦Jensen不等式法，⑧放缩法.虽然有些方法有高等数学的背景，但对学生的视野拓展是有利的.

3.这两个母题分别是2013年，2018年全国理科数学卷Ⅰ的高考试题.可以作为y=asinx+bcosx(或y=acosx+bsinx)型，y=asinwx+bcosx(或y=acoswx+bsinx，或y=acoswx+bsinwx,w≠1)型专题研究.在此基础上，可适当作出改编与拓展.

4.有了上面的铺垫，若将“+”改为“·”，那么我们再来看看，又有些什么感悟呢？

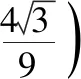
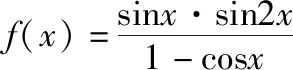
三、对试题的整合与辨析的反思