量子乘法器的设计及其实现方法

袁素真，王 艳，王玉婵，黄 斐

(重庆邮电大学 光电工程学院，重庆 400065)

0 前 言

20世纪80年代初， P. Benioff[1]首先提出了量子计算的思想；1982年，费曼[2]提出用量子计算机来模拟量子系统，其计算速度远超过经典计算机。现有的研究表明，量子计算以其并行计算的特性在一些领域里比经典计算有着很大的优势，例如信息论，密码学和图像处理等[3-7]。因为在量子计算机中，数据以量子叠加态的形式存储，而对量子叠加态的处理将同时对叠加态的每个分量进行，根据这个特性，可以将信息存储到叠加态的分量重，便于进行并行处理。也就是说，仅需要通过一次计算就可以得到函数f(x)在x处于不同值时的相应函数值。由于量子算法具有指数级加速部分经典算法的能力，被认为是解决当前物理系统计算能力瓶颈的有效手段之一。

量子乘法器是以更基本的量子加法器为基础，它可应用于量子图像处理中的滤波、边缘检测和频率控制等领域，设计快速高效的量子乘法器具有重要的意义。2014年，Kotiyal[8]设计了基于二叉树的量子乘法器，但其时间复杂度较高(即硬件复杂度)，为O(n3)。2017年，Hafiz Md[9]提出了一种高效的量子乘法器设计方案，利用乘数累加单元、量子全加器和量子“与”操作，实现了时间复杂度为O(n2)的量子乘法器。虽然文献[9]比前人所提出的量子乘法器在时间复杂度上有所提升，但其实现方法复杂。本文将提出一种结构简单的量子乘法器的设计方法，仅需要量子全加器和量子右移算子，其时间复杂度为O(n2)。

1 量子计算基础

1.1 通用量子门

对应于经典计算机中比特的概念，量子比特是量子计算机中存储信息的最小单元。一个量子比特，其一般形式为[10]

|ψ〉=α|0〉+β|1〉

(1)

(1)式中：α和β是复数，满足|α|2+|β|2=1；|0〉和|1〉状态称为计算基态。由此可见，n位经典比特只能表示2n个数中的一个，而n位量子比特可以表示为2n个数线性叠加的形式，也即对n位量子比特进行一次处理，等价于对2n个叠加项都同时进行了处理，这为设计高并行量子算法提供了理论基础。

经典电路是由包含连线和逻辑门的线路组成的，类似地，量子线路是由连线和基本量子门组成的。任意的多量子比特门都可以由受控非门和单量子比特门复合而成，某种意义上，受控非门和单量子比特门是所有其他门的原型。所以在这里仅介绍4个通用量子门：非(NOT)门、受控非(CNOT)门、哈德(Hadamard)门以及Toffoli门。图1为4个通用量子门的示意图。图1a的非门，实现基本状态|0〉和|1〉的翻转;图1b的Hadamard门则把状态|0〉和|1〉分别转换为中间状态;图1c为作用在2个量子比特上的受控非门，它实现的是异或关系，当a=1时，b实现0，1的翻转， |a〉称为控制量子比特，|b〉称为目标量子比特;图1d为Toffoli门，此门有2个控制位，当|a〉和|b〉同时为|1〉时，|c〉实现0，1翻转。因此,可以让|c〉处于不同的状态，则可以发挥不同的作用。

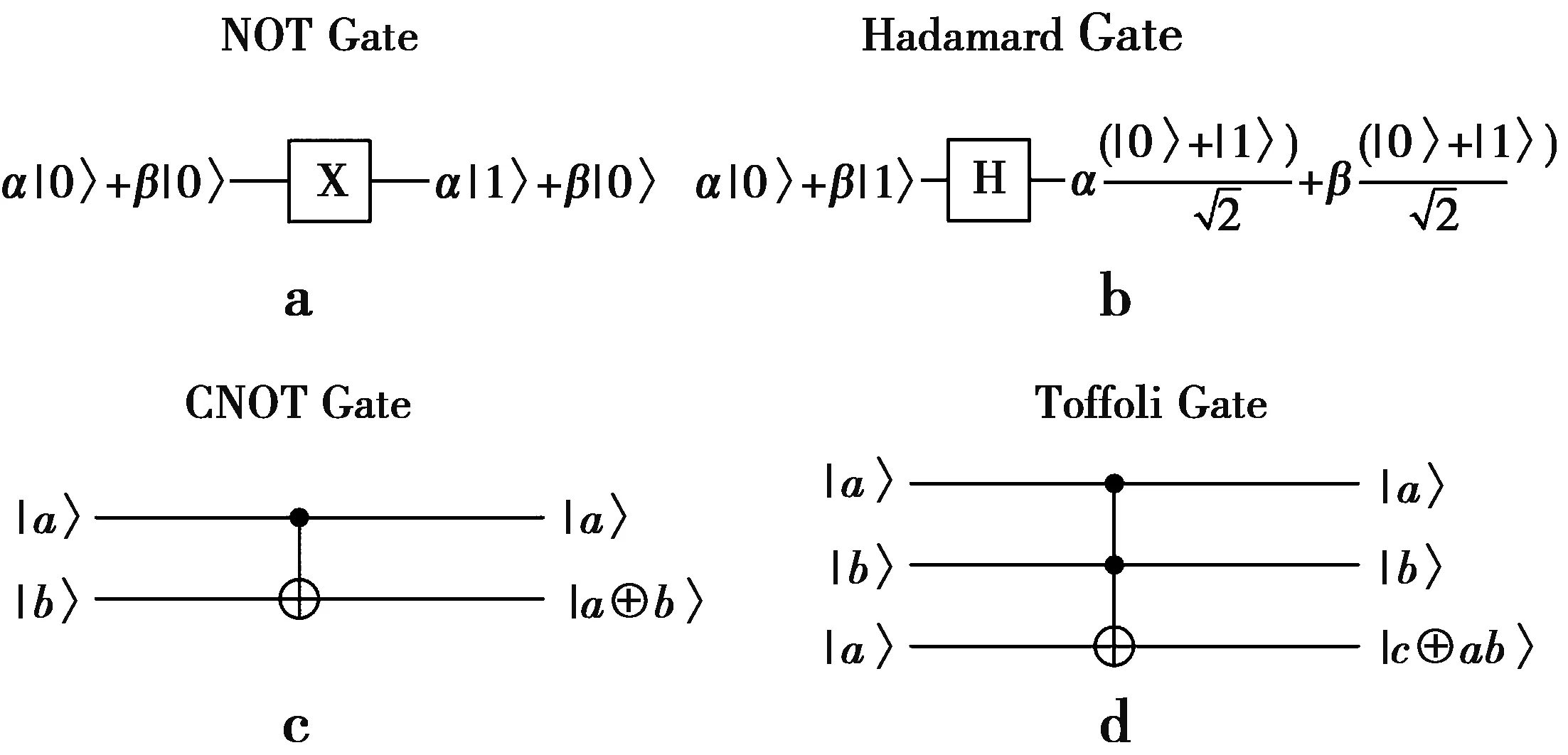
图1 通用量子门Fig.1 Universal quantum gate

1.2 计算复杂性理论

计算复杂性理论为计算机科学的一个分支[11]，与问题所需的计算资源相关。算法的复杂性是由算法解决问题时所需的时间来衡量的，算法所需的时间又由算法的执行细节以及所使用的计算机决定。对于算法的复杂性，一般指的是算法的时间复杂度。

一般地，算法的时间复杂度与输入信号的尺寸有关，即与实例有关，例如，对100个数排序比对10个数排序需要的时间更长。为了最小化时间复杂度对具体实例的依赖，一般考虑最坏情况下的时间复杂度T(n)为

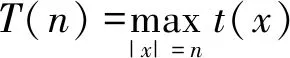
(2)

(2)式中，t(x)为输入是x时算法的运行时间。

计算算法的时间复杂度应基于一个与CPU钟频率无关的时间单元。此时间单元可为运行一个基本运算所需的时间，例如2个整数的加法运算。测量任意算法所需的时间等价于计算此算法中包含的基本运算数目。本文中以通用量子门(或叫简单量子门)为时间单元，计算所设计的量子算法时，仅需要计算实现算法的量子线路中包含的通用量子门数量。

2 量子乘法器

2.1 量子加法器

图2a展示了一位量子全加器的具体构造线路图；图2b为其简化图。用n个一位的量子全加器叠加在一起就是一个n位的量子全加器，如图2c所示，可以实现2个n位数的加和。

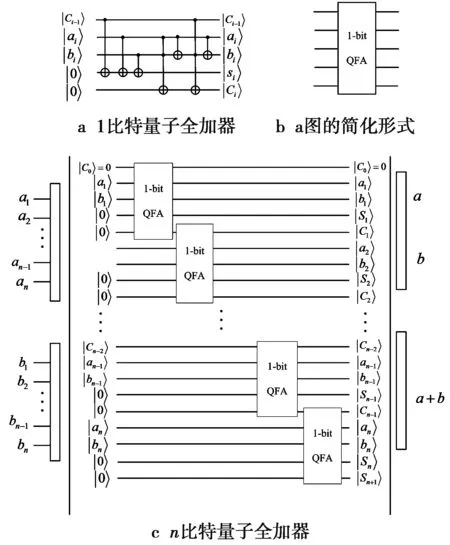
图2 量子全加器示意图Fig.2 Schematic diagram of quantum-integrator

2.2 二进制乘法的实现步骤

为了实现量子乘法运算，首先对传统乘法运算的步骤进行改进。例如，计算2个二进制数1011和1101的乘积，图3a为乘法的实现步骤。总结其规律可知，每次部分积要加的数是被乘数乘于1，或者被乘数乘于0，即每一步中，根据乘数中每一位的值，部分积加上被乘数，或者不加。根据此特点，可以设计由加法操作和右移操作协同工作的乘法步骤；图3b展示了改进后的算法步骤，首先把部分积置零，然后乘数的低位是1，所以要加上被乘数1011，然后把和右移一位；乘数高一位的数是0，就加上0000，再把和右移一位，如此循环，直到得出结果。虽然是一个简单的转换，却节省了很多计算步骤。例如，对于一个n位二进制数乘于一个m位二进制数，本来需要计算2m次的加法，改进后只需要m次加法和m-1次的右移操作。关于加法的计算可以量子加法器。接下来需要设计一个量子右移线路以解决乘法的运算。

2.3 量子右移算子

在经典的数字电路中，需要沿着每条线从头到尾来分析整个电路实现的功能，对于每条线，可以简单地对其实现扇出以及扇入操作。因为电路中的每条线代表着实际物品中的电线，和实际电线一样起着传递信息的作用，一条导线就可以把一个位置上的电位传递到任何地方，而比特的概念在电路图里没有体现得那么清楚。而在量子计算的过程中，也是按照每条线来分析其功能，不同的是，每一条线都代表一个或几个量子比特的状态转化过程，而且没有扇出和扇入操作。这是因为量子比特用更微小的物理现象表示，每条线代表的是一个相应的微观状态，例如电子的自旋方向，原子核的自旋方向等。这些状态不能简单地通过介质传递。因为量子不可克隆原理，不可能完全地对任意量子态进行复制，也就无法对任意量子态实现完全的扇出，而扇入在这里是荒谬的，因为2个量子态并不能合并。例如图4a，2个输入量子比特为|a〉和|0〉，其中，|a〉为任意的单量子比特态。可以把输入状态写作|a,0〉，表示2个量子比特耦合在一起的系统，图4a中利用了受控非门实现异或操作，经过第1个受控非门输入状态转换为|a,a⊕0〉=|a,a〉，经过第2个不同的受控非门后的输出状态为|a⊕a,a〉=|0,a〉。可以看出，这个简单的电路实现了量子比特|a〉和|0〉的交换，可以把它叫做置零线路。或者说实现了把|a〉复制到量子比特|0〉上，若把此操作应用到多位的二进制数，即可实现多位二进制数的复制操作，只不过需要n位的辅助量子比特。假设需要右移操作的二进制数是Cn-1Cn-2…C1C0，一个量子右移操作线路需要n位的量子比特来表示这个数，需要一个辅助的量子比特，辅助量子比特的初始状态一般都为|0〉，如4b所示。首先交换|C0〉和辅助量子比特|0〉，然后依次交换相邻的2个量子比特，从最终输出可以看到实现了右移操作。每次右移一共需要n次交换，共需2n个受控非门。为了使用方便，图4c为简化后的右移算符。

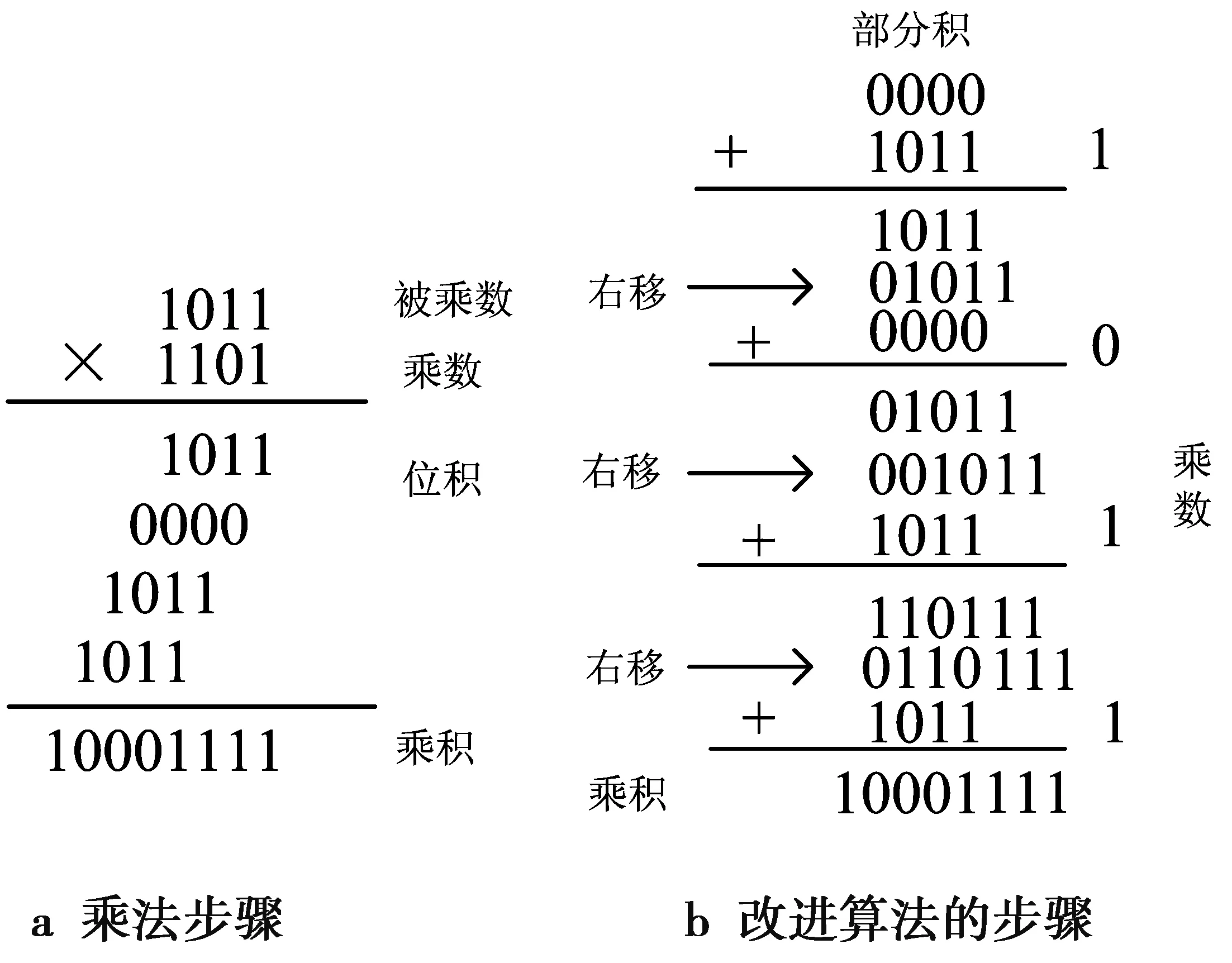
图3 乘法步骤Fig.3 Multiplication steps

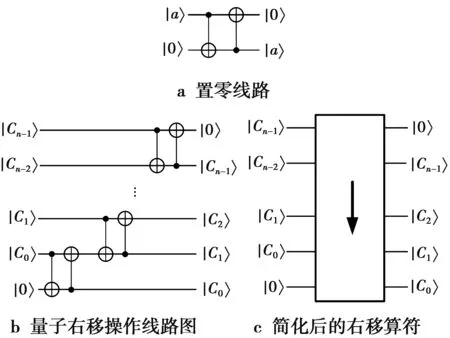
图4 量子右移操作Fig.4 Quantum right shift operation

如果需要实现很多位的右移，那么可以把整个右移算法重复使用多次，或者可以设计更简单的右移线路，图5为右移三位时的线路图。其他情况可以以此类推，同理可以设计左移操作算符。

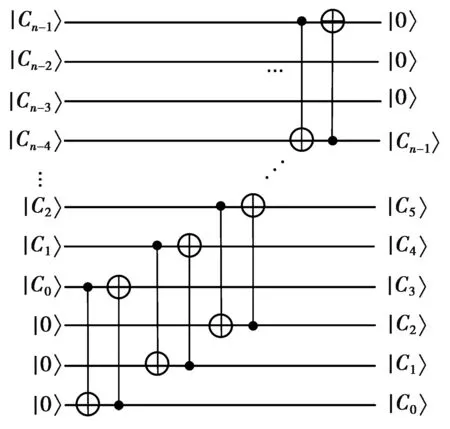
图5 右移三位算符的具体线路图Fig.5 Detailed circuit diagram of the three-right shift operator

2.4 量子乘法器设计

按照图3中的乘法步骤，使用量子加法器和量子移位算子可以设计量子乘法器。

假设要计算一个m位和一个n位的二进制数的乘积。用量子态|a〉代表n位的被乘数；|b〉代表m位的乘数。n位的部分积初始状态为零，即处于基态|0〉|0〉…|0〉，然后依次用乘数的从低位到高位的每一位来控制部分积是加上被乘数还是加零，并在每次加和之后让部分积右移一位。这样就得到了2个数的乘积。结果存储在m+n位的量子比特中。图6为量子乘法器的线路图，图6中&为量子加法器的缩写，未标注的初始为零的量子比特均为辅助量子比特。该线路图中主要有2种类型的量子门，受控加法器和右移一位操作算符，其中，受控加法器的控制量子位分别是乘数|b〉的每一位，目标位实现部分积和被乘数的加和，结果仍存储在n位部分积和一位进位量子比特|En〉中。右移操作算符作用在m+n位的量子比特上。

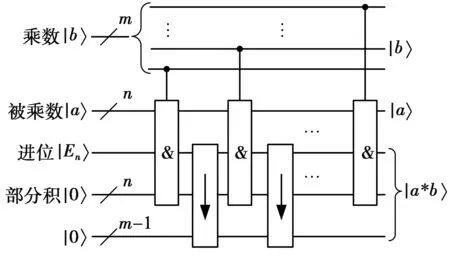
图6 量子乘法器Fig.6 Quantum multiplier

图6展示的量子乘法器原理上只能够计算2个正整数的积。然而，计算2个小数的乘积更具有普适性。只需要在图6的基础上稍作改进即可实现。对于小数，它和整数的差别是小数点位置不同，因此，可以首先忽略小数点而作为整数进行相乘，计算出乘积之后再利用图5中的量子右移算子进行移位操作即可得到正确结果。二进制数的正负使用一个比特来表示，如用0表示正数，1表示负数，而在进行数的乘法计算时，数值部分和符号部分是分开进行处理的。在乘法运算中，2个数的符号位运算规则遵循的是异或关系，图1中的受控非门即可实现这一运算。这样，经过改进后的量子乘法器便可计算任意2个有限位小数的乘积。

同样，二进制除法可以转换为减法和向左移位，和量子乘法器的过程类似，可以设计出量子除法器，这样，二进制的四则运算都可以使用量子计算的方法实现。

3 时间复杂度分析

根据算法复杂性理论，本文以通用量子门为时间单元，计算量子乘法器线路中包含的通用量子门数量，即为其时间复杂度。

对于n位二进制数乘以m位二进制数，本文所设计的量子乘法器的线路如图6所示，需要m次加法操作和m-1次右移操作。由图6可知，单比特量子全加器需要5个CNOT门和2个Toffoli门，2个n位数相加时需要n比特量子全加器，由n个单比特量子全加器组成。所以，一次加法操作需要7n个通用量子门。这样m次加法操作的时间复杂度为O(7nm)。对于一个n位二进制数，一个右移算符其时间复杂度为2n，m-1次右移操作的时间复杂度为O(2nm)。所以，整个乘法运算的时间复杂度为O(nm)。如果计算的二进制数都是n位，则其时间复杂度为O(n2)。

文献[8]设计了基于二叉树的量子乘法器，其时间复杂度为O(n3)。文献[9]利用乘数累加单元、量子全加器和量子“与”操作设计了目前最高效的量子乘法器，其时间复杂度为O(n2)。本文所设计的量子乘法器时间复杂度也为O(n2)，并且本文算法的结构更简单，仅需要加法操作和右移操作。可见，本文的量子乘法器设计是三者中最优的方案。

4 结束语

本文设计了一种量子乘法器，通过量子全加器实现了n位二进制数的加和，并且利用2个控制非门设计了置零电路，并使用置零电路设计量子右移算子。改进了二进制乘法，按照改进后的步骤设计了量子乘法器。此设计充分考虑了每个二进制数存储在一个量子态中，对每个二进制数进行整体操作时更节省资源的特点，提供了一个合理的二进制数乘法步骤。时间复杂度分析表明，本文所设计的量子乘法器，与文献[8]中设计的量子乘法器具有相同的时间复杂度，但具有更简单的实现方法。