张量稀疏性度量综述

谢 琦，张 勇，孟德宇

(1.西安交通大学 数学与统计学院，西安 710049；2.西安交通大学 第一附属医院，西安 710049)

0 引 言

从通常意义上理解，先验是一个与经验相对的概念。它先于经验，却对经验的形成有着很大的影响，甚至有时它是经验形成不可或缺的部分。在机器学习问题中，如果观测数据中能提供的经验信息不是非常充分，或是观测数据中蕴含的经验信息难以利用时，先验知识的指导作用将变得尤为关键。从数学上看，先验知识的作用可以通过模型中的正则函数体现。当损失函数对应的模型是欠定问题或近似欠定问题时，它可以引导模型筛选得到合理的解。举如下的数据恢复模型为例

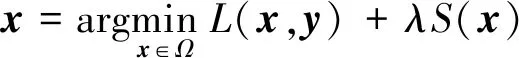
(1)

稀疏性是一种很多现实数据都共有的一般化属性，因此，它作为一种常见的数据先验在大量应用问题中得到了广泛的关注。

简单来说，稀疏性是指现实数据可被少数基元素进行充分表达的特性。很多类型的应用数据本身就具有稀疏性特点，而也有不少数据通过某种变换，也具备较为显著的稀疏性特征。依旧举图像去噪问题为例，当用TV范数刻画“自然图像是比较平滑的”这一属性时，其实可以等价理解为把这一属性近似地用“自然图像数据在差商变换后将具有较强稀疏性”这一易于表达的属性进替换。这意味着经过了差商变换的自然图像，具备了稀疏性的特点。

由于现实数据广泛具有的稀疏性特征，如何使用量化方式有效刻画数据稀疏性度量，即如何构造有效刻画数据稀疏性的正则函数形式，是机器学习、数据挖掘、模式识别等诸多领域关注的问题。

对于具有向量(1阶数组)与矩阵(2阶数组)形式的数据，已存在较为成熟的稀疏性表达度量。本文将向量意义下的稀疏性称为1阶稀疏性，对应的稀疏性度量称为1阶稀疏性度量；在矩阵意义下，低秩性可以理解为表达矩阵所需的最少基底的数量，这正满足我们对稀疏性的定义。出于一致性的考虑，本文将矩阵的低秩性称为2阶稀疏性，对应的稀疏性度量称为2阶稀疏性度量。目前，1阶稀疏性度量与2阶稀疏性度量均存在受到广泛认可的数学表达形式，我们一般用向量形式数据中的非零元素个数(即l0范数)作为1阶稀疏性度量，用矩阵形式数据的数据矩阵秩作为2阶稀疏性度量。这2种稀疏性度量及其松弛形式(如，l1范数与核范数)都展示出对稀疏性良好的刻画能力，延伸出一系列基于稀疏或低秩的数学模型[1-8]并已得到广泛的应用。

然而，对于张量(高阶数组)数据的合理稀疏性度量的构造，尽管已有一些研究，但仍然尚未形成统一的解决方案。本文将对张量稀疏性研究的现状进行综合介绍，回顾目前在此方向的研究进展以及所取得的典型应用，并着重介绍本研究小组所构造的一种新型张量稀疏性度量。相比传统度量，所提出的张量稀疏性度量不仅充分编码了对于张量的2种经典分解方式(Tucker分解与 CANDECOMP/PARAFAC (CP) 分解)的稀疏性内涵，而且具有与传统的向量/矩阵稀疏性度量的统一性，并且蕴含显著的物理含义(张量表达的1秩Kronecker基个数)，几种张量分解展示如图1。其中，αi(i=1,…,k)代表基向量，σi(i=1,…,r)代表矩阵的奇异值向量。此外，也将介绍此张量稀疏性度量在多光谱图像去噪、填充等问题中获得的state-of-the-art应用表现，从而说明其合理性与有效性。

1 高阶稀疏性度量的研究现状

随着数据获取技术的飞速发展，用以描述数据的特征结构越来越丰富与复杂，更多问题中的数据往往呈现高阶数组，即张量的表达格式。此时，机器学习更适宜在张量上直接操作，而非将其简化为向量或矩阵的格式，从而避免有用结构信息的损失。因此，一个自然的问题就是如何将1阶与2阶稀疏度性度量向高阶张量做有效推广。相比1阶与2阶情形，高阶张量具有更加复杂的代数性态与物理特性，对其构造有效稀疏性度量也具有更大的难度，对该问题目前仍未形成学界公认的统一解决方案。

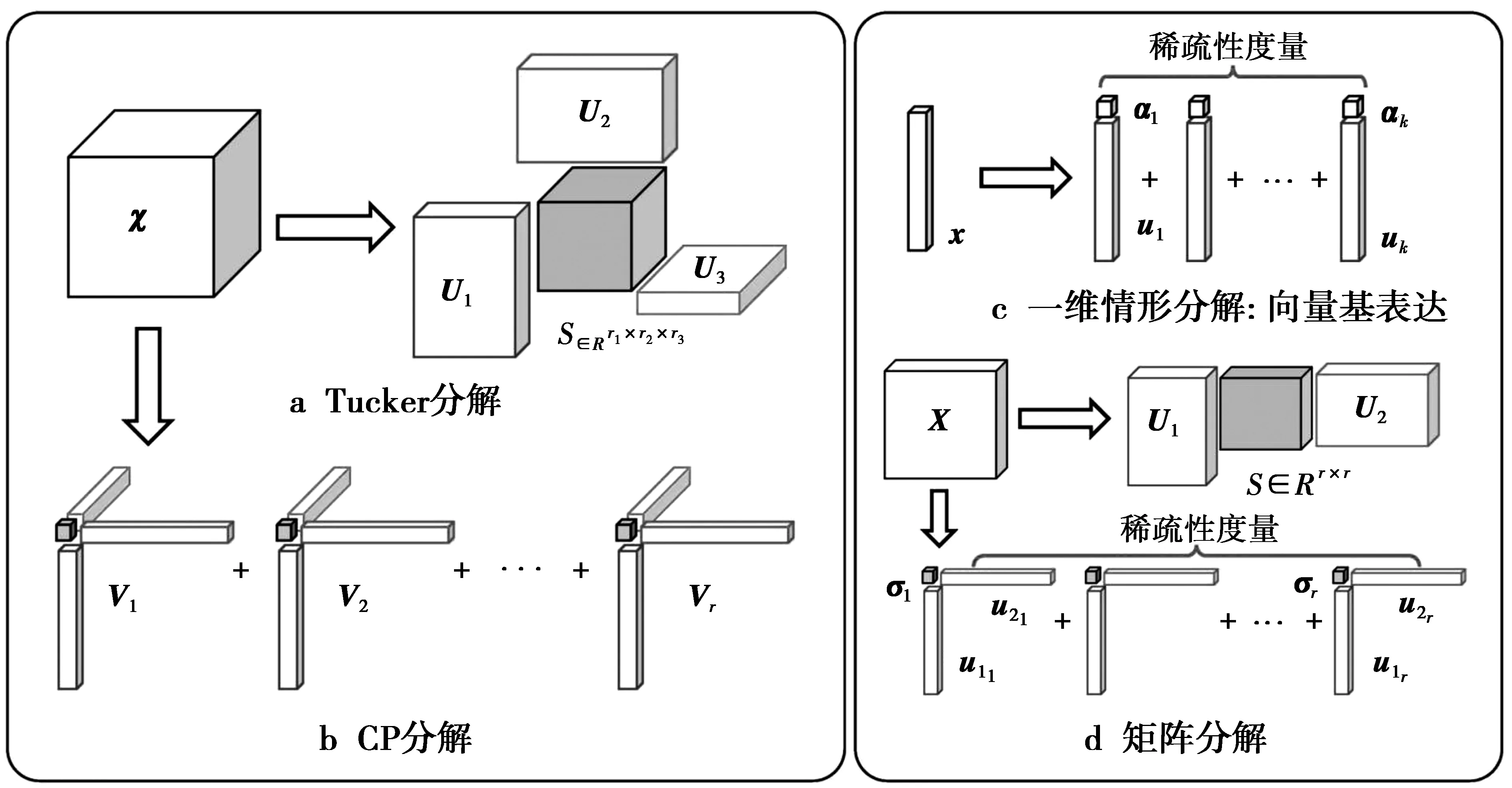
图1 几种张量分解的展示Fig.1 Demonstrations of several tensor decomposition formats

CP秩是一种典型的高阶稀疏度量[9]，其定义为组成目标张量的最少秩1张量的个数。CP秩作为高阶稀疏性度量的优点是其与传统的1阶与2阶稀疏性度量一致，并且定义十分简单直观。然而，CP秩的计算是一个NP难的问题，且很难构造方便计算的松弛形式，其计算的困难性导致其很难有效应用于真实的稀疏建模问题中。

另一种典型的高阶稀疏性度量是Tucker秩[10]，其定义为一个由张量各个方向展开矩阵的秩组成的数组(其长度为张量的维度数目)。因为Tucker秩是基于矩阵秩定义的，所以其计算较为方便，往往可直接基于矩阵相关的计算技术直接移植改造。但Tucker秩是一个数组而非实数，所以并不合适直接用来作为模型的优化目标。可采用如下简单直观的方法将其量化[11]

(2)

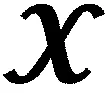
(3)

因此，现有的高阶张量稀疏性度量仍有一定的缺陷，存在提高的空间。针对这一问题，对高阶张量稀疏性进行进一步探讨，并尝试给出一种新的高阶稀疏性度量。

2 一种新的高阶稀疏性度量

在给出新的稀疏性度量之前，首先通过CP分解与Tucker分解对高阶稀疏性的本质进行简单的探讨。

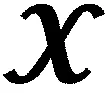
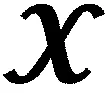
(4)

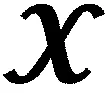
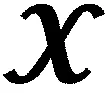
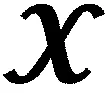
(5)

(5)式中，S∈RR1×R2…×RN，ri≤Ri≤Ii。当对基矩阵Ui中的列合理排序时，S中的非零元将只分布在左上角r1×r2…×rN大小的方块区域内。此时，可以看到，Tucker秩(r1,r2,…,rN)即核张量中方块非零区域的各边大小。然而，实际的3阶数据的核张量中，非零元元素沿各层呈现较为复杂的变化形态，Tucker秩并不能有效刻画这样的非零分布差异性，而仅提供了能够包含所有非零分布的一个张量块的大小，提供了一个较为粗糙的核张量非零元个数上界，图2展示了一个简单的例子。

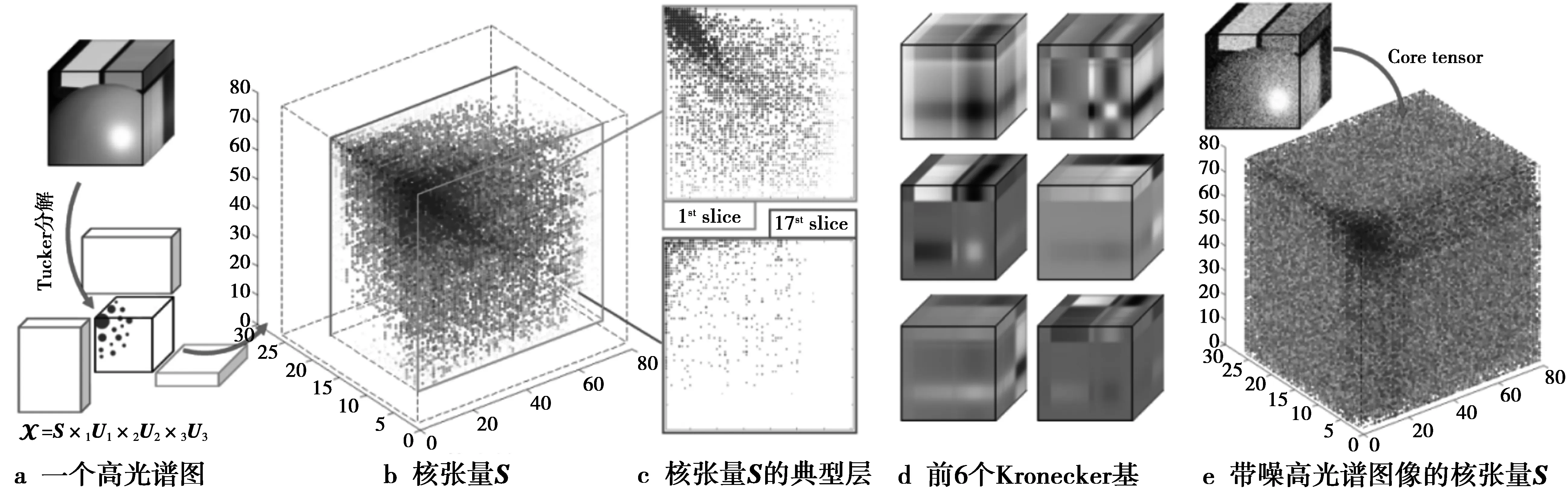
图2 干净与带噪的高光谱图的核张量示例Fig.2 Illustration of the core tensors of the clean and noisy multispectral images

从上面的分析中可以观察到，无论CP秩还是Tucker秩对张量的稀疏性的刻画都不全面，而他们刻画的内容一定程度上是互补的。事实上，Tucker分解也可以写成秩1矩阵加和的形式

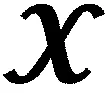
(6)

(6)式中：ui1,…iN为所有Uj的第ij列的积(j=1,…,N)得到的秩1张量。S中非零元素的个数即代表张量需要的Kroneker基的个数(与CP分解中的Kroneker基的不同在于这里的Kroneker基是由各基矩阵Uj的列外积而来)，其提供了CP秩的一个上界，由此，可以看出Tucker分解的核张量提供了一个CP秩的约束。

基于以上认识，我们认为核张量中与高阶稀疏度相关的信息主要可以归纳如下。

1)细描述：核张量的非零元素的数量(细致刻画核张量中非零元分布)

2)粗约束：核张量中方块非零区域的大小(提供核张量非零元个数的上界)

其中，2)也是Tucker秩以及秩和(2)式稀疏性度量的刻画内容。

基于上述对张量稀疏性的认识，提出了如下的高阶稀疏性度量[19]

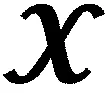
(7)

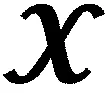
相比传统张量稀疏性，该度量具有如下一些独特的优点。

1)所提稀疏性度量具有明确物理意义。其第1项度量了表达张量所需的Kroneker基数量，第2项刻画了表达张量所需Kroneker基数量的一个约束上界。两者的意义是统一的，第1项是对Kroneker基数量的细致刻画，第2项是对该数量的一个正则约束。

2)所提稀疏性度量与传统1阶与2阶稀疏性度量内涵具有一致性。传统的1阶向量稀疏性可理解为其在特定字典下本质表达原数据的向量基，即1阶Kroneker基个数；2阶矩阵稀疏性即为表达原数据所需秩1矩阵，即2阶Kroneker基个数。因此，其物理意义完全统一。而从表达形式上来看，对于1阶稀疏性度量‖x‖0，所提稀疏度量为S(x)=t‖x‖0+(1-t)‖x‖0，显然，其关于‖x‖0是单调的；对于传统2阶稀疏性度量rank(X)，所提稀疏度量为S(X)=t·rank(X)+(1-t)·rank(X)2，显然，它关于rank(X)也是单调的。因此，从对稀疏性的量化刻画上看，与传统稀疏性度量具有一致性。

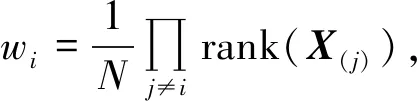
(8)

这说明，只要合理选取wi，传统的加权秩和形式的正则作用与所提模型的第2项将十分相似。反过来，(8)式也提供了一种wi的选取方式，不难推出这种选取方式在直观是非常合理的：低秩性强的方向要对应更大的权，低秩性弱的方向要对应更小的权。

3 实验结果

本节将简单展示所提稀疏性度量应用到多光谱图像去噪的实验结果。

这个实验中，将所提的稀疏性度量应用到多光谱图恢复过程中，相似全光谱图块的相似组组成的3阶张量恢复模型中(构建的方法记为ITS-denoising)，具体的方法可以参见文献[20]。

对比方法包括K-SVD[21]， BM3D[22]作为逐帧图像处理方法的代表，3DK-SVD[23]， ANLM3D[24], BM4D[25]作为3D小块上处理方法的代表；LRTA[26]， PARAFAC[27]， TDL[28]， t-SVD[18]，LRTV[29]作为其于张量恢复类的方法的代表。使用的评价指标包括：峰值信噪(peak signal-to-noise ratio, PSNR)，结构相似性(structure similarity， SSIM)，特征相似性(feature similarity， FSIM)和ERGAS(erreur relative globale adimensionnelle de synthèse)。其中，前3个指标越高代表去噪效果越好，而最后一个指标越高代表去噪效果越好。

在Columbia 多光谱图数据[25]上进行仿真实验，这个数据中有32个多光谱图，每个多光谱图的大小为512×512×31。分别测试了数据人工加入标准差在0.1～0.3之间的几种高斯噪声后进行去噪的实验效果。实验结果如图4与表1。图4a为多光谱图chart and staffed toy的2帧；图4b为方差为0.2的带噪图片展示；图4c—图4m为11种方法的处理结果对比，其中，2个方框区域是对应的2个小框区域的放大并提高相同亮度的结果。容易看出，不论在数值比较上还是视觉效果上，所提稀疏性度量都能较大地提升多光谱图像去噪的精度。表1最后一行数字为最佳结果。

图4 10种对比方法及所提的ITS-denoising方法在chart and staffed toy的2帧上的结果展示Fig.4 Result of the 10 competing methods and the proposed ITS-denoising method at two bands (400 nm and 700 nm) of chart and staffed toy

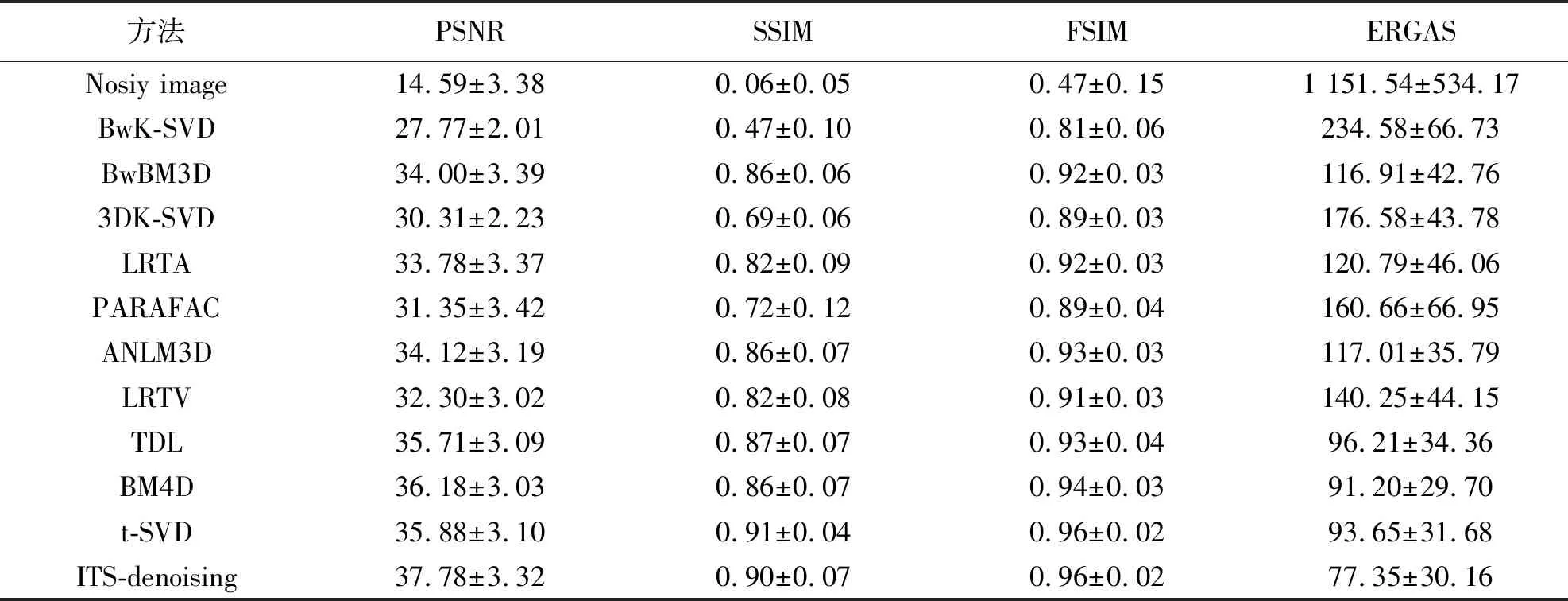
方法PSNRSSIMFSIMERGASNosiy image14.59±3.380.06±0.050.47±0.151 151.54±534.17BwK-SVD27.77±2.010.47±0.100.81±0.06234.58±66.73BwBM3D34.00±3.390.86±0.060.92±0.03116.91±42.763DK-SVD30.31±2.230.69±0.060.89±0.03176.58±43.78LRTA33.78±3.370.82±0.090.92±0.03120.79±46.06PARAFAC31.35±3.420.72±0.120.89±0.04160.66±66.95ANLM3D34.12±3.190.86±0.070.93±0.03117.01±35.79LRTV32.30±3.020.82±0.080.91±0.03140.25±44.15TDL35.71±3.090.87±0.070.93±0.0496.21±34.36BM4D36.18±3.030.86±0.070.94±0.0391.20±29.70t-SVD35.88±3.100.91±0.040.96±0.0293.65±31.68ITS-denoising37.78±3.320.90±0.070.96±0.0277.35±30.16

同时也在Urban多光谱图数据上进行实际数据的去噪实验，结果如图5，图 5a为多光谱图Urban的一帧; 图5b—图5l为11种方法的结果对比，可以看出，所提稀度量能较为明显地在保持图像细节的前提下去除噪声。

4 总 结

本文基于前人的工作，对高阶张量稀疏性度量进行了探讨，认为其本质与张量秩1的Kroneker基个数紧密相关，并借由张量Tucker分解与CP分解中对Kroneker基相应的内涵理解构造了新型的张量稀疏性度量。相比已有度量，其不仅具有显著的物理含义，且与传统的1阶与2阶稀疏性度量具有内在一致性。特别地，其可以提供传统张量稀疏性度量的加权格式理解。在多光谱数据的去噪、填充与视频数据的背景提取问题中，所提张量稀疏性度量均体现了显著的应用有效性。在未来的工作中，将研究如何使用更简单的形式对所提的2个性质进行刻画，并进对所提的稀疏性度量的理论性质进行必要的研究。

图5 10种对比方法及所提的ITS-denoising方法在 Urban 数据的一帧上的结果展示Fig.5 Result of the 10 competing methods and the proposed ITS-denoising method at two bands of Urban data set