无线传感器网络基于改进遗传算法的节点调度
陈立万,杨 震,李洪兵,陈 强
(1.重庆三峡学院 教师教育学院,重庆 404100;2.重庆三峡学院 电子与信息工程学院,重庆 404100;3.重庆三峡学院 计算机科学与工程学院,重庆 404100)
0 引 言
无线传感器网络(wireless sensor networks, WSNs)由传感器节点构成,能够感知、采集和传输信息。因为节点自身能量有限,如何实现节点能耗均衡、延长网络生命周期是无线传感器网络的一个研究重点[1]。节点调度可使一部分节点处于休眠状态,减少网络能耗,提高网络通信性能,又能保证整个网络系统正常工作。
节点调度问题在交通运输、物流选址、配送等领域内应用广泛[2]。长期以来人们一直在寻求快速、高效的求解算法,即在给定优化性能指标和满足给定约束情况下[3],通过物流的方式,将合适的材料交付到理想的位置。然而随着节点数的增加,路线数将会呈指数级增长,目前多数算法仍不能在较短时间内给出最优解[4-6]。虽然国内外一些专家用遗传算法解决节点调度问题[7],并且取得了一定的成果,但仍然存在一些缺陷[8],如选择算子的适应度比例选择[9],在执行过程中容易停滞,当规模较大时易陷入局部最优。Ammar Al-Dallal[10]证明了所提出的两段染色体交叉法可以有效提高遗传算法的搜索能力,然而其算法的收敛速度很慢且路径也不是最优路径;Alkhayri等[11]提出一种新的选择算子,称为聚类选择法,虽然迭代次数变少,但其收敛性变差;Wang等[12]提出了一种多子代遗传算法,该算法在选择过程中提高了优秀个体的概率,同时也使得种群更具竞争力,然而其搜索的路径并非最短;J.B.Escario[13]运用蚁群算法通过状态空间探索方法执行搜索,但随着路径长度的增加,其寻优能力变差;Mavrovouniotis[14]提出一种模因子蚁群算法,将局部搜索算子集成到蚁群中,该算法提高了寻址效率,但所求的路径并非最优路径;Su等[15]提出一种改进的粒子群算法,利用贪婪算法对粒子群进行初始化,将遗传算法中的交叉和变异算子引入到新算法中,提高了算法的收敛性,但其算法的复杂度和运行时间不够理想。Ahmed[16]提出一种基于粒子群算法的启发式算法,改进后的算法减少了寻优时间,但是所求解的路径不是最优路径。
蚁群算法(ant colony algorithm, ACO)是基于对自然界真实蚁群的集体觅食行为的研究,模拟真实的蚁群协作过程。算法由若干个蚂蚁共同构造解路径,通过在解路径上遗留并交换信息素提高解的质量,进而达到优化的目的。蚁群算法成功应用于节点调度等一系列组合优化问题中,并取得了较好的结果。但由于该算法是典型的概率算法,在解决节点调度问题中,参数设定会导致求解速度很慢且所得解的质量特别差,且计算量大,求解所需时间较长。粒子群优化(particle swarm optimization, PSO)算法是利用群体中个体对信息的共享,在问题求解空间中产生从无序到有序的演化过程,从而获得问题的最优解。然而粒子群优化算法应用解决节点调度问题时容易产生早熟收敛、局部寻优能力较差,粒子在搜索空间中多样性的丢失等缺点。
本文提出一种改进遗传算法,该方法基于适应度比例的选择,使用优化的轮盘赌方法来选择当前组中具有较高适应度的个体,然后交叉变异并筛选具有最高适应度的下一代,确定出最优路线,进而快速精确地求出节点调度问题的最优解。通过与蚁群算法、粒子群算法以及经典的遗传算法进行比较。仿真实验表明,该算法在相同条件下具有更有效的寻优能力。
1 调度问题描述
节点调度对于无线传感网络节点寻优求解有重要的指导作用。采用改进的遗传算法进行选择、交叉、变异等操作,可以快速实现能量有效性问题的求解,且得到的解收敛性强,不易陷入局部最优。
节点调度问题可描述为,n个节点及其节点间的距离给定后,找寻一条遍历每个节点且所有节点只能被访问一次的路径,获得最短总路径。其数学描述如下所示。
赋权图设为G=(V,E),顶点集V={1,2,…,n},边集E,顶点间距Cij,且Cij>0(i,j∈V),并设
(1)
综上,节点调度问题的数学模型可表示为
(2)
(2)式中:xij=1表示节点运动走最优路径;xij=0表示节点运动时走其他路径;K是V的非空真子集;|K|是集合K中包含图G的全部顶点个数。
2 改进的GA算法
本文通过对选择算子的优化,以及利用优化的轮盘赌方法对经典的GA算法进行改进,选择当前群体中高适应度个体交叉和变异,筛选出适应度最高的下一代。
2.1 选择算子
保留群体中具有较高适应度的个体,删除较低适应度的个体称为选择。目的是遗传高适应度的个体给下一代,并从群体中移除劣质个体。在选择过程中,最常用的选择算子有随机遍历抽样、局部选择、适应度比例。本文中,改进后的轮盘赌选择法用于选择高适应度的个体,剔除低适应度的个体。
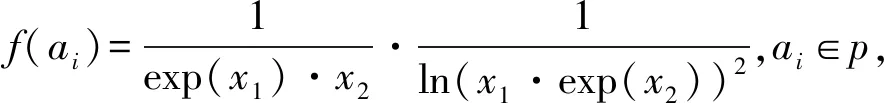
(3)
(3)式确定了后代种群中个体的概率分布。其中,在父代种群中个体生存量为p(aj)=np,j=1,2,…,n。本文中,全局选择模式在保留高适应度个体的同时剔除低适应度的个体,直到适应度低的个体全部剔除。当个体的规模与后代的比例相等时,计算出的期望值p(ai)不是整数,如果采取四舍五入的方法,种群的规模会在后代种群求和之后发生变化,采用轮盘选择的方法可以解决该问题。
2)优化轮盘选择。优化的轮盘赌选择是从染色体群体中选择个体的方法,被选中的几率与其适应度成比例,染色体适应度越高,被选中的概率越大。假设群体全体的个体适应度用一张饼图代表,则该饼图与赌博的转盘类似。种群中每条染色体代表饼图中的区域,区域的大小与染色体的适应度大小成正比,适应度越高,所占面积越大。为了选取一个染色体,需要旋转轮盘,然后把小球抛入其中,让小球在轮盘中不停跳动,直到轮盘停止转动,小球最终停在哪一区域则选中与之对应的染色体,轮盘模型如图1所示。
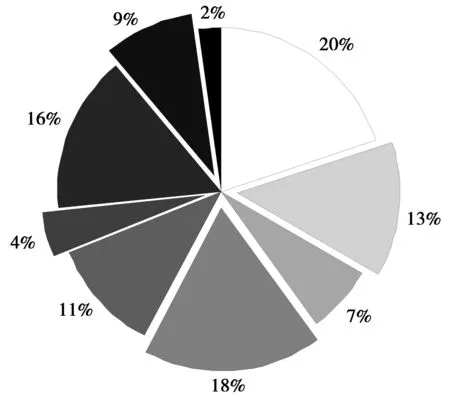
图1 轮盘模型Fig.1 Roulette model
若把圆形的轮盘抽象成一把游标卡尺,尺子可分为多段,箭头(随机产生的阈值)在尺子的长度范围内随机移动。对于基因组的适应度区域,适应度越大,该组基因占有的区域越大。
用全部个体的选择概率来计算累积概率。第k个个体的累积概率为
(4)
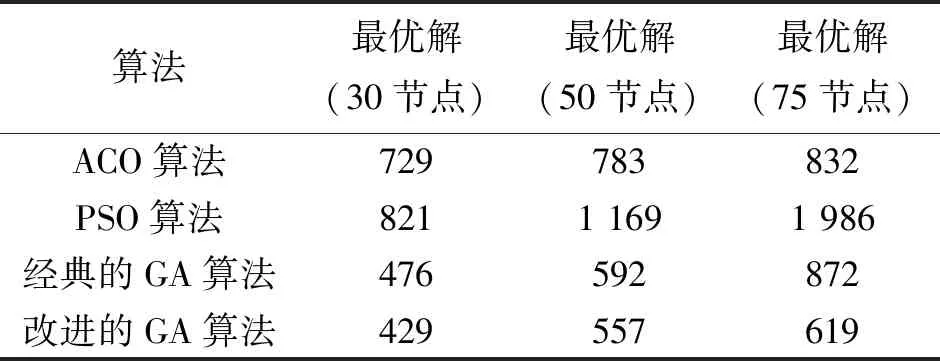
然后生成随机数e(e∈[0,1]) 与px(ak)进行比较来确定选择个体。如果ak-1 (5) 然后,产生(n-m)完整的子代个体。存活的种群p(aj)的所有个体按降序排列。选择顶端的(n-m)个体构成一个完整的子代。例如,第k个个体ak是在(n-m)最上面的个体,在后代中,第k个个体的实际选择数量是(x(ak)+1)。 为提高遗传算法的搜索能力,两父代个体的部分结构被替换和重组以产生新个体。群体中任意的2个个体随机交换某些基因,并根据设定的交叉率产生新基因组合。交叉时采用部分映射杂交,进行基因重组,选择出具有高适应度的个体,更新基因库。 首先确定要进行交叉的父代,然后把父代两两分组,每个组重复下面过程(假定的城市数为10),产生[1,10]的2个随机数r1与r2,明确其2个位置后再对中间的数据进行交叉操作,如r1=5,r2=8。 交叉后为 经过交叉后,重复的城市编号异号数字保留,带*号的采用部分映射法,即用中间段对应关系进行映射。其结果为 首先,判断种群中的所有个体是否符合预先设定的变异概率,然后选择需要变异的个体在其变异位置进行变异。随机选取2个点,对换其位置并进行变异操作。生成[1,10]的2个随机数r1与r2,明确其位置,然后对换位置,如r1=5,r2=8。 {x9x4x1|x6|x3x7|x8|x10x5x2}, 变异后为 {x9x4x1|x8|x3x7|x6|x10x5x2}。 本文解决节点调度问题采用了自适应的交叉型和适应变异算子机制,采用了每一代的交叉和突变后保留最优值的策略。通过机制优化,得到不同选择模式对遗传算法的影响结果。图2显示了改进GA的节点调度算法流程图。 图2 改进GA算法流程图Fig.2 Flowchart of improved GA algorithm 算法伪代码设计如下。 输入:节点调度实例,种群规模popsize; 输出:最优解。 1.编码和种群初始化 2.计算节点的顶点间距Cij 3.计算个体适应度f(ai) //选择操作 4.优化的轮盘赌选择策略 5.计算选择概率Ps(aj), 累积概率Px 6.对每个个体,如果r>P(ai-1) andr 7.选择适应度最高的个体 //交叉操作 8.计算交叉概率Pc 9.选择最好的个体 10.交叉前用最好的个体代替最差的个体 //变异操作 11.计算变异概率Pm 12.将个体基因片段从j到k进行反转 13.判断是否获得最优解 14.获得最优解时迭代停止,否则回到步骤3重新计算。 本文选取100×100的无线传感区域,采用MATLAB2014a仿真软件进行仿真。通过ACO,PSO,经典的GA算法与改进的GA算法对最优路径、收敛性以及运行时间3个指标进行对比仿真实验,以证明改进的GA算法的优越性,具体实验结果如下。 1)最优路径仿真。4种算法的最大迭代次数均设置为500次;算法中初始种群的数量设置为100;传感器节点的坐标参数相同,依次设置为30个和75个;每个个体具有相同数量的基因,每组实验重复100次并进行数据分析。模拟4种算法以获得30个节点的最佳路线如图3,75个节点的最佳路线如图4。依据传感器节点之间的距离连线,可以看出4种不同的算法其节点间的路径不同。当里面任一节点失效时,相邻节点填补其位置的时候所走的距离不同,其能量和时间的消耗也不一样。 最优路线数据统计如表1。 表1 算法的数据(每种运行100次)Tab.1 Data for the algorithm (100 times per run) 图3 30个节点路径图Fig.3 30-node path map 图4 75个节点路径图Fig.4 75-node path map 表1显示了本文实验结果在最优解的准确性方面的统计,其中,最优解表示最短路径。实验结果表明,经过500次迭代的情况下,节点为30个时,4种算法中ACO算法和PSO算法路线分别是729和821,比另外2种路线长。经改进后的GA路径为429,比经典的GA算法短,距离减少了47,改进的GA算法路径明显比蚁群算法与粒子群算法结果好。节点为75个时,4种算法中ACO算法和PSO算法路线分别是783和1 169,比另外2种路线长。经改进后的GA路径为619,比经典的GA算法短,距离减少了35,改进的GA算法路径明显比蚁群算法与粒子群算法结果好,比经典的GA算法的最优路径也有较大改进。节点为75个时,4种算法中,ACO算法和PSO算法路线分别是832和1 986,比另外2种路线长。经改进后的GA路径为619,比经典的GA算法短,距离减少了253,改进的GA算法路径最短。 2)收敛速度仿真。种群的初始数量设置为100;最大迭代次数设置为500次;传感器节点的坐标参数设置为30个和75个;每个个体具有相同数量的基因,并且每组实验重复100次。通过仿真实验,分析500次迭代后4种算法的适应度函数曲线变化,如图5和图6。 在算法迭代0—20次时,对比图5和图6中的4种算法,ACO算法和PSO算法随着迭代次数的增加函数收敛速度非常快,这样将会导致算法陷入局部早熟。在种群迭代约20~250次的时候,适应度函数曲线逐渐达到稳定状态,ACO算法的适应度值分别为729和864,PSO算法的适应度值为873和1952,GA算法的适应度值为491和885,而改进的GA算法计算出的适应度值为435和643。种群迭代500次的时候,4种算法的适应度函数曲线不再变化。此时,ACO算法计算出的适应度值为729和832,PSO算法的适应度值为821和1986,GA算法的适应度值为476和872,改进的GA算法的适应度则为429和619。可以看出,改进的GA算法收敛性能比另外3种算法更高,表示全局寻优能力更强,结果最理想。 图5 30个节点适应度函数变化曲线Fig.5 Variation curve of the fitness function of 30 nodes 图6 75个节点适应度函数变化曲线Fig.6 Variation curve of the fitness function of 75 nodes 3)运行时间仿真。500次迭代后,4种算法运行所需要的时间如图7。 图7 算法运行时间Fig.7 Algorithm run time 由图7可知,节点数为30时,蚁群算法所用时间为1 326,粒子群算法所用时间为312,遗传算法所用时间为487,改进的遗传算法所用时间为389;节点数为50时,蚁群算法所用时间为1 874,粒子群算法所用时间为527,遗传算法所用时间为786,改进的遗传算法所用时间为544;节点数为75时,蚁群算法所用时间为2 685,粒子群算法所用时间为832,遗传算法所用时间为1 013,改进的遗传算法所用时间为858。显然,改进的GA算法运行时间比粒子群算法运行时间略长,但比蚁群算法和经典遗传算法运行时间明显缩短,优势仍然明显。 一般迭代方法容易陷入局部极小的陷阱,出现“死循环”现象,使迭代无法进行。优化的遗传算法克服了该缺点。遗传算法3个算子的实现有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,目前这些参数的选择大部分是依靠经验。本文采取适应度选择的方法,优化轮盘赌选择模型,使选择模型更符合“适者生存”的原则,其优化方法保留了优秀的个体并防止了最佳解决方案的丢失。经过仿真比较,该改进的GA算法,其路径长度、收敛性与运行时间等指标改善明显。2.2 交叉算子
2.3 变异算子
3 改进的GA求解
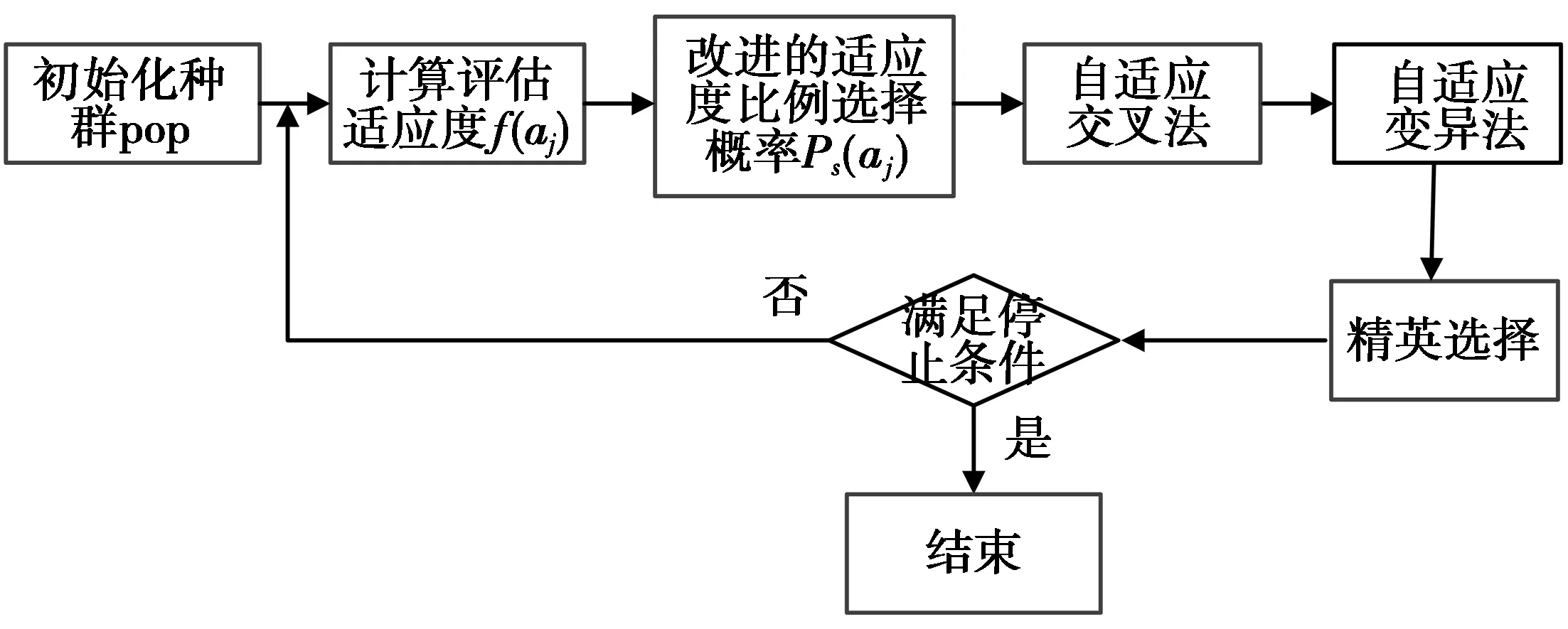
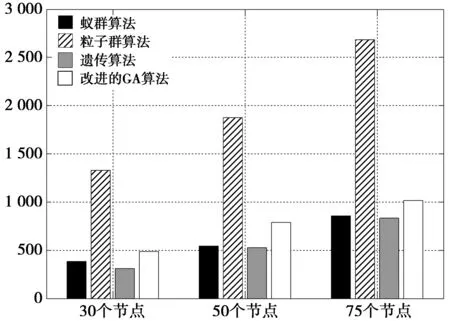
4 仿真分析
5 结 论

