基于用户簇分布模型的三维异构蜂窝网络覆盖概率分析

李中捷，刘倩倩，陈燚雷

(中南民族大学 智能无线通信湖北省重点实验室，武汉 430074)

0 引 言

由于移动用户数量的暴增，导致移动数据流量呈指数增长，因此传统的蜂窝网络逐渐演变成低功率小基站与宏基站共存的异构蜂窝网络。均匀部署的宏基站提供了大部分的覆盖，低功率小基站补充蜂窝网络(主要是热点区域)的容量或者是填补覆盖盲区，这使得小基站和用户的空间位置存在相关性。因此，在分析异构蜂窝网络性能时，应该考虑蜂窝用户以小基站为中心的簇分布情况，从而体现小基站和用户的空间位置关系。此外，蜂窝网络通常在二维空间上建模与分析。这种模型适用于郊区区域，并不适用于密集的都市环境[1]。尤其是我国大中城市的商务办公区、高层住宅小区和大型购物中心等地居多，因此研究三维空间异构蜂窝网络中，用户聚集在小基站附近的模型非常必要。

文献[2]在三维空间中利用独立均匀的泊松点过程对宏基站、低功率小基站和蜂窝用户进行建模，推导得到了下行链路的覆盖概率，分析了影响覆盖概率性能的诸多参数配置。文献[3]基于alpha stable过程分析了具有同信道干扰的多小区蜂窝网络的下行链路平均容量。文献[4]首先基于马尔科夫链提出一种新无线信道接入模型，并基于该模型提出新的空间谱和能量效率模型，分析了中断概率、能量效率等性能。文献[5]构建了基于基站密度和业务负载的网络能效模型，根据网络业务流量的到达率对基站密度进行联合优化，提高了能量效率。文献[6]基于二维的泊松点过程，联合优化中继站位置与服务范围对增大能量效率进行了分析。文献[7]基于三维空间的泊松点过程模型建模实际城市环境下密集毫米波蜂窝网络中基站的分布，推导了平均覆盖概率的理论表达式。文献[8]在二维空间内考虑小基站部署在目标用户附近，基于条件稀释的方法，提出一种用户与基站空间位置相关的通用模型，并分析了覆盖概率的性能。文献[9-10]在二维空间内采用泊松点过程对基站的分布进行建模，采用泊松簇过程对用户的分布进行建模，基于最大平均接收功率的接入方式分析了覆盖概率。文献[11-12]在二维空间内采用泊松簇过程对基站与用户的分布进行建模，基于最大信号干扰比接入方式分析了覆盖概率。

本文针对三维空间下的异构蜂窝网络，提出基于用户的簇分布模型。首先采用泊松点过程对各层基站的分布进行建模，以小基站为父节点，分别采用Matern簇过程和Thomas簇过程对聚集在小基站附近的用户进行建模。然后根据最大信号干扰比的小区接入准则，推导出覆盖概率的理论表达式，并且通过蒙特卡罗仿真验证理论结果。最后分析了用户簇过程的半径或方差、SIR门限值、小基站密度和小基站功率对覆盖概率的影响，并且与三维用户均匀分布模型和二维用户簇分布模型的覆盖概率性能进行了比较。

1 系统模型

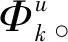
本文为三维异构蜂窝网络中的用户簇分布建模采用2种常见的泊松簇过程：Matern簇过程和Thomas簇过程[14]。

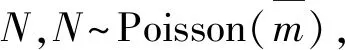
(1)

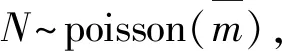
(2)

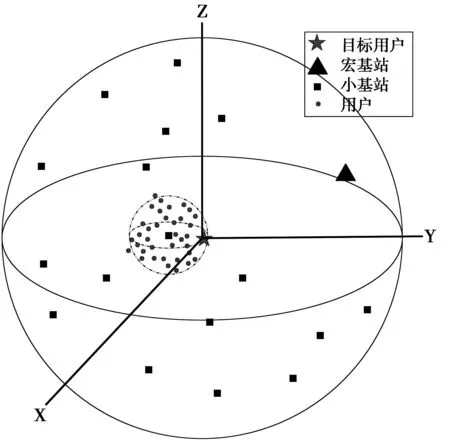
图1 三维异构蜂窝网络基站和用户分布的系统模型Fig.1 System model of base station and user distribution of three dimensional heterogeneous cellular network

2 性能分析

定义三维异构蜂窝网络的平均覆盖概率为Ρc(β)=Ρ{SIR≥β},β为预先定义的SIR门限值。

基于第1节给出的系统模型，服务基站位于x∈Φk处，定义目标用户的信号干扰比SIR为

(3)

定理1假设信号干扰比门限值为βk，用户接入提供最大信号干扰比的基站，则覆盖概率为

(4)

(4)式中，

(5)

证明：

(6)

(6)式中：步骤①是由于信道增益hx～exp(1)，步骤②是由于Φk相互独立。

(6)式中，

(7)

(7)式中：步骤(a)是因为{hy}是独立的指数随机变量；Gj(vk,j(x,y))是泊松点过程的概率密度函数。对 (6) 式进行同样的变换，可以得到定理1。

由定理1可以得到以下2个推论。

推论1当基站服从泊松点过程时，每层基站覆盖概率可以表示为

k∈K

(8)

(8)式中，Gj(vk,j(x,y))是泊松点过程的概率密度函数。

由文献[8]可以得到当j∈Κ时，密度为λ的泊松点过程的概率密度函数为

(9)

(10)

对于第0层基站，用户分布服从以基站为父节点的泊松簇过程。根据概率密度函数的定义，可以得到：

(11)

当用户服从Matern簇过程时，f0(y)由(1) 式给出；当用户服从Thomas簇过程时，f0(y)由(2) 式给出。

由于Φ0只有1个点，并且服从概率密度函数f0(x)，根据(4)式和(11)式，可以得到以下推论2。

推论2第0层的覆盖概率为

(12)

当用户服从Matern簇过程时，f0(x)由(1)式给出；当用户服从Thomas簇过程时，f0(x)由(2)式给出。

3 仿真结果与分析

表1 基本仿真参数Tab.1 Basic simulation parameters

图2分析了用户分布为Matern簇过程时，SIR门限值对三维异构蜂窝网络覆盖概率的影响，比较了覆盖概率的理论分析值与蒙特卡罗仿真值。从图2中可以看出，覆盖概率的理论分析值与蒙特卡罗仿真值一致。基于用户均匀分布模型的覆盖概率曲线是基于用户成簇分布模型的覆盖概率曲线下界，说明如果考虑用户成簇分布，网络性能更好，并且随着r从20 m增加到40 m，覆盖概率越来越低，说明用户簇半径越大，得到的覆盖概率越小。

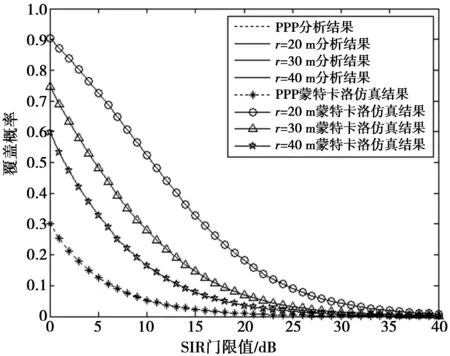
图2 用户分布为Matern簇过程时，SIR门限值对覆盖 概率的影响Fig.2 Coverage probability versus SIR threshold as the distribution of users is Matern cluster process

图3分析了用户分布为Thomas簇过程时，SIR门限值对三维异构蜂窝网络覆盖概率的影响，比较了覆盖概率的理论分析值与蒙特卡罗仿真值。从图3中可以看出，覆盖概率的理论分析值与蒙特卡洛仿真值一致，基于用户均匀分布模型得到的覆盖概率曲线是基于用户成簇分布模型的下界。并且随着方差σ从20增加到40，覆盖概率逐渐减小。由此可以说明，用户聚集离小基站越近，覆盖效果越好，符合实际网络。

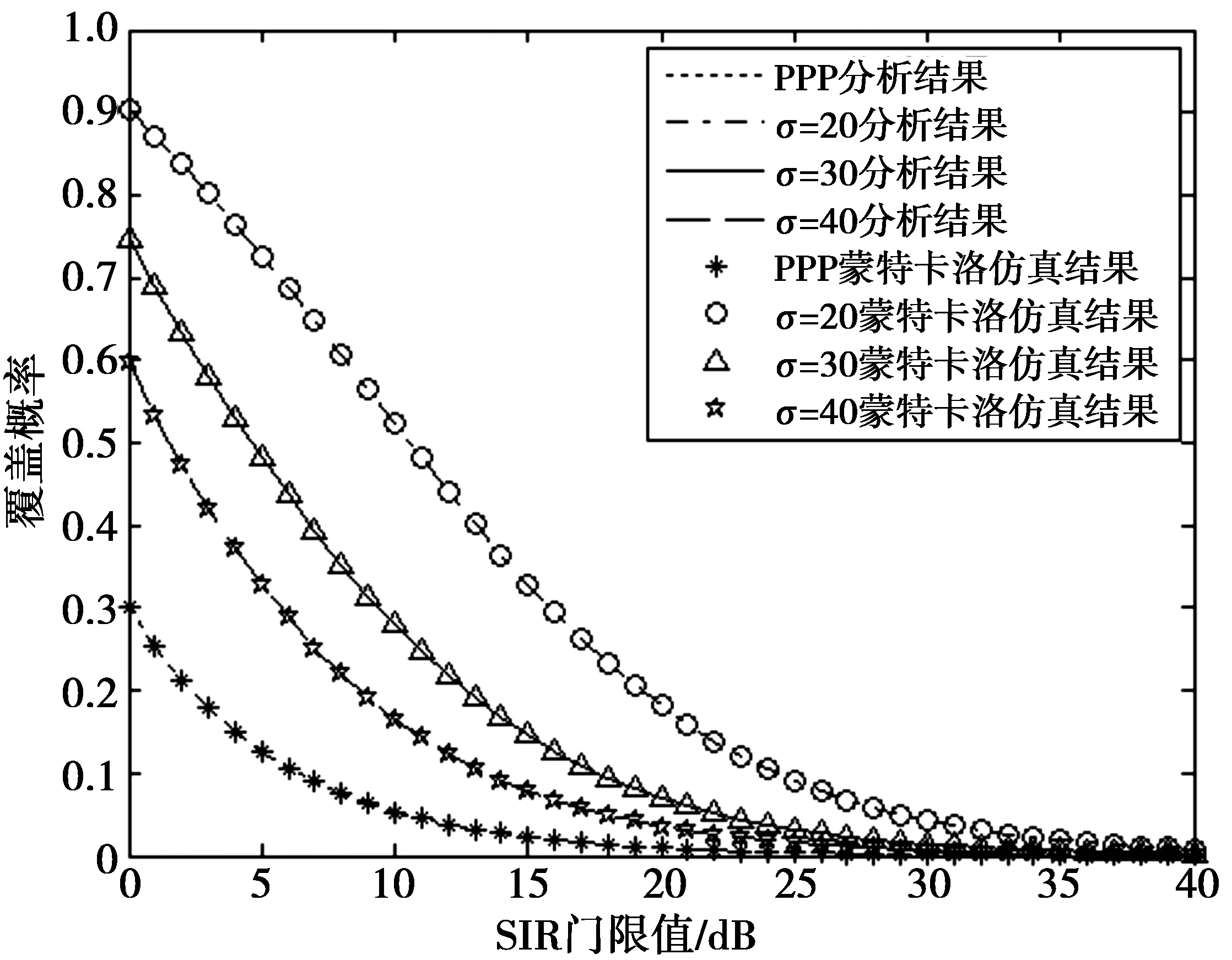
图3 用户分布为Thomas簇过程时，SIR门限值对覆盖 概率的影响Fig.3 Coverage probability versus SIR threshold as the distribution of users is Thomas cluster process

图4表示当β为0 dB，改变小基站与宏基站密度之比，用户分布为Matern簇过程时，小基站密度对覆盖概率的影响。从图4中可以看出，随着小基站与宏基站密度之比从0增大到2 000，覆盖概率逐渐减少。这就说明，当小基站密度增加时，干扰增大，覆盖概率减少。当r为40 m时，覆盖概率减少得最多，说明用户与小基站距离越远，受到其他基站的干扰越大。

图5表示当β为0 dB，改变小基站与宏基站密度之比，用户分布为Thomas簇过程时，小基站密度对覆盖概率的影响。从图5中可以看出，随着小基站密度增大，覆盖率逐渐减少。当σ从20增大到40，覆盖率越来越低，趋近于用户均匀分布的覆盖概率。将图5与图4进行比较，可以得知，用户分布为Thomas簇过程时得到的覆盖概率普遍小于用户分布为Matern簇过程的覆盖概率。

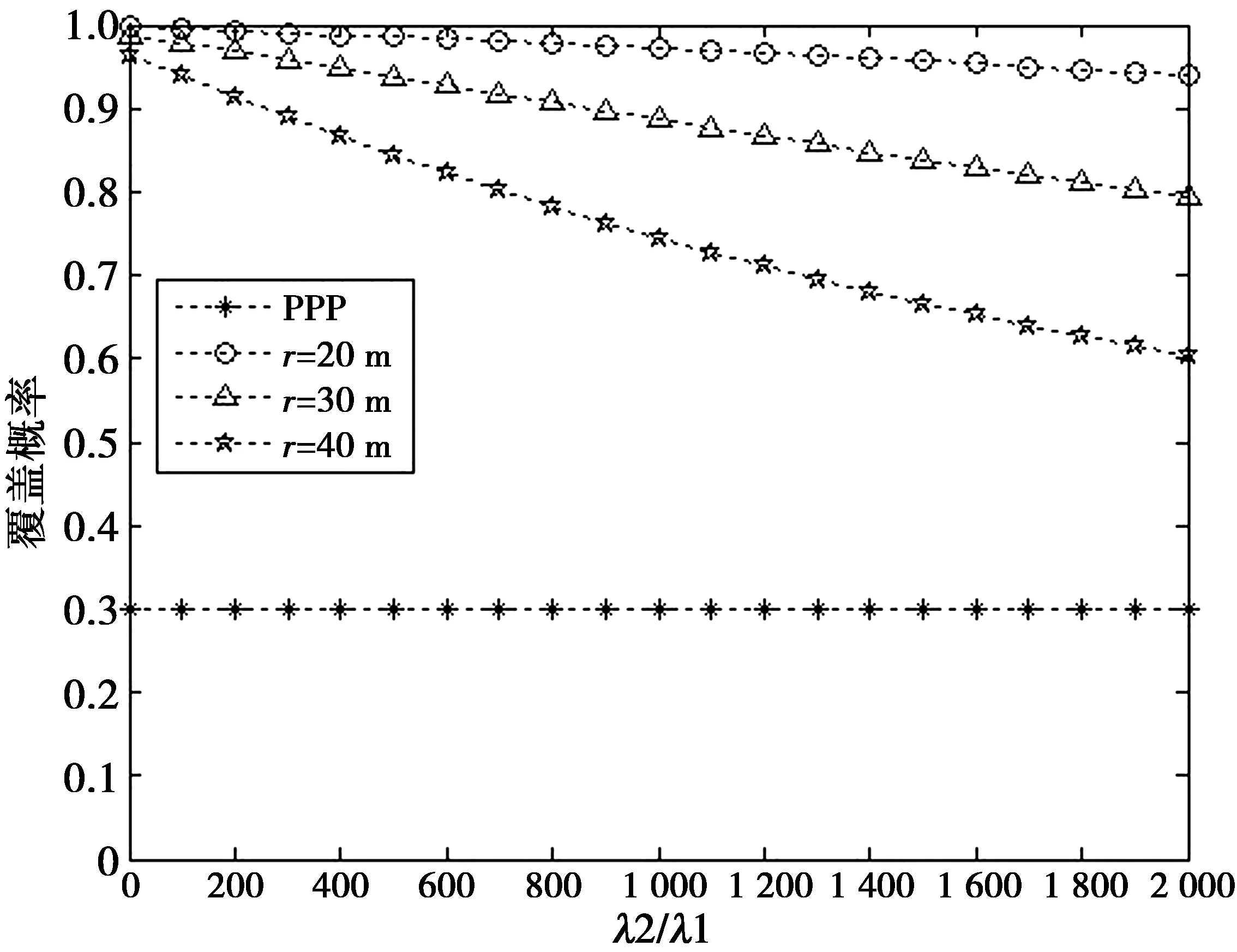
图4 用户分布为Matern簇过程时，小基站密度对覆盖 概率的影响Fig.4 Coverage probability versus small cell BS density as the distribution of users is Matern cluster process

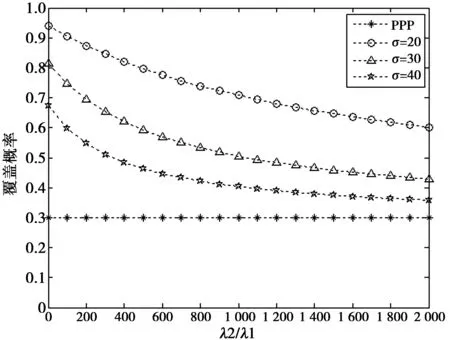
图5 用户分布为Thomas簇过程时，小基站密度对覆盖 概率的影响Fig.5 Coverage probability versus small cell BS density as the distribution of users is Thomas cluster process

图6表示当β为0 dB，改变小基站与宏基站功率之比，用户分布为Matern簇过程时，小基站功率对覆盖概率的影响。从图6中可以看出：当P2/P1小于-70 dB时，覆盖概率基本维持在0.3，与用户均匀分布得到的覆盖概率一致；当P2/P1在-70～-10 dB时，覆盖概率逐渐增大，且固定功率之比时，半径r越大，覆盖概率越大；当P2/P1大于-10 dB时，覆盖概率趋于饱和且达到最大值。

图7表示当β为0 dB，改变小基站与宏基站功率之比，用户分布为Thomas簇过程时，小基站功率对覆盖概率的影响。从图7中可以看出：当P2/P1小于-65 dB时，覆盖概率基本维持在0.3，与用户均匀分布得到的覆盖概率一致；当P2/P1在-65～-10 dB时，覆盖概率逐渐增大，且固定功率之比时，方差σ越大，覆盖概率越大；当P2/P1大于-10 dB时，覆盖率趋于饱和且达到最大值。与图6进行比较，用户分布为Thomas簇过程的覆盖概率依然小于用户分布为Matern簇过程的覆盖概率。

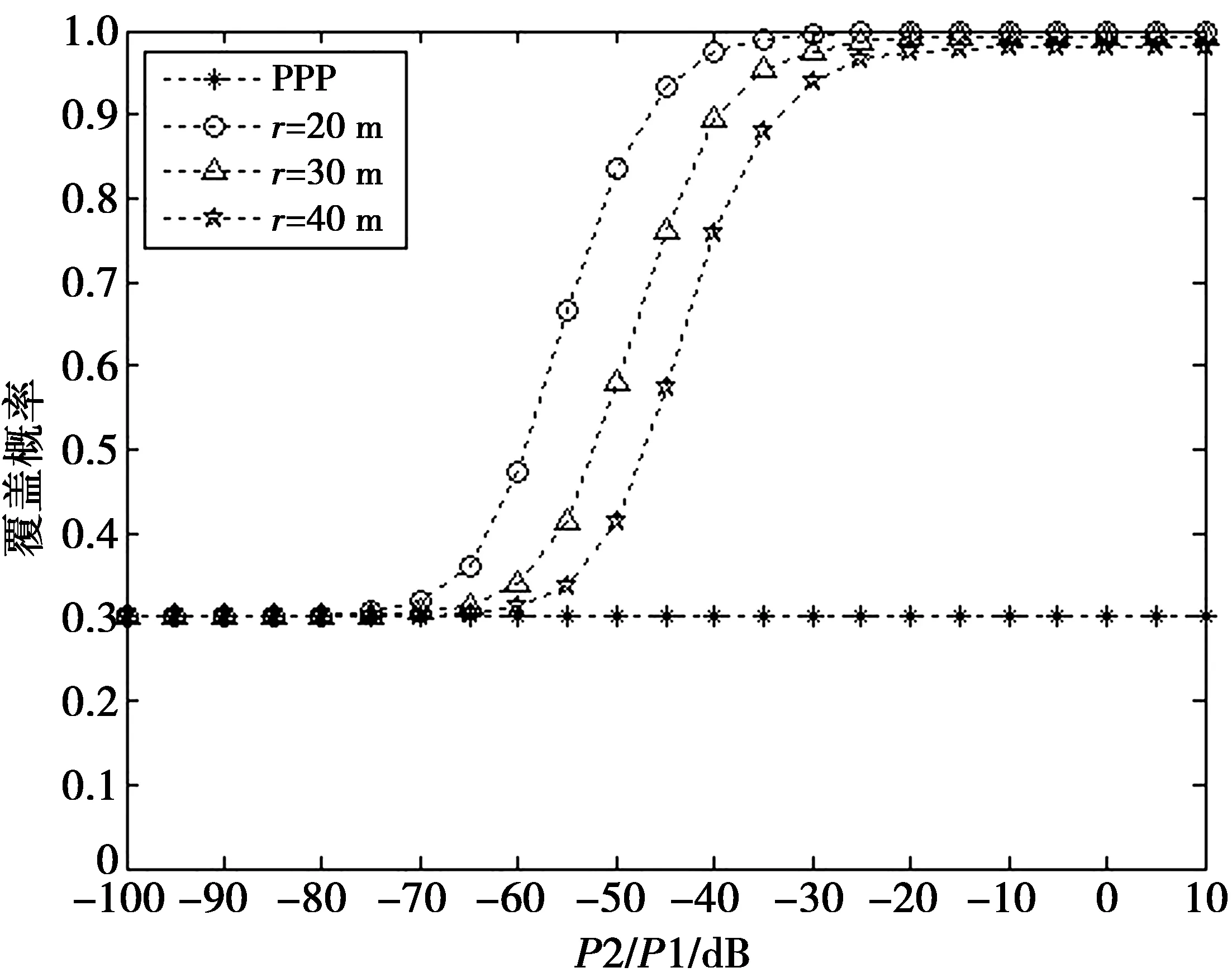
图6 用户分布为Matern簇过程时，小基站功率对覆盖 概率的影响Fig.6 Coverage probability versus small cell BS power as the distribution of users is Matern cluster process

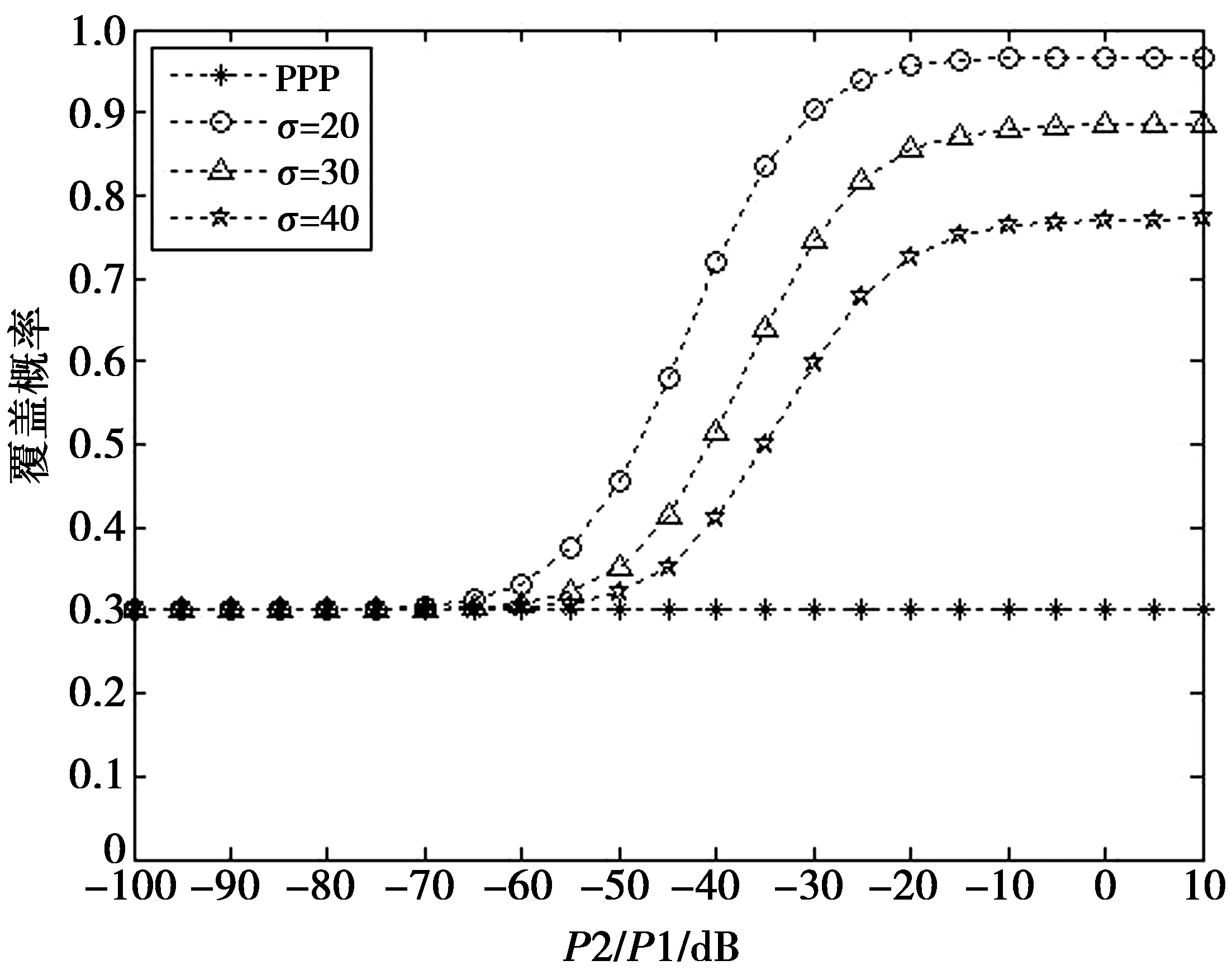
图7 用户分布为Thomas簇过程时，小基站功率对覆盖 概率的影响Fig.7 Coverage probability versus small cell BS power as the distribution of users is Thomas cluster process

图8对比了r为20 m和σ为20时，用户分布以小基站为父节点的簇过程二维模型和三维模型的覆盖概率。从图8中可以看出：当用户服从Matern簇过程时，三维模型得到的覆盖概率较高；当用户服从Thomas簇过程且门限值小于30 dB时，三维模型的覆盖概率较高；当门限值大于30 dB时，二维模型得到的覆盖概率略高。因为当r为20 m和σ为20时，目标用户接入同簇内小基站的概率更高，二维模型和三维模型的接收功率差别不大，而基于二维空间的泊松点过程模型忽略了高度对距离的影响，来自于其他基站的干扰就比三维模型大。因此，三维模型的覆盖概率比二维模型高。

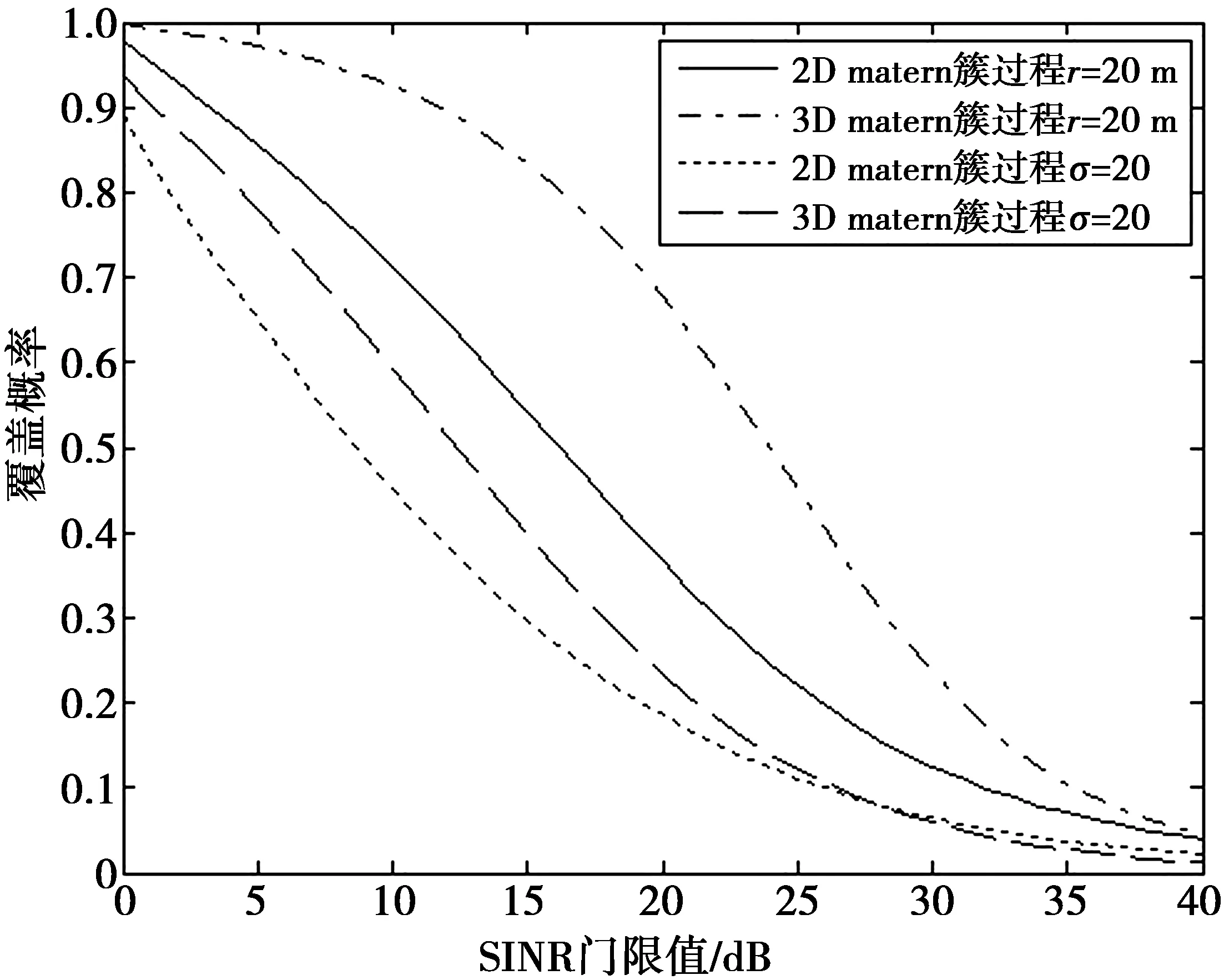
图8 二维模型与三维模型覆盖概率比较Fig.8 Comparison of coverage probability between two dimensional model and three dimensional model

4 总 结

本文提出了一种用户以小基站为中心成簇分布的三维异构蜂窝网络模型。在该模型基础上，用户接入提供最大信号干扰比的基站，得到了覆盖概率的分析结果，并通过蒙特卡罗仿真验证了理论结果的准确性。通过仿真结果得到以下结论：①与用户均匀分布模型相比，用户以小基站为中心的簇过程分布模型更适合于建模移动用户密集的异构蜂窝网络；②用户分布为簇过程时，半径的变化对于蜂窝网络性能有很大影响，簇过程半径越大，得到的覆盖概率越小；③用户服从Matern簇过程比Thomas簇过程得到的覆盖概率更大；④用户分布为簇过程时，三维模型比二维模型的网络性能好，得到的覆盖概率大。