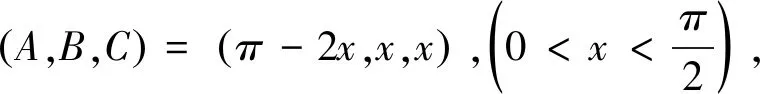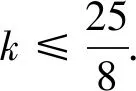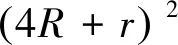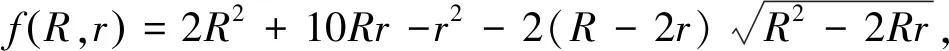关于Gordon不等式的加强
山东省威海职业学院艺术设计系
姜卫东 (邮编:264210)
本文约定: △ABC三边长分别为a、b、c,面积为△,s、R、r分别表示△ABC的半周长,外接圆半径和内切圆半径.
在△ABC中,有不等式
①
这是著名的Weisenbock不等式[1].
①已有很多种形式的加强,其中最著名的是费-哈不等式
②
1966年,Gordon给出了如下不等式
③
注意到文[2]已给出③的如下加强
bc+ca+ab≥18Rr
④
本文主要讨论③和④的加强问题.
1 Bencze公开问题的解决
考虑到④的加强,最近,罗马尼亚的M. Bencze在[3]中提出如下的公开问题:
OQ5302在△ABC中,求最佳的λ,使下面不等式成立.
bc+ca+ab≥18Rr+λ[(a-b)2+(b-c)2+(c-a)2]
⑤
下面给出⑤的解答.
由abc=4Rrs,a+b+c=2s,
可知,⑤等价于
⑥
设a=b=1,c=x,则易知0 定理1 在在△ABC中,有 ⑦ 证明由三角形中熟知的恒等式 bc+ca+ab=s2+4Rr+r2, ∑a2=2(s2-4Rr-r2), ⑦等价于s2≥16Rr-5r2. 这就是Gerretsen不等式,从而⑦成立. 最近,安振平老师在其新浪博客中提出了③的另一种加强[4]: 问题4585在△ABC中,有 ⑧ 由⑧的形式,一个很自然的问题是:求使下式成立的最大的k: ⑨ 简单的计算可知,上式等价于 ⑩ 则⑩变形为 ○11 定理2在△ABC中,有 ○12 证明由三角形中熟知的恒等式 bc+ca+ab=s2+4Rr+r2,△=rs. 可知○12 等价于 (s2+4Rr+r2)2≥25Rrs2-2r2s2,即 H(s2)=s4-(17Rr-4r2)s2 ○13 由已知的不等式(见[1]的5.9和5.10) s2≥f(R,r)≥16Rr-5r2.其中 2(16Rr-5r2)-(17Rr-4r2)=15Rr-6r2>0. 从而有 最后一步由欧拉不等式R≥2r可知,从而定理2成立. 特别的,在⑨中令k=2,即得⑧.
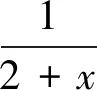
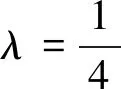
2 安振平的一个不等式的最优化加强