变精度与程度“逻辑或”多粒度粗糙集

汪小燕， 郭云婷， 申元霞

（安徽工业大学 计算机科学与技术学院，安徽 马鞍山 243032）

粗糙集理论[1]是Pawlak 等学者在1982年提出的处理不确定、不精确和不完全数据的一种新的数学工具，主要研究内容是属性约简[2]和规则提取。多粒度粗糙集[3-6]作为一种新型的多视角数据分析方法，可以从多个粒度空间对目标概念进行近似逼近，使得边界区域减少，目标概念的表示精度得到提高，并且与其他处理不确定知识的理论结合，受到了学者们的广泛关注。文献[7]将多粒度粗糙集扩展到变精度多粒度粗糙集，文献[8]将其扩展到程度多粒度粗糙集，文献[9]将其扩展到可变多粒度粗糙集，众多学者更是从模糊关系[10]、不完备信息系统[11-13]、邻域关系[14]、证据理论[15]等角度对多粒度粗糙集进行了深入的扩展，这些研究工作促进了多粒度粗糙集理论和应用的发展。文献[16]提出了基于等价关系的精度与程度“逻辑或”粗糙集模型，融合了相对量化信息和绝对量化信息。文中针对不完备信息系统，将精度与程度“逻辑或”粗糙集扩展到基于限制容差关系的不完备信息系统中，融入多粒度思想，提出基于限制容差关系的变精度与程度“逻辑或”多粒度粗糙集，包括“逻辑或”乐观多粒度粗糙集和“逻辑或”悲观多粒度粗糙集，研究“逻辑或”乐观、悲观多粒度粗糙集的性质和相互之间的关系，并通过实例分析和实验验证了模型及所提出理论的有效性。

1 基本概念

1.1 限制容差关系

限制容差关系是不完备信息系统中，用于对象分类的一种重要的二元关系，可以使分类更加合理。

定义1[17]假定不完备信息系统IS＝〈U，AT，V，f〉及U 上定义的二元关系L（限制容差关系），对于A⊆AT，则

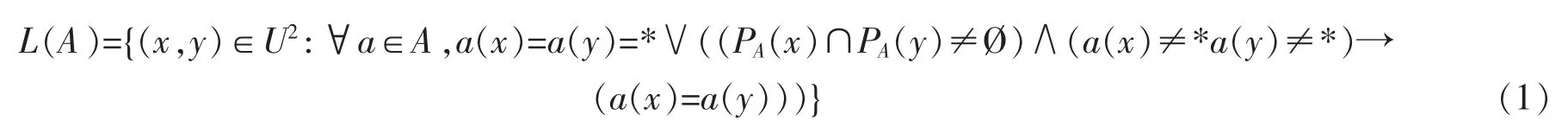
其中PA（x）＝{a|a∈A∧a（x）≠*}。

定义2[17]设不完备信息系统IS＝〈U，AT，V，f〉，对于∀X⊆U，A⊆AT，X 在限制容差关系L（A）的下近似、上近似分别为

其中LA（x）是x 的限制容差类。

1.2 基于限制容差关系的多粒度粗糙集

在不完备信息系统中，文献[18]结合限制容差关系，提出乐观多粒度粗糙集和悲观多粒度粗糙集的下近似、上近似定义。

定义3[18]设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的乐观多粒度粗糙集下近似、上近似分别定义为

定义4[18]设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的悲观多粒度粗糙集下近似、上近似分别定义为

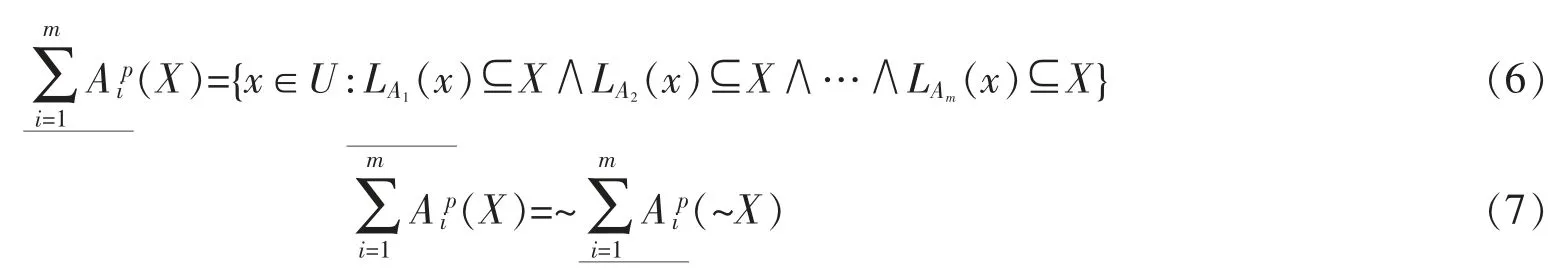
1.3 基于等价关系的精度与程度“逻辑或”粗糙集

变精度粗糙集模型和程度粗糙集模型是两类重要的粗糙集扩展模型，其中精度反映了近似空间的相对量化信息，而程度则刻画了近似空间的绝对量化信息。文献[16]为了融合这两种特性，提出精度与程度“逻辑或”粗糙集。

定义5[16]设信息系统S＝〈U，AT〉，A⊆AT，k 为任意自然数，β∈[0，0.5），∀X⊆U，X 关于A 依精度1-β、程度k 的逻辑或下、上近似算子分别定义为

2 基于限制容差关系的变精度与程度“逻辑或”粗糙集

程度粗糙集存在当[x]A∩X=Ø，|[x]A|-|[x]A∩X|≤k 可能成立，即的问题，现结合限制容差关系，在下近似中增加约束条件，构建基于限制容差关系的变精度与程度“逻辑或”模型。

定义6设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，在限制容差关系L（A）下，X 变精度与程度“逻辑或”粗糙集的下近似、上近似分别定义为

3 基于限制容差关系的变精度与程度“逻辑或”多粒度粗糙集

为了进一步对多粒度粗糙集进行拓展，在定义6 的基础上，融入多粒度思想，提出变精度与程度“逻辑或”多粒度粗糙集模型。

定义7设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的变精度与程度“逻辑或”乐观多粒度粗糙集下近似、上近似分别定义为

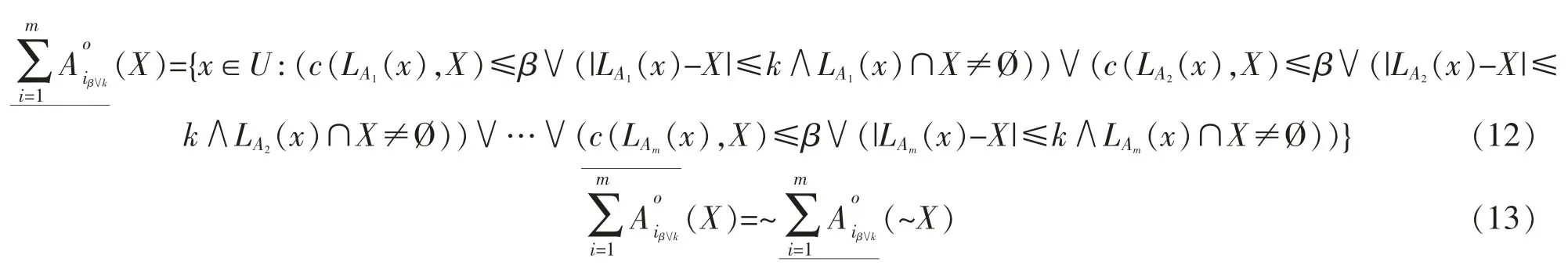
定义8设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的变精度与程度“逻辑或”悲观多粒度粗糙集下近似、上近似分别定义为

说明在基于限制容差关系的变精度与程度“逻辑或”乐观多粒度粗糙集中，要求对象至少有一个粒度层次上的限制容差类满足c（LAi（x），X）≤β∨（|LAi（x）-X|≤k∧LAi（x）∩X≠Ø），则定义为其下近似。在基于限制容差关系的变精度与程度“逻辑或”悲观多粒度粗糙集中，要求对象所有粒度层次上的限制容差类满足c（LAi（x），X）≤β∨（|LAi（x）-X|≤k∧LAi（x）∩X≠Ø），则定义为其下近似。

定理1设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的变精度与程度“逻辑或”乐观多粒度粗糙集有如下性质：

（2）k1、k2为任意自然数，β1、β2∈[0，0.5），若k1≤k2、β1≤β2，则

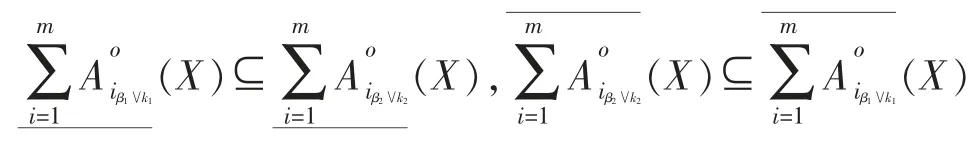
综上所述，在建筑工程项目的设计过程中运用BIM技术，可以有效缩短工期，从而减少施工成本。同时还会促进建筑设计企业工作水平的不断上升，从而在保证建筑设计企业经济效益的同时获得社会效益，保证其可持续性发展。

证明

（1）∀X⊆U，∀Ai∈A，由于LAi（x）⊆U，故有c（LAi（x），U）=0，从而对于β∈[0，0.5），显然有c（LAi（x），U）≤β 成立。或者|LAi（x）-U|=0，从而对于任意自然数k，显然有|LAi（x）-U|≤k∧LAi（x）∩U≠Ø 成立，因此，

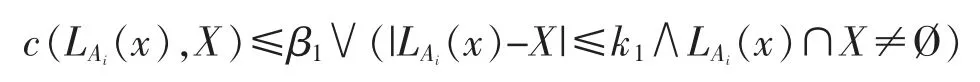
又由于k1≤k2、β1≤β2，从而c（LAi（x），X）≤β2∨（|LAi（x）-X|≤k2∧LAi（x）∩X≠Ø），因此，即有由定义7 得，

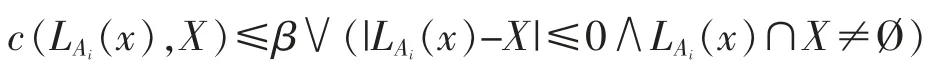
若c（LAi（x），X）≤β 成立，则若|LAi（x）-X|≤0 成立，则必有LAi（x）⊆X，此时c（LAi（x），X）=0，从而对于β∈[0，0.5），显然c（LAi（x），X）≤β 成立，则因此，反之，若则至少存在某个Ai∈{A1，A2，…，Am}，使得c（LAi（x），X）≤β，由定义7 知即有所以综合有由定义7 知，又由第一部分结论知故有

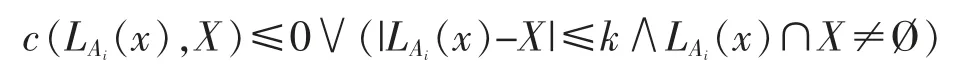
若c（LAi（x），X）≤0 成立，此时|LAi（x）|-|LAi（x）∩X|≤0，从而对于任意自然数k，显然|LAi（x）|-|LAi（x）∩X|≤k，则若|LAi（x）-X|≤k 成立，又因为LAi（x）∩X≠Ø，显然|LAi（x）|-|LAi（x）∩X|≤k， 则因此，反之，若则至少存在某个Ai∈{A1，A2，…，Am}，使得|LAi（x）|-|LAi（x）∩X|≤k，又因为LAi（x）∩X≠Ø，故|LAi（x）-X|≤k，从而由定义7 可知即有所以综合有由定义7 可知，又由第一部分结论知故有

定理2设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，在限制容差关系族L（A1），L（A2），…，L（Am）下的变精度与程度“逻辑或”悲观多粒度粗糙集有如下性质：

（2）k1、k2为任意自然数，β1、β2∈[0，0.5），若k1≤k2、β1≤β2，则

定理2 的证明类似于定理1 的证明。

定理1 性质（3）和定理2 性质（3）说明，当k=0，变精度与程度“逻辑或”乐（悲）观多粒度粗糙集就退化为变精度乐（悲）观多粒度粗糙集。定理1 性质（4）和定理2 性质（4）说明，当β=0，变精度与程度“逻辑或”乐（悲）观多粒度粗糙集就退化为程度乐（悲）观多粒度粗糙集。

定理3设不完备信息系统IS＝〈U，AT，V，f〉，A={A1，A2，…，Am}是AT 的m 个属性子集，k 为任意自然数，β∈[0，0.5），∀X⊆U，则变精度与程度“逻辑或”乐观和悲观多粒度粗糙集的关系如下：

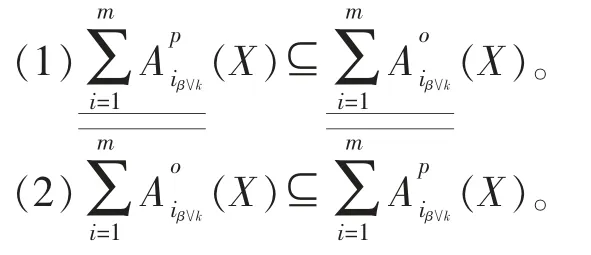
证明由定义7 和定义8 可证。

4 实例分析

设不完备决策系统IS＝〈U，AT，V，f〉，其中对象集U={x1，x2，…，x8}，条件属性AT={c1，c2，c3，c4}，d 为决策属性，取β=0.3，k=1。。

由表1[4]知U/IND（{d}）＝{D1，D2}，其中D1＝{x1，x3，x4，x6}，D2＝{x2，x5，x7，x8}，设决策信息系统的属性子集族如下

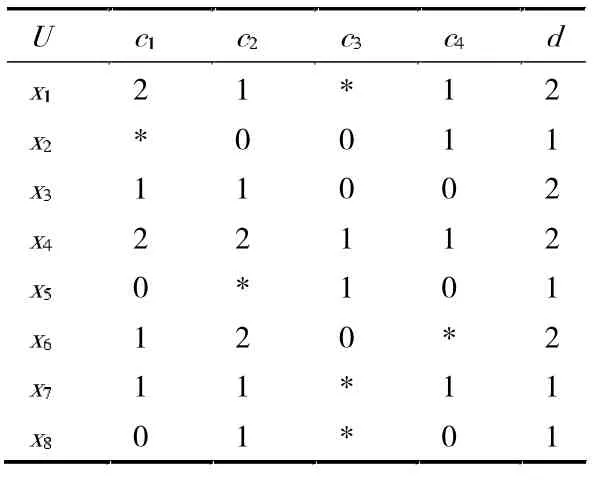
表1 不完备决策系统

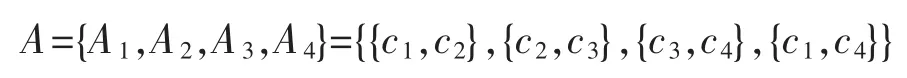
分别计算出变精度与程度“逻辑或”乐观多粒度粗糙集、变精度与程度“逻辑或”悲观多粒度粗糙集的下近似和上近似：

（1）决策类D1的下近似和上近似分别为

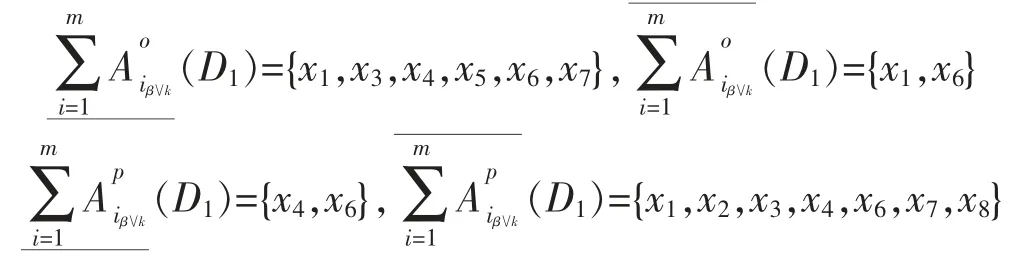
（2）决策类D2的下近似和上近似分别为

由计算结果知以下公式成立

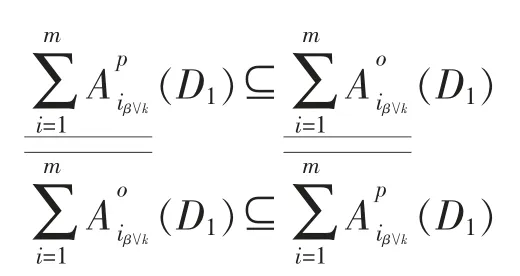
同理，对D2也有以上公式成立。

为了验证基于限制容差关系的变精度与程度“逻辑或”多粒度粗糙集的性质，选用UCI 机器学习数据集上Zoo 和Tic-tac-toe （http：// archive.Ics.uci.edu/ml/machine-learning-databases/） 进行仿真实验，数据描述见表2。

首先对数据处理，使该系统存在缺失值，根据决策属性将Zoo 分为7 个决策类D1，D2，D3，D4，D5，D6，D7。文中选取属性集合A={A1，A2，A3}，令第1～6 个属性为A1，第6～11 个属性为A2，第11～16 个属性为A3，在β=0.3，k=1 的前提下，分别计算变精度与程度“逻辑或”乐观多粒度粗糙集、变精度与程度“逻辑或”悲观多粒度粗糙集的下、上近似的样本个数，见表3。类似可得Tic-tac-toe 的结果，见表4。

表2 数据描述

表3 Zoo数据集上的结果

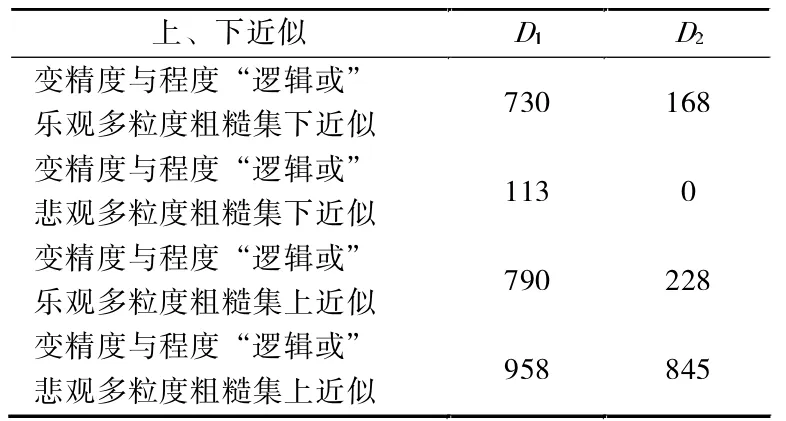
表4 Tic-tac-toe 数据集上的结果

在Zoo数据集上有7 个决策类，对于每个决策类，从表3 中可以看出，变精度与程度“逻辑或”悲观多粒度粗糙集下近似对象个数都少于变精度与程度“逻辑或”乐观多粒度粗糙集下近似对象个数。而变精度与程度“逻辑或”悲观多粒度粗糙集上近似对象个数都多于变精度与程度“逻辑或”乐观多粒度粗糙集上近似对象个数，在表4 中Tic-tac-toe 数据集上也同样存在这样的结论。实验结果表明，变精度与程度“逻辑或”乐观多粒度粗糙集和变精度与程度“逻辑或”悲观多粒度粗糙集的上、下近似之间存在包含关系，从实验角度验证了定理的正确性。

5 结语

从精度与程度“逻辑或”的角度出发，基于限制容差关系提出变精度与程度“逻辑或”乐观多粒度、变精度与程度“逻辑或”悲观多粒度粗糙集模型。该模型可通过调节阈值β、k，使分类更加准确。接下来的工作将研究变精度与程度“逻辑或”多粒度粗糙集的约简和决策规则的获取等问题。