扇形气膜孔冷却效率的数值模拟
王晓春, 李 娟
(苏州科技大学 环境科学与工程学院,江苏 苏州 215009)
为了提高战斗机的性能,战斗机不断地向大推力、高速度、高机动性能的方向发展。因此,燃气透平的进口温度需要不断上升。目前,先进透平燃气进口温度已经远远超过现有透平材料的熔点。为了保证透平高温部件的安全运行及合理寿命,现有航空发动机端壁中广泛采用了气膜冷却技术。气膜冷却特性的控制受到很多因素的影响,例如气膜孔的几何参数、叶片的几何参数、孔的气动参数等。
在气膜孔几何形状设计方面,Goldstein 等人[1]可能是最先关注不同气膜孔形状导致的冷却特性差异,随后人们研究了多种扩张气膜孔结构。Wittig 等人[2]、Thole 等人[3]、Gritsch 等人[4]先后比较了圆柱形、出口横向扩张、横向向前扩张孔的冷却特性。张玲等人[5]研究了气膜孔轴向倾角和展向倾角对端壁冷却效率的影响。在众多气膜孔结构中,扇形扩张气膜孔结构的气膜覆盖面积较大,因而受到广泛的关注和研究[6-7]。笔者此前的研究中也比较了三种扇形气膜孔结构的冷却特性[8]。为清晰的显示扇形气膜孔的气膜覆盖范围,对绝热壁面假设下的气膜冷却效率进行了数值模拟,结果表明,冷却流在气膜孔下游逐渐分叉成两股,导致覆盖面积变小,气膜孔下游不能被很好地冷却。
在气膜孔的冷却效率研究中,广泛采用实验获得表面冷却效率云图。例如:翟颖妮等人[9]采用热色液晶技术测量了倾斜角圆柱孔、水滴孔以及曲面簸箕孔的气膜冷却特性;常艳等人[10]利用红外热像测温技术研究了带有突片结构的气膜孔的气膜冷却特性;李广超等人[11]也利用红外技术测量了双出口气膜孔的冷却效率。随着计算机性能的提升,数值模拟方法因其经济且高效的特性在众多领域得到广泛应用[12-13]。笔者通过数值模拟的方法获得了气膜孔表面冷却效率云图,并以此为基础,尝试通过定量的方式来描述冷却效率,并提出了精度较高的拟合公式,用公式定量描述冷却效率的方法更便于定量比较不同结构气膜孔的冷却效率。
1 研究模型及方法
1.1 气膜孔结构
图1 展示了数值模拟所采用扇形气膜孔结构。该气膜孔由纯圆柱进口和侧向扩张出口两部分组成。纯圆柱部分的特征直径D 为0.6 mm,圆柱轴线与气膜孔出口平面的夹角为30°,侧向扩张角为14°。
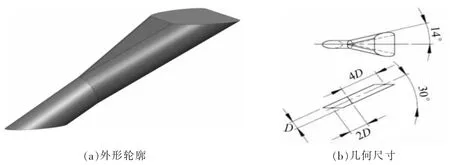
图1 扇形气膜孔几何结构
1.2 气膜冷却的数值模型
数值模拟的研究区域如图2 所示。图2(a)显示了固壁绝热条件下的研究区域:主流域、冷却流域和气膜孔。图2(b)展示了流固耦合条件下的模拟区域,比图2(a)多了固体壁面域。图2(c)给出模拟区域的几何尺寸。研究区域的稳态流动和换热模型可以用可压缩雷诺时均的Navier-Stokes(RNS)方程求解。该方程可用张量表示成如下形式

采用商业软件ANSYS CFX 14.0 对该方程进行数值计算。选择RNG k-ε 湍流模型。该软件计算时利用有限容积法,模拟区域划分和尺寸介绍如图2 所示。计算网格利用商业软件ANSYS ICEM 14.0 生成。气膜孔采用六面体O 型网格,其他区域采用普通六面体网格。对壁面附近网格加密,使边界层部分第一层网格的y+值全部小于1。通过对网格加密来验证无关性,加密前后,气膜孔附近的平均温度偏差小于3%,由此认为加密后的网格已经符合要求,作为后面模拟研究中采用的网格。
2 结果及讨论
2.1 扇形气膜孔出口的冷却流分叉现象
为了研究单纯由气膜孔引起的冷却效率差异,采用绝热壁面假设,忽略固壁导热的影响,采用商业软件ANSYS CFX 对图2(a)所示的研究区域进行数值模拟。主流和冷却流均采用理想气体。模拟工况的边界条件设置如下:主流入口速度V∞设为120 m·s-1,温度T∞为900 K,主流入口雷诺数Re 为11 988(特征长度选主流通道入口的水力直径);冷气入口温度Tc为486 K,吹风比(BR)分别为0.5、1.0、1.5、2.0、3.0,相应的冷气入口速度Vc分别为0.256、0.512、0.768、1.024、1.536 m·s-1;除进出口外,研究区域所有表面均设置为绝热表面。吹风比的定义如下

冷却后的壁面温度分布如图3 所示。图3 中标尺最大最小值为各自温度分布图的最大最小值。可以发现:(1)在气膜孔的出口区域,冷气有两个最小值区域,说明冷气在出口处已经分叉成两股。同时,随着吹风比的增加这种分叉更加明显。(2)在气膜孔出口下游区域,冷气明显分成了两股,吹风比越大,这种分叉程度越显著。最期望被冷却的孔中心的下游区域,反而变成局部高温。(3)吹风比从0.5 增加到1.5 时,气膜孔下游区域温度明显降低。此时增加冷气量,会起到比较好的冷却效果。吹风比从1.5 增加到2.0 时,温度变化不明显。吹风比从2.0 增加到3.0 时可以发现,气膜孔下游区域温度反而上升。因而,扇形气膜孔在吹风比为1.5时具有最佳的冷却效果。
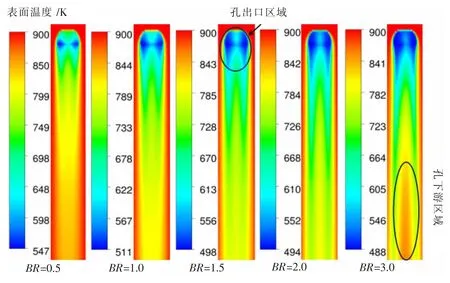
图3 不同吹风比下扇形气膜孔冷却效果比较
2.2 定量描述气膜冷却效率
为了研究固体壁面加入气膜冷却后的综合冷却效果,选择图2(b)所示模型为研究对象。主流和冷却流工质仍采用理想气体。由于固体导热对综合冷却效果影响很大[8],所以选取7 种不同导热率k(60.5、36.0、15.1、3.98、0.58、0.15、0.058 W·(m·K)-1)的工况进行数值模拟。模拟边界条件的设置如下:主流入口速度V∞设为120 m·s-1, 温度T∞为900 K, 主流入口雷诺数Re 为11 988; 冷气入口温度Tc为486 K, 速度Vc为1.024 m·s-1(相应的吹风比为2);主流和冷却流通道侧壁面设为绝热。
为定量描述气膜冷却效率,在固壁表面选取了6 个特征位置,如图4 所示。固壁表面气膜孔出口下游方向设为x 方向,气膜孔的圆柱轴线与固壁表面的交点设为x轴的原点,6 个特征位置分别在x 轴上的坐标为1D、4D、8D、12D、16D、20D 处。
通过数值模拟,得到7 种导热率下,固壁表面的温度分布Tw,进而可以算出6 个特征位置的冷却效率。这里的冷却效率为综合冷却效率,公式如下

固壁温度Tw与研究位置x 和固壁导热率k 有关,研究中,常采用毕渥数(Bi)描述导热率的变化,因而,冷却效率可以表示成

如果选择固定位置的x,那么气膜冷却效率将会是毕渥数的函数即

这里Bi 定义如下

其中L 表示固体壁面的厚度,1.8 mm;h 为固体表面的对流换热系数,由ANSYS CFX 计算获得。
笔者对6 个特征位置的冷却效率进行拟合,公式(7)在6 个特征点均可以得到比较理想的拟合结果。

式中:A、C1、C2、D1、D2是拟合方程的拟合系数。图5 给出了6 个特征位置的拟合曲线。
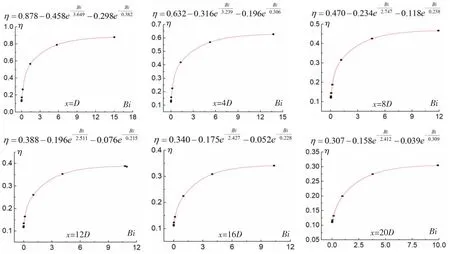
图5 特征位置冷却效率与毕渥数的关系
此外利用标准差分进化算法,对7 种导热率工况下6 个特征位置的数值模拟结果进行拟合,可以得到如下的拟合公式
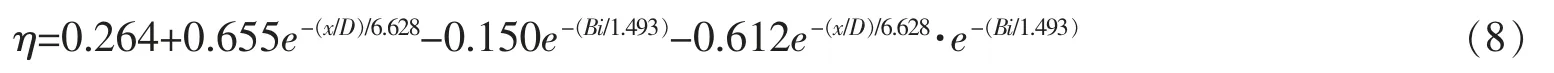
根据拟合公式(7)和(8),当端壁导热率趋于无穷大,即毕渥数趋于0 时,气膜冷却效率具有最小值;当端壁导热率趋于0,即毕渥数趋于无穷大时,气膜冷却效率具有最大值。变化趋势与实际相符合。同时,利用公式(7)(如图5 所示)和公式(8)所得7 种导热率工况下6 个特征位置的计算值,与采用ANSYS CFX 模拟值的最大偏差小于5.2%。
3 结语
通过数值模拟方法研究了扇形气膜孔的冷却特性。研究发现,冷气在气膜孔的出口区域分叉成两股,随着吹风比的增加这种分叉特征更加明显。冷气分叉使最期望被冷却的孔中心的下游区域,反而变成局部高温。考虑到冷气分叉的特征,发现在吹风比为1.5 时具有最佳冷却效果。
根据数值模拟结果,提出用拟合公式来描述气膜冷却效率。同时提出精度较高的拟合公式形式。利用数学公式η=η(x,Bi)来描述冷却效率的方法不仅形式简洁,同时更便于定量比较不同气膜孔的冷却效率,有助于改进气膜孔设计。
———《扇形的认识》教学廖

