曲线拟合算法对光纤光栅传感解调性能的影响研究*
李 宁,王 东,王 宇,白 清,周慧栋,靳宝全,2*
(1.太原理工大学新型传感器与智能控制教育部与山西省重点实验室,太原 030024;2.煤与煤层气共采国家重点实验室,山西 晋城 048012)
光纤布拉格光栅FBG(Fiber Bragg Grating)传感器是一种无源传感器,它具有体积小、精度高、抗电磁干扰等优点,可以测量温度、应变等多种参数,因此被广泛应用于土木工程、航空航天、精密仪器等领域[1-3]。光纤布拉格光栅解调系统是通过测量FBG中心波长的偏移量来检测外界参数的变化量。因此,如何准确测量FBG中心波长偏移量是解调系统的关键,但是由于噪声等因素存在会影响寻峰的精度[4]。通常可以采用曲线拟合算法来提高寻峰精度,常见的曲线拟合算法有质心法、一般多项式拟合、遗传算法、三次样条插值、高斯拟合、高斯-非线性拟合等[5-7]。质心法、一般多项式拟合计算简单,但是解调精度低、抗噪性能差。遗传算法、高斯-非线性拟合算法精度较高,但是比较依赖初始值的确定,需要在前期进行大量的实验计算[8]。高斯拟合算法与三次样条插值算法精度较高,应用广泛。因此,本文对比高斯拟合算法与三次样条插值算法,分析两种拟合算法对寻峰精度的影响,搭建光纤布拉格光栅解调系统进行实验验证。
1 光纤布拉格光栅解调原理
FBG传感器是一种波长编码型传感器,根据耦合模理论[9],其中心波长公式为:
λB=2nΛ1
(1)
式中:n为FBG有效折射率,Λ1为栅格周期。当外界温度与应变发生变化时会引起FBG有效折射率和栅格周期的改变,从而导致中心波长的偏移。当温度保持不变,FBG只受应变作用时,中心波长与应变的关系可表达为:
(2)
式中:Δλ为中心波长偏移量,u为泊松比,Δε为应变量。因此,通过测量FBG中心波长的偏移量即可推测出应变的变化量。光纤布拉格光栅解调系统如图1所示,ASE光源发出宽带光,经过隔离器进入可调谐F-P滤波器中进行滤波处理,然后通过1×2耦合器进入到参考光路与传感光路中,参考光路由 F-P 标准具与参考光栅组成,用于标定FBG中心波长。传感光路与参考光路的反射信号经过光电探测器后,经采集卡传输至上位机,在上位机中进行滤波、曲线拟合等数据处理,实现FBG中心波长以及被测物理量的解调。
2.1 数字低通滤波
解调系统在实际解调中由于内部器件以及外界环境的影响,导致反射信号中存在噪声,影响寻峰精度。为减少噪声对寻峰精度的影响,在解调前需要对反射信号进行必要的滤波处理,消除由噪声信号引起的误差[10-11]。本文选择算法灵活、适应性强的数字低通滤波,其表达式为:
Yn=qXn+(1-q)Yn-1
(3)
式中:q为时间常数,实际取决于滤波时间常数和采样周期;Xn为第n次采样时的滤波器输入;Yn为第n次采样时滤波器输出。数字低通滤波效果如图2所示,经过数字低通滤波后,去除了反射信号中的毛刺和假峰,使反射信号曲线更为平滑。
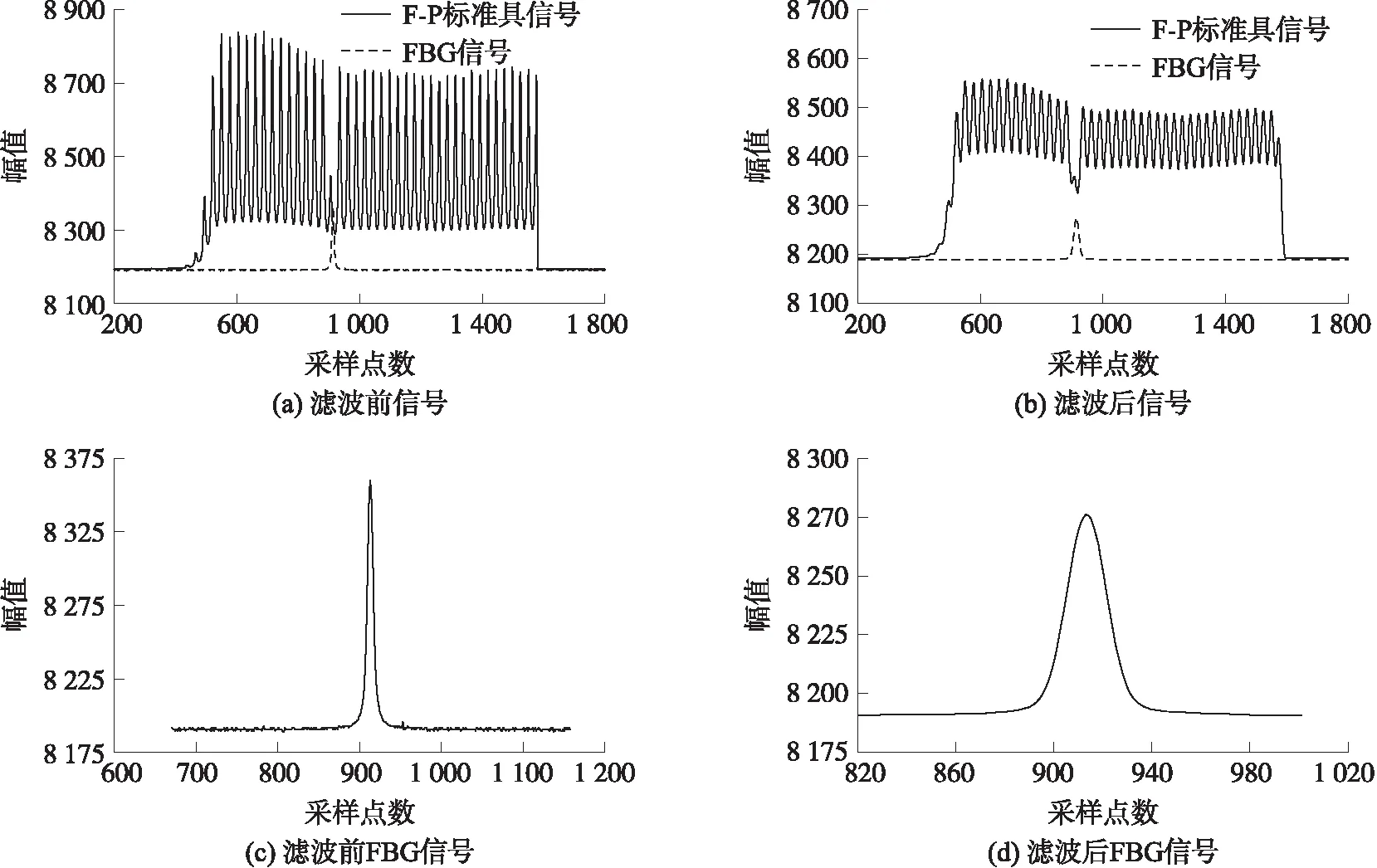
图2 数字低通滤波前后对比
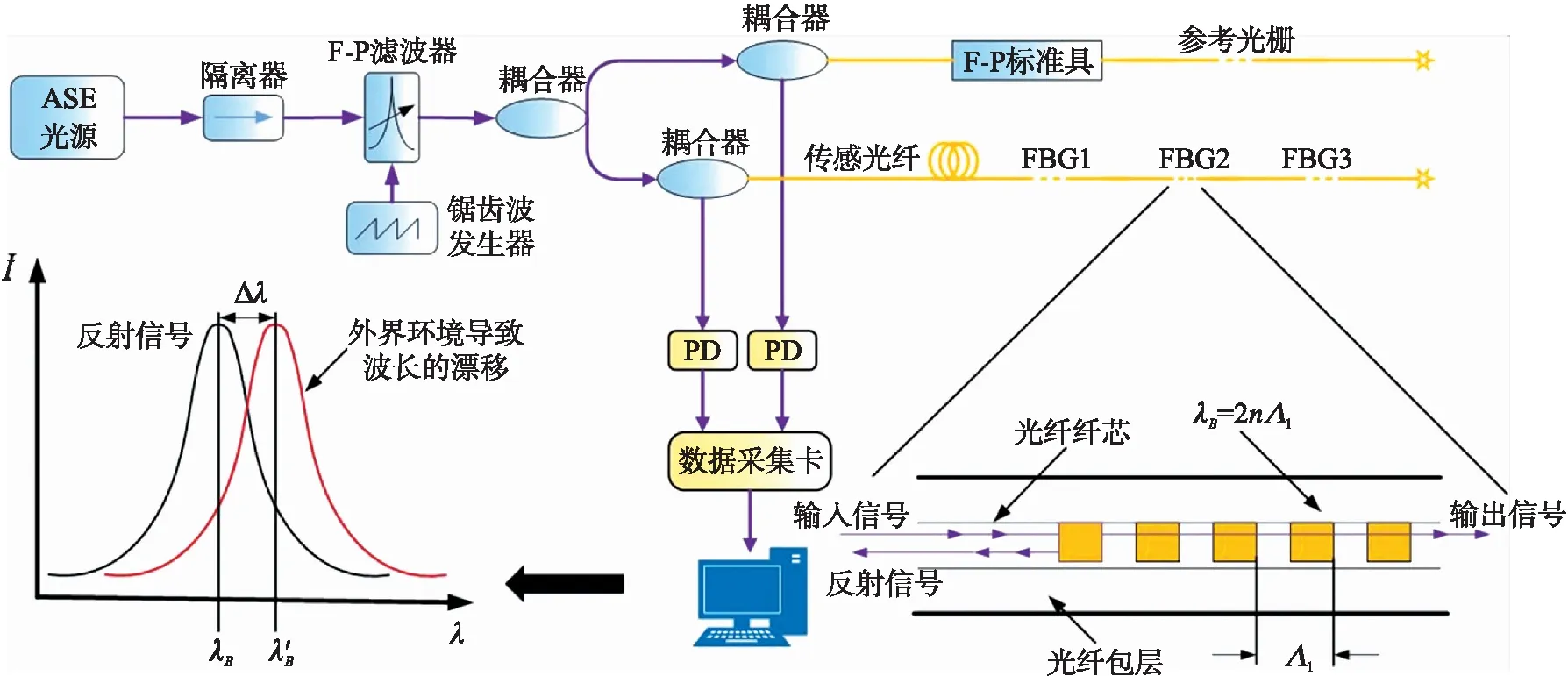
图1 光纤布拉格光栅解调系统原理
2.2 曲线拟合算法
数字低通滤波可以去除反射信号中的噪声,但是对于寻峰精度的提升有限。为了进一步提高系统的寻峰精度,可以采用曲线拟合算法对中心波长进行拟合。本文对高斯拟合算法与三次样条插值算法进行详细比较,选取更合适的拟合算法提高系统的寻峰精度。
2.2.1 高斯拟合算法
高斯函数与光纤布拉格光栅反射谱基本相同,其表达式为:
(4)
式中:I为反射信号的峰值功率,λs为峰值功率所对应的波长值,Δλ为反射信号的3 dB带宽值。
2.2.2 三次样条插值算法
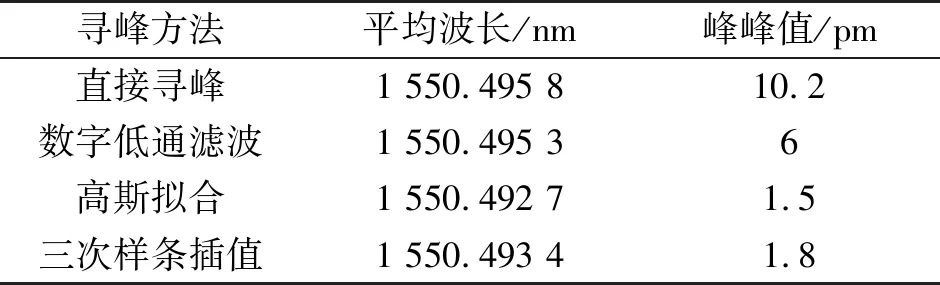
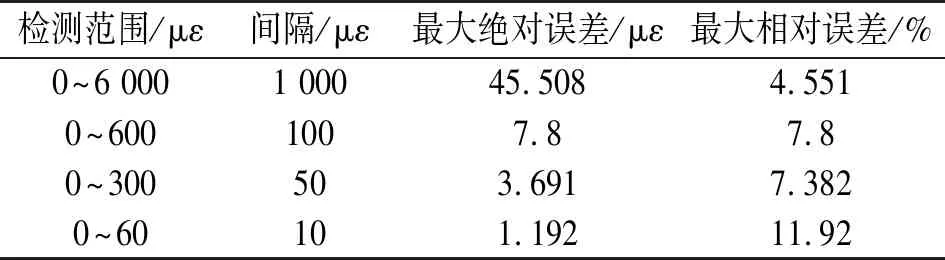
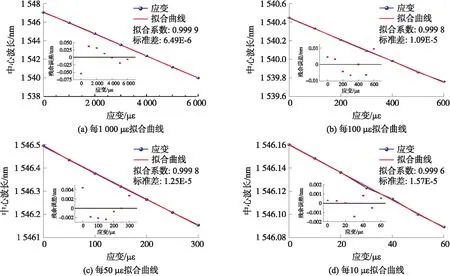
三次样条插值算法具有计算简单、数值稳定性好等优点,在多点插值中具有广泛的应用[12]。设区间[a,b]上有n+1个节点且a=x0 ③s′(x1+0)=s′(xn+0),s″(x1+0)=s″(xn+0) 由于曲线拟合算法是一种动态拟合,需要实时对采集到的数据进行拟合,当运算量较大时,拟合算法会影响解调速度[13]。因此,在满足寻峰精度的条件下,应该选择更加快速的拟合算法。 为了验证数字低通滤波与曲线拟合算法对寻峰精度的影响,使用实验室自行搭建的光纤布拉格光栅解调系统进行实验验证。任意选取一个FBG传感器,将其放置恒温箱中并保持温度恒定,然后解调系统将采集到的数据进行寻峰处理。实验一共15组,首先将数据不经过任何处理直接寻峰并记录其中心波长,然后经过数字低通滤波后再次寻峰并记录其中心波长。数据经过数字低通滤波后,分别进行高斯拟合与三次样条插值,并记录其拟合后的中心波长。 曲线拟合实验结果如图3所示,当反射信号经过数字低通滤波与曲线拟合算法后,寻峰精度依次得到提升。曲线拟合数据见表1,两种曲线拟合算法中心波长的平均值基相差0.7 pm,峰值稳定性在1.8 pm以内。 高斯拟合算法与三次样条插值算法对于提高系统的解调精度基本相同,为了选取更合适的曲线拟合算法,分别对两种拟合算法运算速度进行分析。使用MATLAB对两种算法进行运算并记录其运算时间,其中高斯拟合运算速度为0.96 s,三次样条插值拟合速度为0.26 s。在寻峰精度基本相同的情况下,三次样条插值算法的运算速度为高斯拟合算法的3.69倍。因此,本文选择精度高、运算速度更快的三次样条插值算法作为解调系统的曲线拟合算法。 图3 曲线拟合实验结果 寻峰方法平均波长/nm峰峰值/pm直接寻峰1 550.495 810.2数字低通滤波1 550.495 36高斯拟合1 550.492 71.5三次样条插值1 550.493 41.8 为了验证经过数字低通滤波与三次样条插值算法后解调系统对于应变的解调精度,任意选取一个FBG传感器进行实验测试。将FBG传感器放置在光纤拉伸平台,施加预应力,使FBG传感器处在线性解调范围内。 实验一共分为四组,分别为每1000 με、每100 με、每50 με、每10 με的应变解调,解调结果、拟合曲线及误差分布如图4所示。从图4可得,经过数字低通滤波以及三次样条插值后,解调系统对于应变解调线性度良好,线性拟合系数全部达到0.999以上,最大标准差为1.59E-5。应变解调数据如表2所示,在0~6 000 με的范围内,最大相对误差为4.551%;在每0~60 με的范围内,最大误差为1.192 με。 表2 应变解调数据 图4 应变-中心波长拟合曲线及误差 本文研究了光纤布拉格光栅解调系统中曲线拟合算法优化选取问题,实验分析高斯拟合与三次样条插值算法对于寻峰精度的影响。实验结果表明,两种解调算法对于提高寻峰精度基本相同,三次样条插值运算简单,速度更快,在动态拟合中更有优势。经过数字低通滤波与三次样条插值拟合后,解调系统对于FBG中心波长的稳定性误差小于1.8 pm,对应变解调在0~6 000 με范围内线性拟合系数全部达到0.999以上。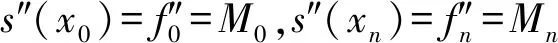
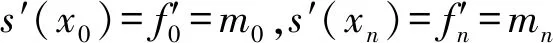
3 解调实验及结果分析
3.1 曲线拟合实验

3.2 应变解调实验
4 结论

