微机械陀螺冲击特性及可靠性研究

何春华,赵前程,杨振川,张大成,闫桂珍

(1.北京大学微电子学研究院微米/纳米加工技术国家级重点实验室,北京 100871)2.美的集团,广东 佛山 528311)

冲击是MEMS可靠性最重要的影响因素之一,与机械振动应力不同,它的加速度幅值非常高、冲击脉宽较小、冲击波形类似于半正弦波或方波脉冲。实际应用环境中,器件可能承受很大的机械冲击力,例如器件从1.5 m的高处跌落到坚固的地面时受到的冲击加速度约为500gn～3 000gn,油气勘探传感器受到的冲击加速度可达20 000gn,炮弹发射过程中器件所受的冲击加速度高达100 000gn[1]。MEMS器件受到较高的机械冲击时,容易发生吸合和粘附失效[2],由于陀螺设有阻挡结构,因此基本可避免吸合和粘附问题。若冲击加速度很大,则陀螺结构在猛烈碰撞时容易产生结构分层或硅渣等微粒污染;当冲击应力大于硅材料的屈服强度时,硅结构(尤其是梳齿或梁)容易发生断裂失效。芬兰阿尔托大学电气工程学院曾对三轴陀螺仪进行冲击试验[3-5],冲击后机械结构的失效模式主要包括梳齿断裂、梁和结构断裂、微粒污染等。此外,在15 000gn高冲击应力下,硅结构及硼硅玻璃结构发生严重形变及裂纹扩展,可见冲击对陀螺影响非常大。

为了更好地分析陀螺的抗冲击能力、以及指导支撑保护结构设计,需对陀螺冲击响应特性进行建模分析。美国麻省理工大学和北京理工大学曾指出固有频率、冲击脉宽、加速度幅值等对MEMS器件的冲击可靠性影响较大,在半正弦加速度冲击下,机械响应特性根据谐振周期T的大小可划分为弹性波响应、谐振响应和准静态响应[6-7],并指出可根据最大的响应位移和应力进行失效判断,但文献中并未给出详细的建模分析和试验验证。纽约州立大学宾汉姆顿大学曾建立了PCB和MEMS结构的二维冲击响应模型[8],但并未给出推导分析和解析解,因此无法根据理论解来分析冲击响应的主要影响因素。尽管国内对悬臂梁做了大量的冲击响应特性建模和研究[9-11],但国内外针对陀螺结构的冲击响应特性建模和试验分析相对较少。综上所述,本文将开展详细的陀螺冲击特性建模研究,从原理上分析影响陀螺结构冲击可靠性的关键因素,并通过实验验证理论分析的正确性。

1 微机械陀螺冲击响应特性分析

假设硅陀螺结构被直接固定在冲击台上,如图1所示,不考虑安装结构、PCB或粘接胶的影响时,则陀螺冲击动力学方程[12-13]为:

(1)

图1 单自由度冲击模型

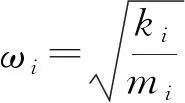
y=y0sin(ω0t)

(2)

式中:ω0为冲击台的激励频率,y0为位移幅值。则冲击加速度为:

(3)

式中:a0为冲击加速度幅值。考虑冲击加速度为半正弦脉冲,如图2所示,则有:

(4)

式中:t0为冲击信号周期的一半,即t0=π/ω0。借用单位阶跃函数u(t)来表示,则上式加速度可统一描述为:

(5)

图2 半正弦冲击波图

对于陀螺结构来说,最重要是考量其相对冲击台的位移而非绝对位移,因此令陀螺运动的相对位移为z=x-y,则式(1)可简化为:

(6)

由于冲击力远大于静电驱动力,因此本文分析将忽略静电力的作用,只针对冲击力进行分析,则上述方程可写成:

(7)

因为硅结构的初始相对位移和速度都为0,则有初始条件:

z(t)=0,z′(t)=0

(8)

由于冲击时间较短,因此冲击响应分析时需同时考虑瞬态响应和稳态响应对陀螺的影响,可求得上述方程的解为:

z(t)=R(t)u(t)+R(t-t0)u(t-t0)

(9)

式中:

(10)

对位移两次求导可得硅结构的加速度a为:

(11)

式中:

(12)

2 冲击仿真分析

根据理论式(9)～式(12)可对位移和加速度响应进行MATLAB仿真,仿真时设置ωi=2π×8 965.5 Hz,mi=7×10-7kg。

①当ω0=ωi,Qi=2 000时,响应加速度随输入加速度峰值a0和时间的变化曲线如图3所示,可见随着输入加速度峰值的增大,响应的加速度也随之增大,响应加速度的峰值约为输入加速度峰值的1.5倍。

图3 当ω0=ωi,Qi=2 000时,响应加速度随输入加速度峰值a0和时间的变化曲线

类似于响应加速度,响应位移也随着输入加速度峰值的增加而增大,如图4所示。当冲击加速度为2 000gn时,位移将达到10 μm,当冲击加速度大于4 000gn时,位移将大于20 μm,事实上梳齿或梁之间的间距一般为10 μm～20 μm,也就是说位移过大时将会发生碰撞。为了防止短路,增加抗冲击能力,结构设计时一般有阻挡结构。因此,若位移过大时,结构将会碰撞在阻挡结构上,若撞击力过大,则结构也会碰坏。

图4 当ω0=ωi,Qi=2 000时,响应位移随输入加速度峰值a0和时间的变化曲线

②当a0=13 000gn,Qi=2 000时,归一化响应加速度(即响应加速度与输入加速度峰值的比值)随ω0/ωi和时间的变化曲线如图5所示,可见当ω0≈ωi时,响应加速度最大,ω0/ωi越小或越大都会导致响应加速度降低。

图5 当Qi=2 000,a0=13 000 gn时,归一化响应加速度随ω0/ωign和时间的变化曲线

类似于响应加速度的分析,当ω0≈ωi时,响应位移最大,ω0/ωi越小或越大都会导致响应位移降低,如图6所示。同样,当响应位移大于20 μm时,梳齿、梁或结构之间将发生碰撞。

图6 当Qi=2 000,a0=13 000 gn时,响应位移随ω0/ωi和时间的变化曲线

③当a0=13 000gn,ω0=ωi时,归一化响应加速度随Qi和时间的变化曲线如图7所示,可见Qi变化几乎不会改变最大响应的峰值,响应加速度的峰值约为输入加速度峰值的1.5倍,但Qi会改变其自由振动的衰减时间,Qi越大响应加速度作用时间越长,累积损伤将越严重。

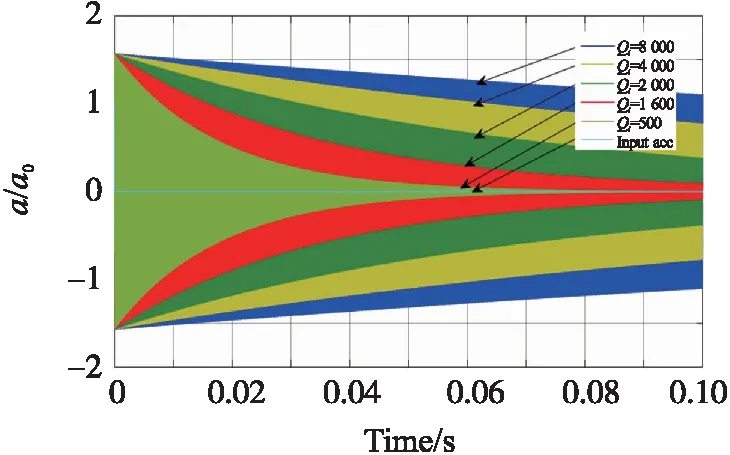
图7 当ω0=ωi,a0=13 000 gn时,归一化响应加速度随Qi和时间的变化曲线

类似于响应加速度的分析,Qi变化也几乎不改变响应位移的峰值,但会改变其自由振动的衰减时间,衰减时间与Qi成正比,Qi越大响应振动时间越长,累积损伤将越严重,如图8所示。同样,当响应位移大于20 μm时,梳齿、梁或结构之间将发生碰撞,更容易导致断裂失效。

图8 当ω0=ωi,a0=13 000gn时,响应位移随Qi和时间的变化曲线

综上所述,影响陀螺冲击特性的主要因素有冲击加速度峰值和脉宽、陀螺固有频率和品质因子等;当脉宽对应的冲击频率与陀螺固有频率越接近,并且陀螺品质因子和冲击加速度幅值越大时,则陀螺结构的响应位移和加速度就越大,冲击损伤越严重,陀螺越容易发生断裂失效。

考虑最坏情况,则有效冲击力Feff_ma峰值为:

Feff_max=miamax≈3mia0/2

(13)

考虑到质量块mi由4根弹性梁支撑,而所设计的陀螺弹簧梁为U型折叠梁,如图9所示,其每一段长度为L,厚度为h,宽度为w1,b为端梁长度,w2为端梁宽度,通常w1=w2,L≫b,则根据能量法可求得梁在x和y方向的刚度为:

(14)

(15)

图9 U型折叠梁结构图

(16)

(17)

3 冲击试验方案

考虑到陀螺的冲击响应与冲击加速度峰值、脉宽、品质因子和固有频率相关,并非脉宽越大响应越大。前面理论分析表明当脉宽对应的冲击频率与陀螺固有频率越接近,并且陀螺品质因子和冲击加速度幅值越大时,则冲击损伤越严重。因此本文将考虑最严酷的情况,针对固有频率和品质因子设计不同的冲击试验方案,以验证理论分析的正确性。

图10 落锤冲击试验台,陀螺表头用502胶水粘接在冲击台面上

考虑到落锤冲击试验台基本能满足所有的冲击试验,因此本文主要采用落锤冲击试验台来进行冲击试验,部分冲击试验采用马希特锤来完成,如图10和图11所示。特别说明:由于试验设备原因,冲击加速度峰值和脉宽的设定值和实际值可能存在一定的偏差,但一般偏差较小。考虑到试验时间和成本,每一种冲击试验条件对应的样品数为1个～2个,由于冲击前先进行中测(扫频及噪声测试)筛选,因此可有效保证每个待测样品均正常完好。此外,为避免累积损伤的影响,每个陀螺只允许进行一次冲击试验,这样可保证试验结果具有代表性。

图11 马希特锤冲击试验台

4 冲击试验分析

下面以x轴的冲击试验为例进行说明,y轴和z轴的试验分析也类似。MEMS陀螺x轴的固有频率ωi约为8.9 kHz,其对应的周期Ti约112 μs。其他部分关键参数为:mi=0.7×10-6kg,L=400 μm,h=80 μm,w1=14 μm。

4.1 变幅度冲击测试

真空封装陀螺样品的品质因子约为Qi=2 000时,考虑最坏情况,冲击试验台的脉宽设置为Ti的一半,即56 μs。冲击加速度峰值分别设置为10 000gn、12 000gn和14 000gn,每次冲击试验前后分别对陀螺进行扫频试验,一旦发现扫频曲线异常,则判定结构失效,此时应进行开封分析,并用显微镜进行结构的内部目检。

图12 14 000 gn冲击试验前后微梁的金相显微图

冲击试验结果如表1所示,硅微梁的屈服强度σsi为7 GPa,根据式(17)可算得σbm_max的大小。对于弹簧梁,因为5.52 GPa接近屈服强度,并且Qi较大,长时间作用的冲击力带来的累积损伤使梁发生断裂失效,可见试验结果和理论分析结果基本一致。14 000gn冲击试验前后微梁的金相显微照片如图12所示,可见冲击加速度峰值越大,越容易发生断裂,而梁的端部是应力集中点,因此断裂在此处发生。若输入的冲击加速度峰值设置为20 000gn,则可算得σbm_max为7.88 GPa,大于屈服强度σsi,此时尽管降低品质因子,梁也会快速发生断裂失效。

表1 不同冲击加速度幅值的试验结果

4.2 变阻尼冲击测试

冲击加速度峰值设置为13 000gn,考虑最坏情况,冲击试验台的脉宽设为Ti的一半,即56 μs。3个真空封装陀螺样品的品质因子Qi分别为500、1 000和2 000。

冲击试验结果如表2所示,梁的最大应力接近屈服强度,但若外应力作用时间较短,则梁只会发生裂纹扩展,只有损伤累积到一定程度才会发生断裂失效。由于Qi为500或1 000时,自由振动衰减时间较短,即冲击力作用时间较短,不足以发生断裂失效,而当Qi为2 000时,累积损伤较大,最终发生断裂失效,结合上述两个表的试验数据可知13 000gn为临界断裂加速度。Qi=2000时冲击试验前后微梁的金相显微照片如图13所示,可见品质因子越大,累积损伤越严重,越容易发生断裂失效。

表2 不同气体阻尼陀螺样品的冲击试验结果

图13 Qi=2 000时冲击试验前后微梁的金相显微图

4.3 变脉宽冲击测试

冲击加速度峰值设置为13 000gn,陀螺样品的品质因子Qi为2 000,冲击试验台的脉宽分别设为20 μs、56 μs和200 μs,对应的冲击频率ω0分别为25 kHz、8.9 kHz和2.5 kHz。

冲击试验结果如表3所示。结合式(9)～式(17)、可算出最大峰值加速度amax和σbm_max。对于梁,因为5.12 GPa接近屈服强度,在长时间应力作用下,较大的累积损伤会导致梁发生断裂失效;而其他脉宽对应的σbm_max均小于σsi的一半,梁只发生轻微损伤、无断裂失效,可见试验结果和理论分析结果基本一致。脉宽为56 μs时冲击试验前后微梁的金相显微照片如图14所示,可见冲击脉宽对应的频率越接近陀螺的固有频率ωi,冲击响应越大,共振容易导致断裂失效,而梁的端部是应力集中点。

表3 不同脉宽的冲击试验结果

图14 脉宽为56 μs时冲击试验前后微梁的金相显微图

综上所述,理论分析和试验结果基本一致。

5 结束语

本文详细推导了微机械陀螺的冲击响应特性,并进行了MATLAB仿真分析。冲击试验结果表明,理论分析和试验结果基本一致,当脉宽对应的冲击频率与陀螺固有频率越接近,并且陀螺品质因子和冲击加速度幅值越大时,则冲击带来的影响就越大,梁越容易发生断裂失效。因此要使得陀螺具有较强的抗冲击能力,必须综合优化设计陀螺的真空度和固有频率。