基于比值测量法优化磁通量传感器性能的实验研究*

任 亮,姚雪佳,修成竹,冯唐政

(大连理工大学海岸与近海工程国家重点实验室,辽宁 大连 116023)

铁磁材料在民用建筑以及大跨结构中应用甚广,在结构的正常使用期间,有必要使用结构健康监测系统监测测量杆件张力[1-3]。目前传统钢缆索索力测量方法,如液压法、光纤光栅法、振动频率法、压力传感器测定法、应变片测定法等[4-6],都存在明显缺陷,在工程中的应用范围很受限制。基于铁磁材料磁弹效应的磁通量传感器,作为一种新型传感器,能够实现无损地测量桥索、预应力结构的体外索和预应力筋等构件的张力测量[2,7]。由于其耐腐蚀性好、张力测量精度高、过载保护能力强、寿命长等优点[8-9],在工程中得到了广泛应用。

现有的磁通量传感器通常用感应电压积分值来评估缆索内张力大小。然而,由于信号通道的差异或者外部接线电阻的变化会影响励磁电流的大小,从而影响索力测量结果,降低了传感器测量灵敏度。

文中提出了一种利用创新性的比值测量方法监测索力的磁通量传感器。建立了励磁系统的的电感—电阻(LR)模型,证实了仪器信道的差异或外部接线电阻会影响励磁电流,从而会导致感应电压的不准确。在此基础上,建立了传感器系统的变压器理论模型,以获得比值结果和外部索力的显式关系。同时进行了相关实验研究,探讨了感应电压法和比值测量法的传感器性能。

1 理论模型

1.1 磁通量传感器测量原理

铁磁性材料在外磁场作用下会被强烈磁化,磁导率很高[4,10]。所以即使在弱磁场作用下,铁磁性材料也能得到很大的磁化强度[1]。当铁磁性材料受到外力作用产生机械应力或应变时,磁化强度就会发生改变,即磁弹效应[5,9]。磁导率是铁磁性材料的一个重要参数,表示为:

μ=B/H

(1)

式中:B是磁通量密度,H是磁场强度,μ是磁性材料的磁导率,依赖于H。

磁通量传感器由一个初级线圈和一个次级线圈缠绕在被测铁磁构件上组成[7,10-11]。当交流或脉冲电流信号通过初级线圈时,就会产生一个随时间变化的磁场,根据法拉第电磁感应定律,在次级线圈中会产生感生电动势[6,12-14],其值与线圈内磁通量随时间变化率成正比,表示为:

(2)

式中:εout为感应电压,N为线圈匝数,φ为磁通量,μ0为真空磁导率,Ab和Ac分别是次级线圈和试件的横截面积。

在激励线圈的磁场下,被测试件存在和不存在时,次级线圈的感应电压的积分值分别表示为:

(3)

V0=NAbμ0ΔH

(4)

式中:Vc和V0分别是有试件和没有试件时的次级线圈感应电压积分值。通过式(3)和式(4)可以得到相对磁导率μr为:

(5)

因为Ab、Ac和V0都是常数,Vc是唯一变量,所以,方程(5)说明次级线圈产生感应电压的积分值与磁导率线性相关。

1.2 励磁电路的LR模型

选择带一组频率分量的脉冲信号作为激励信号,应用于初级线圈。由于脉冲信号在低频范围内,线圈电容可以忽略不计,因此,励磁系统可以通过LR电路建立模型,如图1所示。

图1 励磁系统LR模型

励磁系统的一阶线性微分方程为:

(6)

式中:L1为初级线圈电感,R为导线电阻r0和线圈电阻r1之和,i1为激励电流,Us为激励电压。通过方程(6),解得通过激励线圈的电流i1、电感电压Ui和激励线圈两端电压Uc可以表示为:

(7)

(8)

式中:A为激励电压幅值,当脉冲励磁电压通过传感器线圈时,由于线圈的电感,励磁电压上升或下降沿的励磁电流发生变化,从而产生线圈电压,感应电压随之变化。

1.3 传感器系统变压器模型

图2所示传感器系统的变压器模型给出了电磁传感器的工作原理。当在激励线圈两端输入一个变化的信号时,根据法拉第定律,感应线圈会产生感生电动势,感应线圈的感应信号与激励信号相反。

图2 传感器系统变压器模型

根据基尔霍夫电压定律(KVL)和法拉第电磁感应定律(FEIL),可以得出:

(9)

式中:U1为线圈激励电压,U2为感应电压,N1和N2分别为激励线圈和感应线圈的匝数,φ1和φ2为激励线圈和感应线圈的磁通量,由于试件的磁导率高于非磁性线圈骨架的磁导率,所以可以忽略不计。

根据式(7)～(9),感应电压积分值与激励电流变化的比值可以表示为:

(10)

式中:k1为耦合系数,Ac为试件截面面积,l为线圈长度,μ0为真空磁导率,μr为相对磁导率。

在索力测量中,由于采集器通道的差异或外部导线电阻的变化,可能会导致励磁电流的变化,从而影响传统磁通量传感器采用感应电压法的张力测量结果。因此,本文提出了比值测量方法,消除了励磁电流对测量结果的影响,有利于提高传感器的性能。

2 实验装置

2.1 传感器系统结构

缆索张力监测由传感器系统实现,如图3所示,主要包括三个部分:电磁传感器、信号采集仪、LabVIEW监控模块。利用EM传感器测量了试样上张力作用引起的磁场变化。所研制的信号采集仪不仅能产生合适的激励信号通过初级线圈对试验试件进行磁化,而且能接收到穿过次级线圈的感应信号。

图3 传感器系统结构示意图

2.2 两种测量方法比较

通过由激励模型、增益放大器、低通滤波器和积分电路组成的8通道数据采集系统对传感器信号进行激发和采集。由于外接信号线长度或种类的差异,其电阻值会有差异,进而影响到激励电流值,最终影响感应电压积分值。采用六根电阻值不同的信号线,分别进行4次初值采集,分别采集感应电压结果与比值结果。为比较两种测量方法下传感器的性能,提出相对变化率概念,计算公式为:

(11)

式中:S为相对变化率,Ri和Ri-1分别为第i次和第i-1次外接信号线电阻,Yi和Yi-1分别为传感器对应的输出。由两种测量方法的平均结果计算出的六种信号线的统计结果如表1所示。

由表1结果可知,比值测量结果的标准差小于感应电压结果,由于感应电压结果(mV)和比值测量结果(mV/mA)的量纲不同,选择变异系数而不是标准差作为比较参数。结果表明,两种测量方法的变异系数远小于1%,说明在此条件下两种测量方法都能满足工程精度要求。此外,在六种不同外接信号线条件下的初值测量中,所提出的比值测量方法的相对变化率小或等于传统的感应电压法,如图4所示,表明所提出的比值测量方法提高了传感器的性能,能更好地解决由于信号线不同带来的初值漂移问题。

表1 两种测量方法中6种信号线的测量统计结果

图4 两种测量方法相对变化率的比较

2.3 拉力实验

图5 加—卸载实验装置图

本次实验为单轴拉伸实验,实验所用杆件为内径10 mm,外径20 mm的空心圆杆,材料为45号钢材。在杆件上安装磁通量传感器,通过信号线接入采集仪,利用LABVIEW模块进行采集感应电压积分与比值结果。通过SANS试验机对杆件进行拉伸加—卸载,如图5示。为减小实验误差,做三次重复实验,并对实验结果平均值进行分析。如图6示,两种方法的三次实验结果重复性良好,且加—卸载结果具有良好的一致性,除此之外,很明显地,感应电压积分值和比值结果都随拉力增大而下降。

图6 两种测量方法的实验结果

为比较两种测量方法下的传感器性能,分别使用线性拟合度、相对灵敏度做比较,其中相对灵敏度通过以下公式计算,表示为:

(12)

式中:Z为相对灵敏度,F(t0)和F(t)为初始条件和某一阶段的张力,Y(t0)和Y(t)为传感器对应的输出。在相同实验条件下,比较两种测量结果的线性拟合度,如图7和表2所示。

由表2结果分析可得,比值测量方法与感应电压测量方法下的传感器的线性拟合度差值很小,且传感器测量结果线性拟合度均大于0.99,可以满足工程要求。

为比较二者相对灵敏度,取加载段0～10 kN每1 kN结果求相对灵敏度,初始状态为0 kN,结果如表3示。

图7 两种测量方法实验结果

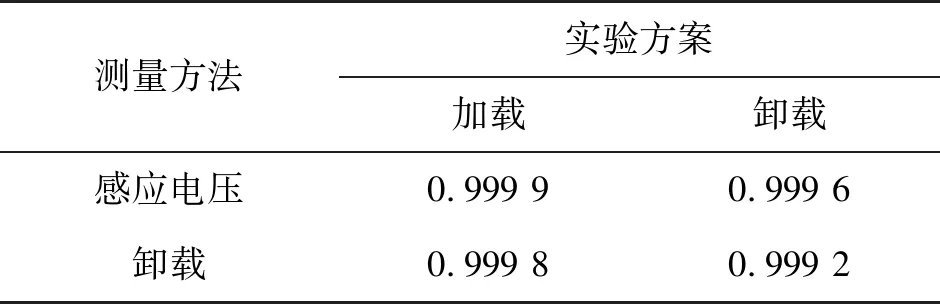
表2 两种测量方法加—卸载实验结果线性拟合度对比

由表3可知,虽相对灵敏度随力值有所波动,但误差均在2%以内,满足工程要求。把两种测量方法下的相对灵敏度作图,如图8所示。

通过图8可以很明显的地看出比值测量方法结果的相对灵敏度高于感应电压法的结果。通过计算平均值,比值测量法的平均相对灵敏度为1.56%/kN,相较于感应电压法的平均相对灵敏度1.22%/kN提高了27.85%。同样地,通过对卸载段结果分析,也有类似结论。

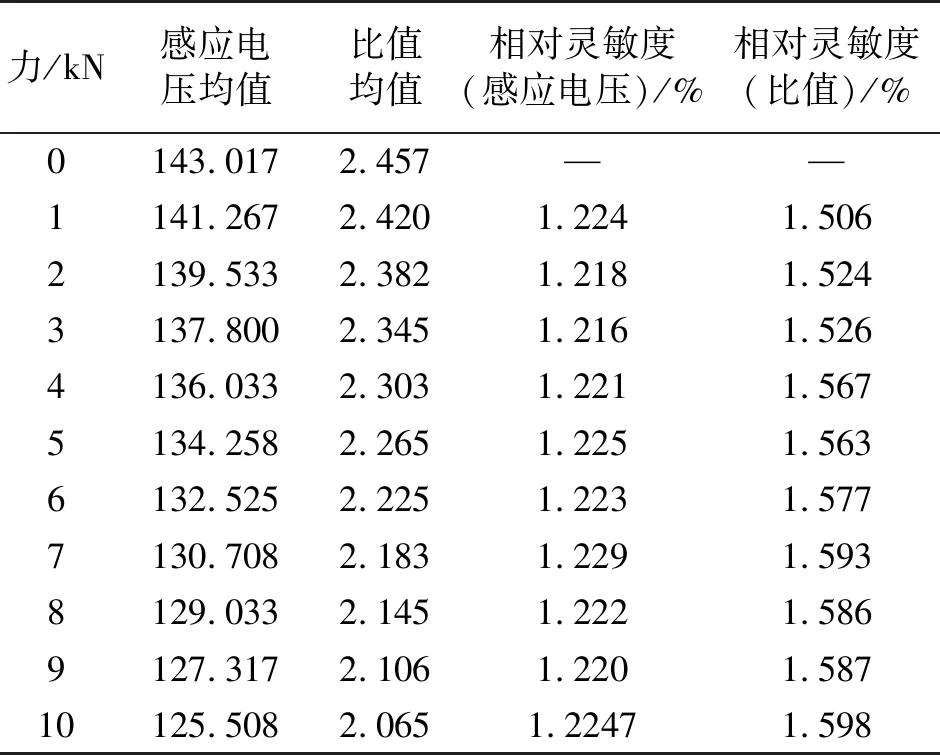
表3 两种测量方法相对灵敏度的测量统计结果

图8 两种测量方法结果的相对灵敏度对比

3 结论

将一种创新性的比值测量方法用于监测缆索张力的磁通量传感器。提出励磁系统的LR模型,说明了外部导线电阻的变化会影响励磁电流,进而导致感应电压的不准确变化。建立了传感器系统的变压器模型,得到了比值结果与外张力的显式关系。实验接入六种不同电阻的外接信号线,通过对测量结果分析,证实了外部导线电阻的变化会影响感应电压积分值,进而导致力结果的不准确性,使用比值法来测量,可以有效避免外接信号线电阻的变化带来的不良影响,解决这种情况下的初值漂移问题。

通过分析拉杆单轴拉伸实验结果,证实了比值随外张力的变化与传统的感应电压法一样,呈线性相关,且线性拟合度高于工程要求。这表明,比值结果与外张力呈线性关系,与理论推导结果吻合较好,该方法能够较好地实现缆索等铁磁构件的张力测量。且利用比值测量方法,将传感器的相对灵敏度从1.22%/kN提高到1.56%/kN,提高了27.85%。