构造函数，巧解含参不等式

江苏省射阳县陈洋中学 黄晓丽

构造函数法在含参不等式中应用得十分广泛，就是利用转化的思想，通过构造函数将含参不等式进行转化，然后充分利用函数的性质去解决含参不等式问题。所以，学生要清楚地知道构造函数的方法也是解决含参不等式的一种方法，教师在实际教学过程中要不断地灌输，日积月累，学生的成绩就会有质的飞跃。

一、构造函数——分离参数

学生在求解含参不等式问题时，有时候进行分类讨论反而会显得十分复杂，这时候，学生可以学会将含有参数的式子进行合理的变形，把含参不等式中的参数分离出来，将含参不等式表示成一端只包含参数的式子，另一端则是转换成与参数不等式没有关系的式子，然后利用构造函数的方法，用函数的单调性与性质去讨论原不等式的解集的情况。

分析：不等式的两边只有一个a，所以就比较容易想到运用“分离参数”法，将参数a 分离出来，将含有x 的放在一边，根据定义域，列出一边只有a，一边只有x 的不等式，构造函数，用函数的性质求函数的最小值，根据函数的最小值求出实数a 的取值范围。

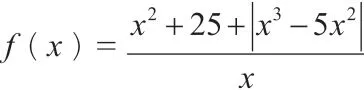
评注：本题中，学生仔细观察题目中给的式子，就会发现本题的参数是a，因此思路由此打开，将参数a 与自变量x 分离出来，带有自变量x 的放到一边构造出函数，回归到学生熟悉的求解函数最值的形式，提升了解题的效率。

二、构造函数——变更主元

所谓“变换主元”法，就是在求解含参不等式问题时，选取其中的一个字母作为主元，将其他的字母看作常数，然后构造出函数，通过利用函数的特点与性质，求出函数的最值，最后再返回到含参不等式中，正确地求解含参不等式的范围。

例2 对于满足0 ≤p ≤4 的一切实数，不等式x2+px＞4x+p-3恒成立，试求x 的取值范围。

分析：欲求x 的取值范围，在满足定义域的情况下，学生就可以将字母p作为自变量，x作为参数，利用“变更主元”的方法构造出函数，将含参不等式问题转化成函数问题，利用函数的性质正确地求解。

解：根据题意，由x2+px＞4x+p-3 可得，p（x-1）+x2-4x＞0，令f（p）p（x-1）+x2-4x+3，p ∈[0,4]。此时f（p）为一次函数，若f（p）＞0 在p ∈[0,4]上恒成立，那么只要f（0）＞0，f（4）＞0，综合以上所述，x 的取值范围为（-∞，1）∪（3，+∞）。

评注：此题学生要注意的就是在变更主元构造函数的过程中，主元不要过于复杂，要已知主元的定义域，不然学生构造的主元就没有意义了。

三、构造函数——还原导数

导数、函数以及含参不等式这三者之间存在密切的联系，学生在求解含参不等式的过程中，导数还原也不失为一种方法，其操作过程就是还原导数，然后构造出函数，再利用函数的性质求解。

例3 设函数f'（x）是奇函数f（x）（x ∈R）的导函数，f（-1）=0。当x＞0 时，f'（x）-f（x）＜0，试求使得f（x）＞0 成立的x 的取值范围。

分析：根据题意，学生可以知道f'（x）是f（x）的导函数，那么在已知条件的基础上，当x＞0 时，f'（x）-f（x）＜0，学生可以联想到的导函数为，然后构造出函数，正确求解。

评注：学生在求解的过程中，如果看到题中有导函数，就可以思考是否有和某个函数的导函数相似的地方，这或许就是解题的关键所在。因此，学生在解题的过程要足够细心，不遗漏一个条件，方能找到切入点打开思维。

总之，构造函数的方法是解决含参不等式问题的一大法宝。不等式问题与函数有着密切的联系，就像方程与函数的联系一样，学生要想掌握构造函数的这几种方法，就需要不断地练习，找寻到问题的关键所在，才能解决根本的问题，才能突破自己，收获事半功倍的效果。