小学数学课融合数形结合思想开展教学之尝试

安徽省合肥经开实验学校 冷利娟

数形结合思想方法在数学教学方面占据重要地位，主要是通过数形之间的相互转化与利用来对数学问题进行解决，是抽象数学语言和直观图形有效结合的体现，也是抽象思维和形象思维相结合的体现。

一、渗透数形结合思想，增强数学概念的理解

数学概念实际上是人的大脑对现实生活中某一对象的数量关系及空间形式相关本质特征的一种反映，也可以被称为数学思维形式，其抽象性与逻辑性都比较强。而在数学概念的教学中渗透数形结合思想，可以让学生对图形中蕴含的数形关系进行分析，然后直观地理解相应的数学概念。比如在苏教版小学数学三年级“认识分数”这部分的教学中，教师先引导学生初步认识某个整数的几分之一，即把某个事物看作一个整体，将其平均分成几个部分，每个部分都相当于这一整体的几分之一。为了让学生有效认识分数，教师可渗透数形结合思想方法。比如教师将12 根小木棒看作一个整体，将其分成12 份之后，每根小木棒都相当于这个整体的。这时教师可以向学生提出问题：“若是这些小木棒可以代表的分数有等等，那你是否可以将其位置生动地表达出来？”在这样的数学问题中，数轴类的图形可以有效表达相应的位置关系，将抽象的分数知识转化成为简单易懂的数学内容，如图1 所示：

图1

图1 所表示的分数位置有效地体现了分数之间的大小关系，还能让学生直观地理解每个分数所代表的含义，使学生深刻认识分数这一概念。这是数形结合思想在小学数学概念教学过程中得以有效渗透的体现，克服了数学概念课程教学低效化的问题，提高了学生对数学概念的学习效果。

二、渗透数形结合思想，准确把握数学本质

数学的抽象性及逻辑性是固有的学科特点，但是教师却可采用有效的教学策略来将抽象的数学知识转变成为直观可感的数学内容。其中，数形结合思想的渗透就可以实现这一教学目的，将其应用在学生的数学学习中，能有效激活学生的数学思维，并将数学的本质更清晰地呈现在学生面前，使其准确把握数学知识中蕴含的数学本质。华罗庚很明确地指出：在数缺形的情况下，直观性不强；在形缺数的情况下，则很难观察入微，难以体现其数学本质。因此，数学教师要提高数学课堂教学效果，就需要渗透数形结合思想，让抽象又复杂枯燥的数学知识可以转化成为直观又简单生动的数学内容，促使学生的抽象思维与形象思维获得协调性的良好发展。

比如在苏教版小学数学四年级“运算律”的教学中，教师就可依托教材来改进练习题目，如：“在同一块菜地中，将其分成两个区域，分别栽种白菜和菠菜。其中栽种白菜的区域为长与宽分别是25m、6m 的长方形，而栽种菠菜的区域则是长与宽分别为15m 和6m 的长方形，那么请问它们的面积总共是多少？”有的学生在解答时将它们合并成为一个大的长方形来进行计算，也有的学生是分别计算两个长方形面积之后，将两者的面积结果相加。为了理清其中的数形关系，教师可引导学生绘制出相应的图形。

三、渗透数形结合思想，培养学生的逻辑推理能力

培养学生的逻辑推理能力是数学课程标准对教师提出的重要教学要求，可以帮助学生更好地掌握数学知识之间存在的内在联系，以有效理解抽象的内在逻辑关系。尤其是在公式推导方面，教师可以有效锻炼学生的逻辑推理能力。而数形结合思想方法的渗透可以辅助教师达到培养学生逻辑推理能力的教学目标，教师可积极将其渗透在公式推导类的教学过程中。比如在苏教版小学数学五年级《三角形面积的计算》这一课的教学中，教师要让学生合理推导出三角形面积公式，并加强其对这一面积计算公式的理解，可采取数形结合的方法来进行教学。教师在教学过程中，可为学生呈现图2 的几个三角形几何图，让学生观察其中的数形关系，并推导三角形面积的计算公式。

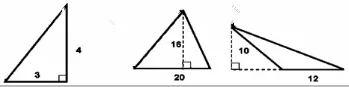
图2

在公式推导的过程中，为了更好地体现出图2 中数形之间的本质，可绘图，如图3 所示：

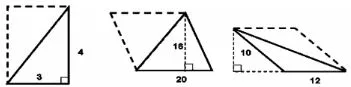
图3

在求解第一个三角形的面积时，据图可知底和高分别是3 和4，可将其面积计算公式列为：3×4÷2=6。由于原有直角三角形的斜边与虚线构成的三角形和该直角三角形完全相同，共同构成了一个长方形，则3×4 代表的是这一长方形的面积。而在求解原有直角三角形面积时需要除以2，主要是因为这一三角形的面积就是该长方形面积的，这也就推导出了直角三角形的面积计算公式。其中，S 代表的是三角形的面积，而a 和b 分别代表三角形的底和高。通过同样的公式推导方式，可以继而推导出图3 中另外两个三角形的面积公式。在这一公式推导过程中，学生可以更容易地理解三角形面积计算公式和图形之间的关系，同时学生也更清晰地了解到三角形面积和拼成的四边形面积之间的内在联系，深刻理解了公式中“”的含义，利于学生有效记忆和巩固三角形面积计算的数学知识。

综上所述，数形结合思想应用在小学数学教学中具有重要的教学价值，小学数学教师应该注重渗透这一思想方法，展开有效的课堂教学活动，促使学生在数形结合思想的指引下有效理解抽象的数学知识内容，直观地获取一些数量关系，可提高学生在数学学习中的解题效率。