积累基本活动经验目标下的“变化的量”教学策略

江苏省盐城市毓龙路实验学校 徐 明

在《比例》设计教学时，将知识目标中引入数学思考，搜罗能展现基本活动经验的学习素材，激活学生观察图形、分析数据、动态读图的经验，帮助学生启动沟通前后知识、联结两个相关变量构成比例的思维活动程序，进行数学推理。

一、图片拖动中的比例关系

（板书课题，先写“形状”，然后前置“不变的”三字）

师：举例说明什么是比例？

学生列举商品数量和总价、时间和路程、工作效率和工作总量等。

师：今天我们就来研究“比例”，看看能不能刷新你的原有认识。

师：（呈示课本33 面第1 题，如下图）先审题，然后小组合作讨论。

学生先个别思考，再组内交换意见，集中汇报展示。

生：上题中长方形图案的长度和宽度都在变。（教师板书“长度、宽度”）

教师用软件动态演示拖拽图形长度，缓慢延长的过程，将相关数据列表。

长度（厘米） 8 16 24 32 40 12 12.8 20宽度（厘米） 5 10 15 20 25 7.5 8 12.5

生：我发现每次拖动长度延长8 厘米后，宽度会自动延长5 厘米，增幅稳定。

生：（表示反对）但是到后来长度的增幅不是8 厘米，宽度也不再是每次延长5 厘米，甚至到后来都不是整厘米数。

师：对，我们考虑问题要周全，慎重。不能妄下断言。

师：再次仔细观察表格中的数据，概括一下两组数据的关系？

生：宽度随着长度一起延长。

生：长度延长的同时，宽度也在延长。

师：根据大家观察的结果，我们发现宽度会随着长度的延长而延长。 一个量的变化会引起带动另一个量的变化，这是一种新的动态数量关系。

【思考】应让学生初步意识到本次研究的重点是数据的动态变化关系，是宏观的、整体的，不是局部片段的，学会用联通发展的眼光审视分析数据，特别应学会全面、缜密地分析事物。

二、探究形状不变与比例的关系

师：审读课本第2 题（如下图）。思考：该如何放大，才能保证矩形的长、宽都扩大相同倍数？缩小呢？

生：按照比例规定，计算出长度和宽度按此比例变化后的长度。

师：试着计算出长度和宽度按照规定比例变化后的占格情况。

生：长度占格变多的同时，宽度占格也变多。

师：仔细观察图形，还能发现什么？

生：无论怎么放大和缩小，长方形的基本形状没有变。

师：没错，这就是说长方形的长宽尺寸比例决定了长方形的基本形状，在按一定比例扩大或者缩放的过程中，长方形的长宽尺寸比始终不变，那么，长方形在按比例变化后，哪些量变了？哪些量没变？

生：面积大小和周长都变了，只有形状（长宽比）没有变。

师：回顾第1 题和第2 题，都涉及两个“比例”，它们有什么差异？

生：第1 题，随着拖拽延伸长度，宽度随之延长，而第2 题中则要同时延长长度和宽度。

师：无论怎么说，确定比例就是要维持两个量的相对倍率关系稳定。

【思考】首次试教，问学生读懂了什么？哪里搞不懂？分析太细致，涉及面太广，无法触及比例的核质。二次执教弱化了数格子数，直接观察形状看比例。对于第（1）题，只关注数量变化规律，一语带过。后两题需要学生综合两个量的同步变化，作出研判。链接到第1 题，前后照应。

三、用比值恒定来揭示比例的定义

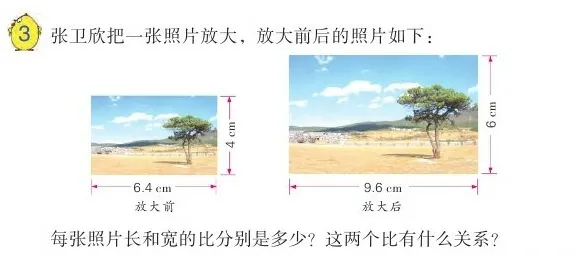
师：研读课本第3 题（如下图），做好读书笔记。

学生答题，将算出的比值汇报展示。

师：这里的前后两张图片有什么关系？对于长和宽，怎么控制它们的相对关系？

生：赋予长不同的数值。

生：长等于6.4 时，宽等于4；长等于9.6 时，宽等于6……长取值不同，宽对应的数值也会变化。

生：长与宽相除的得数1.6 是比值，长与宽的数值一一对应。

师：研究了三道题，用一句话总结，怎么说？

生：比值一定的几个比之间构成比例关系。

师：这种比例关系在生活中普遍存在。它们可用图表、分式、比例式来表示。

【思考】教学此题时，我删去了首次试教时用图表数据表达和分数表达这一环节，因为此环节无益于达成教学目标，教学时就应有所取舍。

通过试教和反思，我深刻意识到这节预热课不仅能够帮学生积累“比例”的操作经验，更能积累思维经验，思维经验也是基本活动经验的有机组成部分。教学节奏虽然变慢，但是学生的基础更扎实。