租船问题研究
广东省广州市天府路小学 陈欣言
在义务教育教科书数学四年级下册第一单元《四则运算》的例5(课本第10 页),主题是租船问题:游客有32 人,大船30 元每艘,可载6 人,小船24 元每艘,可载4 人,问怎么租船租金最少?课本上的策略是通过计算和比较得出结论:先尽量租人均价格便宜的船,再考虑不留空位,就会最省钱,这样得到的方案是大船4 艘,小船2 艘。
经过思考,我想到不通过计算,画图也可以得出最便宜的方案。○表示一艘大船的价格,△表示一艘小船的价格,显然有:○>△。全部租大船:32÷6=5(艘)……2(人),至多需要大船5+1=6(艘),用6 个○表示;5 艘大船和1 艘小船用5 个○、1 △个表示,下面类同,所有的方案表示如图1:
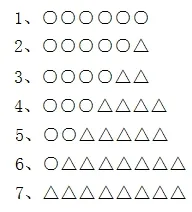
图1
怎么比较它们的成本呢?我采用分组比较的方法,如图2:

图2
在每组中扣除相同的部分,又已知小船便宜,显然,第一组中3便宜;第二组中5 便宜;第三组中7 便宜。因此只要比较3、5、7。
先比较5 和7:
我再想了一下,如果把题目的条件改一下变成“游客有33 人”会怎样呢?显然不可能没有空位,因为游客是奇数,大小船载客都是偶数,那应该怎么办呢?这样一来,最省钱的方案应该是5 艘大船和1 艘小船(比4 艘大船和3 艘小船便宜)。为了研究一下这个结论是否正确,我继续使用画图列表法,把所有可行方案都列出来,如图3:
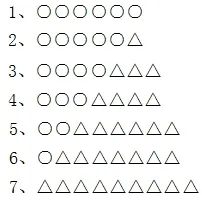
图3
同样进行分组比较(如图4 所示):第一组中2 便宜;第二组中4 便宜;第三组中6 便宜。再比较2、4、6、7,显然2 比4 便宜,4比6 便宜,6 比7 便宜,所以,最便宜的方案就是5 艘大船和1 艘小船。

图4
每一组去掉相同部分,可知第一组中2 便宜;第二组中4 便宜;第三组中6 便宜。再比较2、4、6、7,也可以得知:2 比4 便宜,4比6 便宜,6 比7 便宜,所以,最便宜的方案就是5 艘大船和1 艘小船。
接着,我又把课本题目的条件改了一下,游客还是32 人,但是小船的价格改为48 元,大船不变,这样的话全部租大船反而是最便宜的了(虽然大船上留有空位),原来没有空位的4 条大船和2 条小船反而不是最便宜的了。
看来,这种题目还是需要画图列表法才能筛选出最省钱的方案!但画图列表法本质上是穷举,如果题目的数字很大就要花很多时间了。我研究了几天,找到了一种改进的方法,我把它叫作“凑整替换法”。如课本上的题目条件不变,先考虑全部使用贵的小船,此时需要8 艘,然后把小船分组拼团,一组内小船的数量需要满足能完整(不留空位)的用大船替换的条件(本质上是求大船载客数和小船载客数的最小公倍数),如题大船载客6 人,小船载客4 人,一个分组内的载客数就是12 人,此时需小船3 艘,能被2 艘大船完整替换。替换之后每组的成本肯定是降到最低的,只需要对最后余下来的人数进行列表法穷举就行了,如图5 所示:

图5
对余下的2 艘小船(8 人)进行画图列表法穷举,如图6:

图6
显然,1是最便宜的方案。如果小船价格改为48元,就是3最便宜。如果人数改为33 人,价格不变,余下就是3 艘小船共9 人,这时2最省钱,也就是图3 条件下得到5 艘大船和1 艘小船的方案。
一道简单的数学课本题目,改动一个数据,参考量影响因子也会变化,所以对方法要理解到位,不能生搬硬套方法和结论。另外,一种分析策略也可以通过不断优化,实现更简洁的解题方法和思考过程。

