波形钢腹板组合梁挠度计算方法对比
叶华文,胡劼成,史占崇,徐勋,王力武
(西南交通大学 土木工程学院,四川 成都 610031)
波形钢腹板组合结构自重轻、受力明确,可以有效降低混凝土的预应力损失。自20世纪80年代起,波形钢腹板新型组合桥梁在法国、日本、中国等国家得到了广泛的应用与发展。这种组合结构的波形钢腹板较薄,其褶皱效应明显,导致抗剪刚度较小[1-2],因此需要考虑钢腹板引起的剪切挠度。

以上波形钢腹板组合梁挠度计算方法可总结为5种 方法,即经典梁法、Timoshenko梁法、弹性剪切变形法、有效刚度法和三角级数理论。有限元模拟成本较低,在合理的边界条件下结果较为准确,因此本文在对比分析各种方法的基础上,通过有限元模拟讨论不同方法的理论差异及适用条件。
1 挠度计算方法
选取典型波形钢腹板组合梁结构体系(简支梁和悬臂梁),简支梁分析模型如图1所示,悬臂梁模型类似,在此不列出。图中:P为集中荷载;c为竖向荷载到左侧支座的水平距离;L为组合梁跨度;H为组合梁高;h0为钢腹板高;α为钢腹板转角;φ为上下混凝土板的转角。

图1 简支梁分析模型
波形钢腹板截面和剪切示意分别见图2、图3。其中,l0为钢腹板投影长度;l为钢腹板直腹板和斜腹板的总长;u为剪切方向的位移;V为剪力。对这2种不同结构体系在集中荷载和均布荷载作用下的挠度进行分析,工况为:①跨中集中荷载作用下的简支梁;②均布荷载作用下的简支梁;③集中荷载作用下的悬臂梁;④均布荷载作用下的悬臂梁。

图2 波形钢腹板截面图3 波形钢腹板剪切示意
国内外的试验及有限元分析结果[14-16]均证明了波形钢腹板组合梁的剪力几乎全部由钢腹板承担。Johnson等[15]推导了钢腹板等效剪切模量Ge的表达式为
Ge=Gsl0/l
(1)
式中,Gs为钢腹板的剪切模量。
1.1 经典梁法
经典梁理论中只计算由弯矩产生的竖向变形,而忽略由剪力产生的剪切变形。计算时假设:①组合截面的转动与混凝土顶底板一致;②不考虑扭转、畸变等行为;③材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;④满足平截面假定。简支梁在集中荷载和均布荷载作用下的挠度计算公式分别为
f=PL3/(48EcIc)
(2)
f=5qL4/(384EcIc)
(3)
式中:Ec为混凝土的弹性模量;Ic为混凝土截面惯性矩;q为均布荷载集度。
1.2 Timoshenko梁法
Timoshenko梁理论中剪力的作用使得相邻截面发生竖向相对滑动,因此发生剪切挠曲。计算时假设:①只考虑波形钢腹板剪切变形;②组合截面的转动与混凝土顶底板一致;③不考虑扭转和畸变行为;④材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;⑤满足拟平截面假定。
文献[4,7-8,10]的挠度计算方法虽然推导过程不同,但均采用这一假设——在弯曲变形的基础上考虑剪切变形,归结为Timoshenko梁理论。简支梁在集中荷载和均布荷载作用下跨中挠度计算公式分别为
(4)
(5)
式中,Aw为钢腹板截面积。
1.3 弹性剪切变形法
贺君等[9]通过假定波形钢腹板梁截面转角的位移场,建立组合梁结构力的平衡条件,引用截面变形相容方程、物理方程,根据不同边界条件推导出简支梁挠曲方程解析解。基本假设为:①只考虑波形钢腹板剪切变形;②组合截面的转动与混凝土顶底板不一致;③不 考虑扭转、畸变等行为;④材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;⑤满足平截面假定。通过考虑跨高比、弯曲刚度、剪切刚度等因素修正解析解,得到简支梁在集中荷载和均布荷载作用下的跨中挠度简化计算公式,分别为
(6)
(7)
1.4 有效刚度法
聂建国等[11-12]运用静力平衡条件,推导出工况1和工况2的挠曲方程解析解;运用变形等效原理简化解析解,得到波形钢腹板组合梁挠度简化计算方法——有效刚度法。该方法基于以下假设:①只考虑波形钢腹板剪切变形;②组合截面的转动与混凝土顶底板一致;③不考虑扭转、畸变等行为;④材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;⑤各自满足平截面假定;⑥纵向受力全部由混凝土承担,不考虑钢腹板的轴向刚度。根据有效刚度法,建立简支梁在集中荷载和均布荷载作用下跨中挠度计算公式分别为
f=PL3/(48B)
(8)
f=5qL4/(384B)
(9)
式中,B为截面有效刚度。
1.5 三角级数理论
与前4种理论相比,三角级数理论[11]具有力学概念清晰、简便适用等特点。基本假设为:①只考虑波形钢腹板剪切变形;②组合截面的转动与混凝土顶底板不一致;③不考虑扭转、畸变等行为;④材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;⑤各自满足平截面假定;⑥纵向受力全部由混凝土承担,不考虑钢腹板的轴向刚度。根据三角级数理论,建立简支梁在集中荷载和均布荷载作用下跨中挠度计算公式分别为
(10)
(11)
式中:S1为顶板截面积,S1=b1t1;S0为钢腹板等效截面的面积,S0=h0tw。
1.6 不同方法的理论差异
5种计算方法的共同点为:①材料线弹性,不考虑混凝土顶底板与钢腹板的滑移及剪力滞后效应;②不考虑扭转、畸变等行为。不同点为:①是否考虑剪切变形。与其他4种理论不同,经典梁理论不考虑剪切挠度对整体挠度的贡献。②截面假定不同。Timoshenko梁计算理论采用的是拟平截面假定[17],即忽略波纹钢腹板的纵向刚度,连接上下翼板纵向线应变则可近似看成平截面假定。其他4种理论均各自满足平截面假定。③剪力的承担范围不同。Timoshenko梁理论和有效刚度理论忽略上下混凝土板对剪切变形的贡献,只考虑钢腹板承担剪力,而经典梁、弹性剪切变形和三角级数理论剪力的承担范围为顶底板和钢腹板。④是否考虑钢腹板对纵向刚度的贡献。有效刚度理论和三角级数理论忽略了钢腹板纵向刚度。⑤公式推导时考虑的基本参数不同。弹性剪切变形法和有效刚度法均运用静力平衡法推导,前者推导的基本参数为梁体竖向挠曲位移、截面剪切角、钢腹板转角,后者则为梁体竖向挠曲位移、翼板中性轴的相对转角。三角级数理论推导的基本参数为梁体竖向挠曲位移、钢腹板转角、翼板转角。
2 算例分析
波形钢腹板组合梁模型材料属性见表1,截面尺寸见图4。波形钢腹板的参数为:t1=40 mm,t2=46 mm,h0=264 mm,b1=900 mm,b2=525 mm,tw=2 mm。为对比不同跨高比下各理论方法的精度,令截面高度不变,跨度分别为1.575,3.500,5.075,7.000,8.750,10.500,12.250,14.000 m。P=20 kN,q=4 kN/m。根据几何尺寸建立有限元模型,考虑顶底板较厚,采用Solid 45实体单元模拟混凝土顶底板,采用Shell 43壳单元模拟钢腹板,边界条件按简支梁和悬臂梁设置,见图5。

表1 波形钢腹板组合梁材料属性

图4 截面尺寸(单位:mm)图5 有限元节段模型
按5种计算方法及有限元法计算得到不同跨高比下4种工况的挠度,分别见表2—表5。按Timoshenko梁理论和有限元法计算得到不同工况剪切挠度占总挠度的比例,见图6。
由表2可知:对于工况1,10

表2 工况1不同跨高比下简支波形钢腹板组合梁剪切挠度

表3 工况2不同跨高比下简支波形钢腹板组合梁剪切挠度

表4 工况3不同跨高比下悬臂波形钢腹板组合梁剪切挠度

表5 工况4不同跨高比下悬臂波形钢腹板组合梁剪切挠度
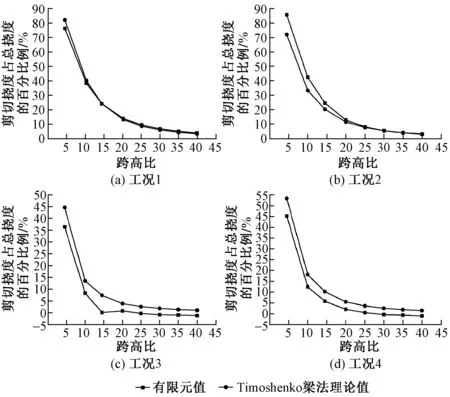
图6 不同工况剪切挠度占总挠度的比例
由表3可知:对于工况2,4.5
由表4可知:对于工况3,4.5
由表5可知:对于工况4,4.5
3 结论
对已有的波形钢腹板组合梁挠度计算方法总结为5种:经典梁法、Timoshenko梁法、弹性剪切变形法、有效刚度法、三角级数理论。对比不同分析方法得到如下结论。
1)5种挠度计算方法的差异在于假设时是否考虑剪切挠度、截面变形假定不同、组合梁剪力承担范围不同、是否考虑钢腹板对纵向刚度的贡献、公式推导考虑的关键参数不同。
2)4种工况在不同跨高比区间适用的挠度计算方法分别为:工况1,L/H>10时推荐采用Timoshenko梁法;工况2,L/H>14.5时推荐采用Timoshenko梁法;工况3,L/H≥4.5时推荐采用三角级数理论;工况4,L/H≥4.5时推荐采用三角级数理论。建议4种工况考虑剪切变形的跨高比限值分别取35,35,10,14.5。

