指向学生发展核心素养的数学概念教学

孙晓华 朱峰

摘要：概念的建立，不是概念术语的机械识记过程，也不是单纯的直观形象的简单累积过程，而是基于概念本质内涵的意义建构过程。以小学数学中“面积”概念教学为例，通过创设情境、激发需求、举一反三，从面有多大，到面积是多少，让学生经历从模糊到逐渐明晰的过程，内化面积概念本质。

关键词：概念教学;面积;本质内涵;数学思考;核心素养

中图分类号：G633.63 文献标志码：A 文章编号：1673-9094（2019）02B-0095-04

史宁中教授指出：“基于核心素养的教学，要求教师要抓住知识的本质，创设合适的教学情境，启发学生思考，让学生在掌握所学知识技能的同时，感悟知识的本质，积累思维和实践的经验，形成和发展核心素养。”[1]基于此，在发展学生核心素养的素质教育当下，进行概念教学时，概念的建立，既不是概念术语的机械识记过程，也不是单纯的直观形象的简单累积过程，而应该是基于概念本质内涵的意义建构过程[2]。下面以小学数学中的“面积”概念为例，探讨如何开展指向学生发展核心素养的概念教学。

一、面积的本质内涵

关于“面积”这一概念的本质究竟是什么？《辞海》（第六版）里的解释是：“几何学的基本度量单位之一。是用以度量平面或曲面上一块区域大小的正数。通常以边长为单位长的正方形的面积为度量单位。”这一解释也并不是一个严格的定义，现代数学中的测度理论中给出了面积的一个严格定义[3]：

【面积】设Σ是一些封闭平面图形组成的集合。m是定义在Σ上取值于非负数的一个映射：m（A），A∈Σ，且满足以下条件：

1.（有限可加性）若A，B ∈ Σ，A与B不相交，那么m（A∪B）=m（A）+m（B）。

2.（运动不变性）如果图形A ∈ Σ，经过平移、旋转、反射的运动成为图形A' ∈ Σ，那么m（A）=m（A'）。

3.（正则性）边长为1的正方形I ∈ Σ，且m（I）=1。

我们称映射m为图形的面积。

无论是《辞海》，还是现代数学中的测度理论，都阐释出面积的本质是一个数，即用一个数来表达“一个区域的大小”。张奠宙教授指出，在教学参考资料以及小学数学教师培训教材中，面积可定义为：数m是一个平面图形A的面积，就是指能用m个单位正方形不重叠地恰好填满A[4]。他的理解依然突出了“面积是一个数”的本质表达。

而大多数教科书中都是说：“物体表面或封闭图形的大小就是它们的面积。”并没有对面积下严格规范的定义，常常采用的是描述性的定义。在小学数学面积的教学中，我们不妨分解出若干个子概念：区域、大小和数，逐层递进，由模糊至清晰，揭示面积的本质内涵。其中，区域的大小属于表象，即所谓的面和面的大小;而當面的大小上升到用数来表示时，那就完成了概念的高度抽象和简洁化的数学表达。

二、面积本质解读的教学实践

（一）创设情境，引导学生寻找方法比较面积大小

数学概念都是抽象思维的产物，这一特性决定了学生的概念学习一般都要以相应的感性经验为基础[5]。要使学生对面积的认知直达深入，首先得充分利用实际情境，引导学生寻找比较面积大小的方法，建立“区域大小”的表象，把“面有多大”贯穿始终。

1.创设圈地情境，实现由线到面的初步转换

面积和长度一样，都是度量概念，而在此之前，学生脑海中的长度概念已经根深蒂固，所以从线到面是一个概念向另一个概念的根本转变。为此，创设辨析情境必不可少。

【情境】熊大和熊二在开心农场的草莓园采草莓。按采摘规则：每人用一根同样长的绳子，圈出一块长方形的地，被圈中的草莓才能采摘。兄弟俩迫不及待地拿起绳子去圈草莓了。结果发现：明明是一样长的绳子圈的地，草莓的长势也差不多，为什么熊二采到的草莓比熊大多很多呢？

以上情境旨在引发学生的数学思考：这两块地有什么相同的地方？又有什么不同之处呢？——周长相同，但形状不同，大小也不同。学生对“大小”的捕捉，启发教师进一步追问：你能来指指它们的大小吗？学生自觉地用“摸”这一动作，意味着他们的视角已经从线转到了面，摸的是这两块地的面，继而进一步用规范的方法摸一摸树叶的面、课桌的面，冰箱上的面，屏幕的面、苹果的面、魔方的面……不同的面的感觉自然而然在指尖流淌——数学课本的封面比我的手掌大;有的面大，有的面小;有的面是平的，有的面是弯曲的;有的面是规则的，有的面是不规则的……这些丰富的事例中均蕴含着对“面是有大有小”的感知。

2.寻找比较方法，实现“面有多大”的初步感悟

当学生借助摸一摸，对“面”有了“区域”的感觉，那么这块区域的大和小的感悟用什么方式来表达呢？也就是怎样来说明面有多大呢？凭借学生已有的认知状态，可以分两个层次：

（1）肢体语言的比划。黑板的面有这么大;课本封面有这么大。直观动作传达了对面的大小的直觉感知，由此带动学生边比划边进一步提炼：黑板面的大小是黑板面的面积;课本封面的大小是课本封面的面积。

（2）直观方式的比较。利用观察法、重叠法等等，或者直接的视觉感知、或者动手操作后的触觉带动视觉的感知，让学生对面积的感悟不仅仅是停留在字面的表达上，而是触及了概念表象的根本。

图1中的图形①和图形②，“虽然我们不知道它们的面积到底有多大，但通过观察，一眼就能比出它们的大小”。图2中的图形③和图形④“重叠后，大面积把小面积包含在了里面”。“大小”“包含”这些词汇，传达出学生在不同方法的比较中，由具体实物到平面图形，对面积的“大”和“小”形成了未经理性分析的直觉形象。

（二）激发需求，引导学生运用单位面积比较面积大小

有效的概念教学就是抓住其本质属性，促进学生对概念内涵的深刻理解，并经过简约化的提炼进行符号化的数学表达。面积的本质是用一个数来表达“面的大小”，当对“面的大小”的感悟由原来的直观感知上升到理性描述，那么面积的本质在数学化的表达中就形成了概括性的抽象概念。这时候的教学过程，就需要一个恰当的时机，让学生产生用精准的数学化方式描述“面有多大”的需求。

第一，通过上述比较，学生积累了一定的比较面积大小的直观经验。在此基础上，呈现图3中的图形⑤、图形⑥，继续比一比谁的面积大谁的面积小。显然学生会费一番周折。直接观察？不行！重叠？也不行！在一次次尝试中，会有学生想到剪拼。如果凑巧，像下面图4剪拼图一般，剪拼三四次，可以比出大小了;而若不凑巧，也许剪拼七八次都比不出。这时，学生会产生强烈的感觉——太麻烦了！显然这是寻找新的比较方法的第一层需求。

第二，学生急需要一根突破固有模式的拐杖。生活中人们的做法——用拃来测量和比较两根绳子的长短、用碗来测量和比较两袋大米的轻重启发了学生：既然用一个确定的小长度量出大长度是多少可以比出长短，用一个确定的小质量去量出大质量是多少从而可比出轻重，那么现在能不能也通过确定一个小面积有多大继而量出大面积里包含了多少个小面积呢？学生由此产生了新的需求，去寻找一个小面积。

第三，学生用圆形、三角形、正方形等纸片如图5般去尝试，发现小正方形正好不重叠地填满长方形。最终他们达成共识：用小正方形来测量大长方形的面积，左边的长方形有16个小正方形那么大，右边的长方形有15个小正方形那么大。突破层层认知冲突，学生拨云见日——用小面积量出大面积是多少，从而比出了面积的大小。面积大小的直观感知被抽象到“多少”个小正方形的精准化描述，即一个区域的大小有多少个面积单位。

第四，在对面积的概念完成初步抽象的基础上，进一步用确定大小的小正方形去测量不同图形的面积：如果设定单位大小的小正方形面积为“1”，那么不同图形的面积可以用谁来表示呢？这时候，学生把图形放入每格面积为“1”的方格图中，借助平移、旋转等运动，数一数得到了一个个确定的数，这时，面积的运动不变性和有限可加性被体现出来，面积是一个数的内涵得到丰厚，同时面积的本质得以高度抽象和概括，即完成了用“数”来描述“形”。

（三）举一反三，引导学生灵活解决比较面积大小问题，结面积本质之果

数学概念形成的发展过程是一个数学化的精加工过程，即对丰富的材料进行细致的观察，借助分析、综合、比较、抽象等思维活动，抽象出共同的、本质的数学属性[6]。此外，还需要在合乎逻辑法则的条件下操作运用抽象的数学知识与数学方法（包括数学符号及语言的运用）去处理数学问题，并进一步去发展数学理论知识[7]，从而形成完整的认知结构，拓展外延的同时进一步深化概念内涵，发展核心素养。所以，当面积的大小用最简约的数来概括时，我们还应该把视角指向更远的深处，举一反三，引导学生灵活解决比较面积大小的问题，结概念本质之果。

问题1：是不是所有图形的面积都能用一个数来表示呢？

围绕这个问题展开如下研究性学习：

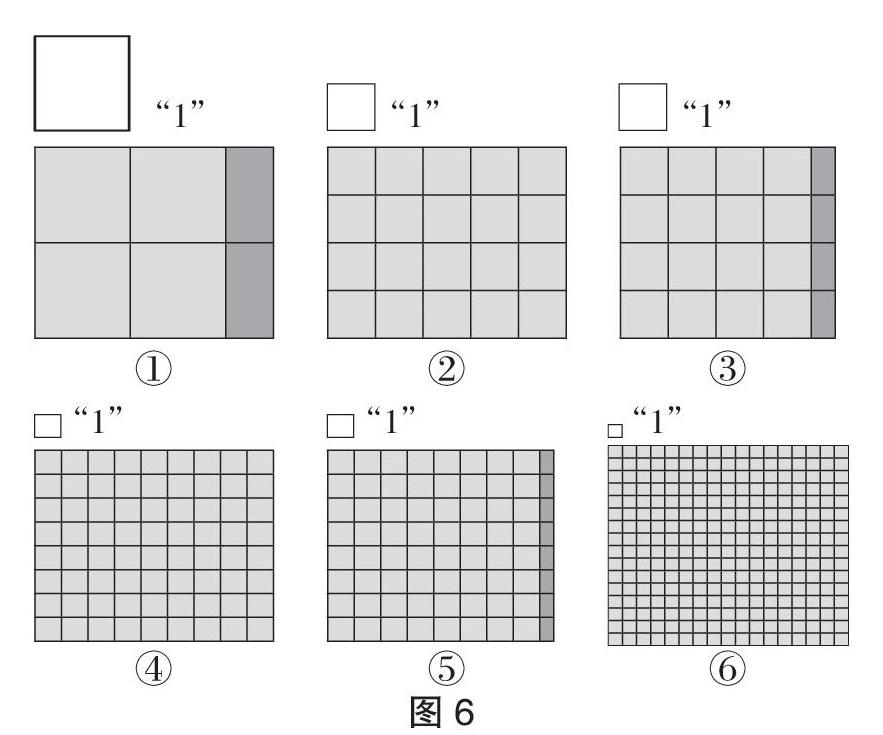
师（出示图6①）：如果这样的小正方形的面积表示1，那么大长方形的面积是多少？

生：有不满一格的，不能确定。

师：对啊，有不满一格的怎么办？

生1：看看能不能湊成一格。

生2：可以选择小一点的正方形去测。

师（出示图6②）：如果这个小一点的正方形的面积表示1，那么现在你能数出长方形的面积是多大了吗？

生：20。

师（出示图6③）：如果用这样的小正方形还是不能铺满怎么办？

生：选择更小的小正方形来测量。

师（出示图6④）：如果这么小的正方形的面积表示1，那么现在这个长方形的面积是多少？

生：72。

（依次往下到图6⑤、图6⑥……）

师：按这样的规律继续往下分，请同学们想一想：可以得到多少个小正方形？

小正方形会越来越接近什么？如果它是一个数，会越来越接近几？

生：小正方形越来越接近一个点，如果它是一个数，会越来越接近0。

在以上过程中，学生的思维向深处漫溯。首先，面积的本质特性得以充分凸显（尤其是正则性）。其次，学生借助一组图形发现，单位正方形可动态变化，任何一个单位正方形，通过细分可得到无限个更小的正方形，为后续学习长方形的面积公式m=ab，当a，b不是整数时，要用边长是0.1，0.01……的单位正方形去填的思维启迪埋下伏笔。再次，渗透极限思想。

问题2：生活中不规则的土地，可以怎样来比较它们的面积呢？

为了深化面积的本质内涵，并进一步加深对面积特性的理解，可以创设如下情境：

吉吉和毛毛来到了开心农场，它们找到了三片桃园（如右图）。采桃子的规则是：第一个人可以任选一片桃园，第二个拿剩下的两片桃园。吉吉说：“我是国王，我先选，我选那片最大的桃园。”毛毛说：“那好吧。”于是，剩下的两片桃园就归毛毛了。

师：你们觉得吉吉挑这片桃园占便宜了吗？你有什么方法验证？

生1：可以把这三片桃园叠在一起比一比。

（学生利用白板软件把两片小桃园拼接在一起，再和最大的那片桃园重叠在一起比）

生2：也可以用小正方形去填。

师：如果用小正方形填了还是比不出怎么办？

生：那就用更小的小正方形去填。

师：同学们的这种想法能不能解决问题呢？大家可以课后去思考。

从“面积有多大”到“面积是多少”，从运动不变性、有限可加性再到正则性，举一反三，理解与运用、联结与比较，从不同的视角思考并解决问题，面积的本质内涵和特性在学生思维的不断碰撞中得以内化，进而也将发展学生的核心素养落到实处。

参考文献：

[1]史宁中.推进基于学科核心素养的教学改革[J].中小学管理， 2016（2）：19-21.

[2]朱德江.“学”与“导”应着力于学习的关键点——“认识面积”教学实践与思考[J].小学数学教师， 2016（3）：20-24.

[3][4]张奠宙.深入浅出，平易近人——怎样测量长度、面积和体积[J].小学教学（数学版）， 2014（9）：4-6.

[5]钱坤南.经历体验过程  促进概念理解——以苏教版《认识面积》为例[J].江苏教育研究， 2014（12B）：52-54.

[6]孙晓华，朱峰.深入简出，实现概念精加工[J].江苏教育研究， 2013（11B）：41-43.

[7]王名扬，徐沥泉，徐利治.论一种缘自认知心理学及教育学研究的数学认知过程[J].数学教育学报， 2013（1）：33-36.

责任编辑：朱忠明