放缩法在数列不等式证明中的应用

☉湖北省武汉市建港中学 陈远秀

一、考情分析

1.关注以下几个递推关系

（1）已知a1，且an+1=pan+q（p，q为常数）；

（2）已知a1，且an+1=pan+f（n）（p为常数，f（n）为一次函数、二次函数或指数函数）；

（3）已知a1，且an+1=f（n）an；

（4）已知a1，且（a，b，c，d为常数）；

（5）已知a1，a2，且an+2=pan+qan+1（p，q为常数）.

2.在解决数列与不等式问题时，常常会用到以下放缩模型

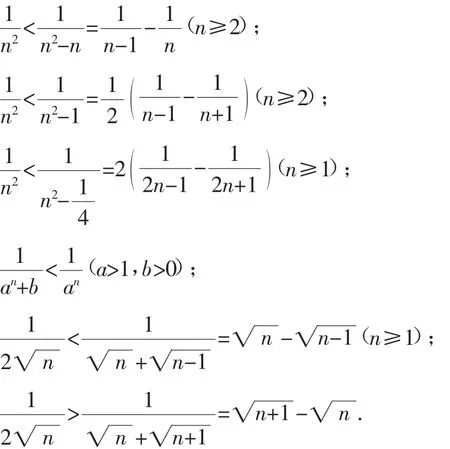
（3）利用一个不等式的恒成立问题“若a＞1，b＞0，c＞0且a＞b时，不等式对n≥m且m，n∈N*恒成立，求实数λ的取值范围”进行放缩.

上面这个不等式恒成立模型可拓展成：“若a＞1，b＞0，c＞0且a＞b时，不等式对n≥m且m，n∈N*恒成立，求实数λ的取值范围”，用同样的方法来操作即可求解.

二、考题再现

1.（2015年浙江高考数学理）已知数列{an}满足且an+1=an-an2（n∈N*）.

（2）设数列{an2}的前n项和为Sn，证明：

2.（2015年重庆高考数学理）在数列{an}中，a1=3，an+1an+λan+1+μan2=0（n∈N*）.

（1）若λ=0，μ=-2，求数列{an}的通项公式；

三、典例探讨

例1已知数列{an}的前n项和Sn，满足：an+Sn=1.（1）求数列{an}的通项公式.

解：（1）由an+Sn=1退一位得an-1+Sn-1=1（n≥2），两式相减可得：2an=an-1，

所以数列{an}为等比数列.所以

①当n=1时

当n≥2时所以当n≥2时，Tn=c1+c2+c3+…+cn≤1+

②当n=1时

当n≥2时，

当n≥3时，令

所以当n≥3时

所以当n≥3时

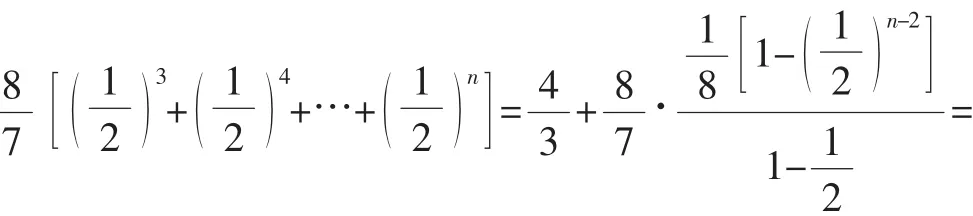
例2设数列{an}满足a1=a，an+1an-an2=1（n∈N*）.

（1）若，求实数a的值；

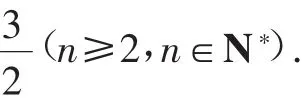
因为，所以可得

若，则a无实数解，

由a2=2可得a=1成立，所以a=1.

（2）因为当n≥2时

所以当n≥2时

所以an2≥2+2（n-1），即an2≥2n.

所以

因为an2≥2n，所以当n≥2时