心中有丘壑,笔下生云烟
——以对称视角下的错解分析为例
☉山东省临清市京华中学 齐 欣
参考文献[1]指出体会对称之美,欣赏对称之妙,是贯穿在整个学习过程中的.参考文献[2]指出,对称是一种审美心向下的思维走势,是一种方向性引领,引领我们走出困境,走向澄明.笔者深受启发,结合教学实践及阅读参考文献[3]的思考,基于两个案例,分析解题过程中的错因,注重学生对其中蕴含的数学本质的理解,才能让学生领悟解题的真谛,达到“吃一堑,长一智”的目的,还要引导学生体会解题纠错中渗透的方法、蕴含的哲理.
一、纠错案例展示
案例1:(2016年成都卷第24题)实数a、n、m、b满足a<n<m<b,这四个数在数轴上对应的点分别是A、N、M、B(如图1),若AM2=BM·AB,BN2=AN·AB,则称m为a、b的“黄金大数”,n为a、b的“黄金小数”.当b-a=2时,a、b的黄金大数与黄金小数之差m-n=______.

图1
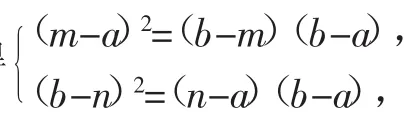
学生的困惑:此法先把各线段的长用代数式表示出来,再分别代入到已知条件中,列出方程组求解,这个答案显然违背题意,这到底是什么原因呢?
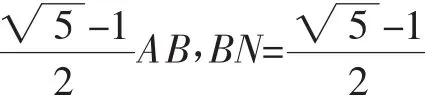

对于本题,还可以求出AB,然后列出关于AM、BN的方程,再求解.把已知AM2=BM·AB及BN2=AN·AB看作关于AM(或BM)或AN(或BN)的一元二次方程,即可求出线段AB上任意一条线段.
另解1:由AM2=BM·AB,BM=AB-AM,得AM2=(ABAM)·AB.又AB=b-a=2,则AM2=(2-AM)×2,解得AM=-1.根据对称性,得BN=-1.则MN=AM+BNAB=2-4.
另解2:设MN=x,AN=y,则(x+y)2=2(2-x-y).将“x+y”视为整体,整理得(x+y+1)2=5,解得x+y=-1(负值不合题意,舍去).所以MB=2-(x+y)=3-.根据对称性,得AN=3-.所以MN=AB-AN-MB=2-(3-)-(3-)=-4.
尽管得到的“答案”很明显是错误的,但查找错因并不那么容易.通过严谨的数学思考和基于对称视角分析,不仅查明了真相,还收获了借助对称性来思考问题,及对称观念引领下的简单解法,可谓一举多得,下面再看一例.
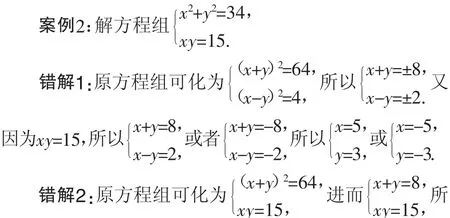

学生的困惑:错解1、2的解是怎样丢掉的?错解3怎么多了四个解呢?
错因分析:第一个学生“由xy=15,得到x、y同号,进而想当然推出x+y与x-y也同号,从而丢掉了两个解”.事实上,x、y同为正数或x、y同为负数;当x、y同为正数时,可以得到x、y的和是正数,但x、y的差呢?并不一定是正数啊.同样,当x、y同为负数时,x、y的和是负数,但x、y的差也不一定是负数.第二个学生忽视“正数有两个平方根……”这一平方根的性质.第三个学生“解方程组的过程中,第2个方程两边平方了,因此求得方程组的解之后,必须代入原方程组进行检验,因此结合x、y必须取同号的值,必须舍掉异号的四个解”.在解题过程中,应随时注意整体与局部的关系,不能以局部的性质代替整体,从而有效规避错误.

学生如有从对称的角度分析问题的意识,则成功解题易如反掌,对称在数学解题中的应用不胜枚举.如2014年泰州卷第16题:
如图2,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC交于点P、Q.若PQ=AE,则AP等于______cm.

图2
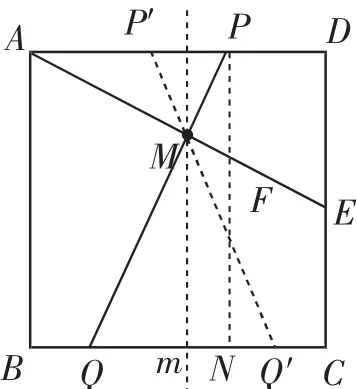
图3
赏析:如果能从对称的视角来理解则事半功倍(如图3,两次利用对称,第一次是P′Q′与PQ关于直线m对称,第二次是AP′与PD对称),否则,要么容易忽视“确定性”或因思维定式导致丢解,要么事倍功半,即使做出来了,也耗时过多,造成“隐性丢分”,得不偿失.关于本题的研究,钱德春老师在参考文献[4]中已有详细论述,这里不再赘述.
又如概率中用列表法和树状图法求概率,列出的表格和树状图从数学的角度来看是对称的.
如图4,一只蚂蚁自由自在地在用七巧板拼成的正方形中爬来爬去(每一块的表面完全相同).
(1)分别计算它最终停留在1号板和2号板上的概率;
(2)它最终停留在3号板上的概率是多少?
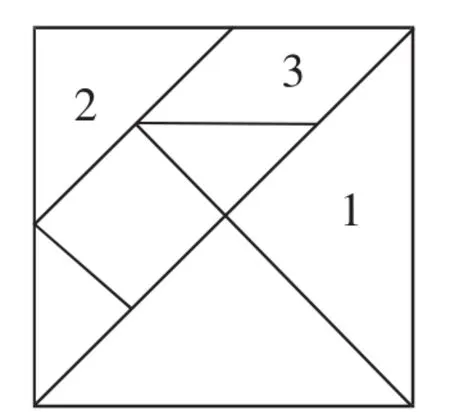
图4
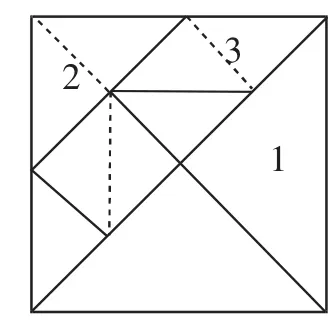
图5
分析:如图5,加上这三条辅助线后,借助对称便直观地看出停在2、3号板上的概率分别是多少了.
又如,求满足(n+1)n2-2n-3=1的整数.
错解:由x0=1,x≠0,得n2-2n-3=0,且n+1≠0,解得n=3.
分析:对于ab=1,上述解法只考虑了非零数的零次方等于1,而忽略了底数n+1等于1(指数为任意数)和-1(指数为偶数)的情况.如果想象有一条数轴,那么1、-1是关于原点对称的.
总之,对称,是观念,也是方法,是一种或图或式的灵活运用,在对称视角下辨析错因,澄清了错误,走出了困惑,同时开阔了视野,丰富了解题思路.
二、教学建议
1.解题教学要理解基础知识,重视等价转化,探索一题多解
通过对错解引发的一题多解的分析,发现学生的学习问题,其根源是没有重视等价转化,思考不严密或基础知识不扎实.转化有等价转化与非等价转化两种形式.等价转化要求转化过程中前因后果是充分必要的,才能保证转化后的结果仍为原问题的结果.非等价转化其过程是充分或必要的,要对结论进行必要的修正(如分式方程化为整式方程可能会出现增根,因此要验根),它能给人带来思维的闪光点,找到解决问题的突破口.但是一定要注意转化的等价性与非等价性的不同要求,实施等价转化时确保其等价性,保证逻辑上的正确(如案例1中的错解,看似经得起推敲却百密一疏,又如案例2及参考文献[3]中对“解”的“纯粹性”与“完备性”的分析).等价转化思想方法是高中数学解题的基本方法,在历年高考中也常见,因此我们要不断培养和训练学生自觉的转化意识,这有利于强化解决数学问题中的应变能力,提高思维能力和技能、技巧.
2.解题要让学生学会自觉分析,揭示数学本质
学生解题水平取决于对知识本质的理解.案例1、案例2及参考文献[3]中的错解,这些错误产生的原因都是隐性的.罗增儒教授说过数学解题不仅要关注“答案”,更要对过程进行“自觉分析”.因此数学解题要让学生养成自觉分析、反思质疑的良好习惯.从核心知识和概念入手,深挖教材,设计核心例题,充分揭示数学本质(如本文中的对称思想、等价转化思想等).站在教育者的角度,数学本质应该包括数与形的客观规律,知识所处的背景、地位、作用、联系、区别及其蕴含的数学思想方法、思维过程.
3.解题教学要揭示数学思想方法与思维的形成
解题教学要推动学生经历知识的形成过程,引导学生发现数学规律、知识的内在联系和问题的解决途径,促进数学思维的正迁移,渗透学习方法,转换视角,借助数学思想化错、融错、究错,使学生在科学精神、思维能力、情感态度与价值观等方面得到进步;体会解决问题的过程,学会数学的表达和交流,积累经验;在掌握“四基”的同时提高数学素养,实现更高层次的思维突破.
4.解题要注重生成,教学相长
数学问题都是运用所学过的知识加以解决的,知识转化才是一切转化思想与方法的本源.学生参与的解题活动不仅包括外显的、可观察的解题过程,也包括学生积极展示内隐的思维活动.作为一线教师,要想让学生做到“吃一堑,长一智”,不仅要会讲授,更要学会“倾听”,要大胆放手,让学生尝试.布鲁纳说过:“学生的错误都是有价值的.”著名教育家卡尔·威特的教育秘诀之一,就是宽容地、理性地看待孩子的一切,包括错误.错误也从一定角度反映出学生对知识的掌握程度及暴露出来的教与学方面存在的问题.因此要善待学生的出错,让错误成为转机,充分体现转化思想,重视生成性资源的教学,采用逐步深入纠错的方法,让学生乐于纠错,踏实纠错.学生的主动好学定能让数学课堂出彩.在教学中要教会学生进行错解分析,挖掘错误的根源,从而巩固和加深基础知识,真正做到教学相长.总之,通过辨析错解产生的原因,训练学生思维的严谨性、深刻性、灵活性、批判性与独创性,使学生的数学素养得到提升.以上论述还很粗浅,希望得到批评与指正.

