由一道模拟向量题的最值问题解法及变式引发的思考

☉安徽省宁国市津河中学 汪庭斌

涉及平面向量的最值问题一直是高考平面向量部分比较常见的考查形式，往往涉及向量的模、向量的夹角、向量的数量积、参数值等相关最值的求解，也是各类模拟卷、自主招生中比较常见的题型.此类问题的切入点多，方法多样，而且难度一般都不低，是知识的交汇点，其创新应用强，能力体现高，是数学素养培养与提升的重要场所.

例在边长为1的正三角形ABC中，E，F分别是边AB，AC上的动点，且满足，其中m，n∈（0，1），m+n=，N分别是EF，BC的中点，则|MN|的最小值为（ ）.

本题以“E，F分别是边AB，AC上的动点”这个“变”的关系与“这个“不变”的式子来设置，结合“M，N分别是EF，BC的中点”，利用其中点M的“动”与点N的“不动”这一对关系来确定“|MN|的最小值”.充分体现了动与静，变与不变，常值与最值等矛盾与统一的辩证关系，也充分联系起平面向量、函数、几何等知识点之间的交汇与综合，可以达到综合考查能力，培养素养品质的目的.

基底法是解决平面向量的常用方法与常见技巧，一定要熟练掌握.其本质是通过平面向量的线性关系理清向量之间的关系，把所要求解的|MN|转化为相应的基底向量的线性关系，然后利用模的平方建立起含有参数m，n的关系式，并结合两参数之间的关系加以转化，化为只有其中一个参数的二次函数问题，最后利用二次函数的图像与性质来确定最值即可.

解法1：由于M，N分别是EF，BC的中点，

共线向量定理是平面向量中关于平面向量线性关系的一个重要定理，可以有效构建起平面向量的线性关系与相关三点之间的位置关系.借助平面向量的中点公式加以转化，构造出新的点G、H，并结合共线向量定理可以确定点M的轨迹为线段GH（不包括两边的端点），再利用平面几何性质来确定|MN|的最小值.

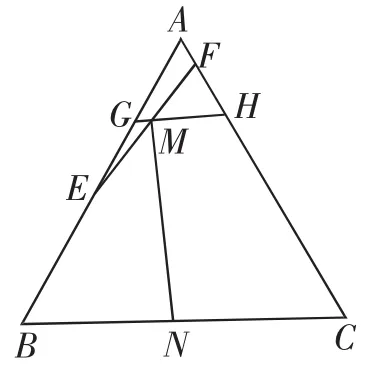
图1

解法2：由题n，又由于M是EF的中点，则有n

因此根据共线向量定理可知点M的轨迹为线段GH（不包括两边的端点），

又根据平面几何性质可知当点M为线段GH的中点时，|MN|取得最小值，其值为正三角形ABC的高的

在破解一些有关平面几何问题的选择题时，经常可以利用平面几何的一些相关基本性质，选取特殊位置来进行特殊化处理，进而得以快捷处理并正确破解.这里利用正三角形ABC的图形的对称性可知，最值处必定是在相应的平衡位置，由此确定两参数m，n相等，进而确定 |MN|为正三角形ABC的高的，再结合三角形的性质得以快捷处理.

解法3：根据正三角形ABC的图形的对称性可知，最小值只可能产生于平衡位置，

三、变式拓展

变式方向1：改变两参数m，n的和为其他满足条件的常值，其他条件均不变，进行变式拓展.

变式1：在边长为1的正三角形ABC中，E，F分别是边AB，AC上的动点，且满足，其中m，n∈（0，1），m+n=1，M，N分别是EF，BC的中点，则|MN|的最小值为（ ）.

变式方向2：改变两参数m，n的和为一般性的满足条件的参数，其他条件均不变，进行变式拓展.

变式2：在边长为1的正三角形ABC中，E，F分别是边AB，AC上的动点，且满足n∈（0，1），m+n=λ∈（0，1），M，N分别是EF，BC的中点，则|MN|的最小值为______.

解析：由于M，N分别是EF，BC的中点，

在解答涉及平面向量的最值问题时，关键是要正确把握题目条件，从题意入手，从平面向量的相关概念与相关运算的本质出发，选取代数与几何、数与形等方式，用向量法、几何法、函数法、三角法、图像法、不等式法等行之有效的基本方法来解决，进而达到解决相关最值问题的目的.