问题引领课堂 驱动自主探究

江苏省苏州市吴中区迎春中学(215128) 沈萍

问题是教学的心脏,也是思维活动的起点.课堂上精心设计的问题能激发学生学习兴趣,集中学生注意力,调动学生积极性,还可以驱动学生自主探究,独立思考,从而启迪学生思维.合理设计的问题,能充分体现“以教师为主导,学生为主体”的教学原则,使课堂教学达到事半功倍的效果.笔者针对如何进行问题设计,培养学生自主探究能力,作了以下尝试.

一、问题设计趣味化

问题设计趣味化,能够提高学生的学习兴趣,驱动学生进行自主探究、合作交流.因此课堂中教师把问题设计得生动、有趣,可以激发学生的好奇心和学习热情,从而激励学生自主探索,提高学生分析和解决问题的能力.

案例1在讲“用一元一次方程解决问题”时,笔者设计了以下趣味性问题引入,这样可以快速抓住学生的注意力,驱动学生自主探究.

以下诗出于清朝数学家徐子云的著作,请算出诗中有多少僧人?

巍巍古寺在云中,不知寺内多少僧.三百六十四只碗,看看用尽不差争.三人共食一只碗,四人共吃一碗羹.请问先生明算者,算来寺内几多僧?

分析三人共食一只碗:则吃饭时一人用三分之一个碗;四人共吃一碗羹:则吃羹时一人用四分之一个碗.两项合计,则每人用个碗.设共有和尚x人,依题意得:=364, 解之得,x=624.

案例2在讲“有理数混合运算”时,笔者设计了趣味性的游戏“升级版24点”.“24点”游戏是学生以前就玩过的游戏,贴近学生生活,所以深受学生喜欢.

“升级版24点”:请用加、减、乘、除和乘方中的若干种运算(可用括号)将以下有理数(2,3,-3,5)列成算式,使得计算结果为24.(底数、指数都从这4个数中选)

设计趣题和趣味性的游戏都能快速吸引学生的注意力,激发学生积极思考,使思维处于活跃状态,创造潜能得以发展,同时也能培养学生自主探究的能力,提高课堂效率.

二、问题设计真实化

问题设计真实化,即问题情境源于生活实际.生活中的实际问题,学生看的见、摸得着.联系生活实际可以让学生感受到数学就在我们身边,从而充分调动学生的学习积极性.问题设计真实化可以将学习的问题镶嵌于真实的情境之中,让学生自主提问,从学生关注的问题入手,更能驱动学生自主探究.

案例3在讲“7.6用锐角三角函数解决问题”时,笔者设计了学生较为熟悉的“摩天轮问题”,摩天轮是学生很感兴趣,而且大多数学生也都坐过的.在出示例题之前,我设计了以下问题:

师:大家在坐摩天轮时比较关心什么问题?

生1:我关心距离地面的高度.

生2:我关心离开地面的时间.

生3:我关心到达最高点的时间

……

师:在坐摩天轮时,我们最关注的主要是时间和高度.那么接下来我们就一起研究一下同学们关心的问题.

例题游乐场的大型摩天轮半径为20m,旋转1周需要12min.我们从摩天轮的底部(与地面相距0.3m).

问题1:经过2min后我们离地面的高度是多少?

问题2:摩天轮转动多长时间后,我们离地面的高度将首次达到15.3m?

问题3:摩天轮转动1周,小明将有多长时间连续保持在离地面不低于30.3m的空中?

利用生活中的素材(摩天轮),从学生最关注的问题(时间和高度)入手,巧妙设疑,让数学贴近生活,提高了学生的学习兴趣,也激发了学生自主探究的热情.学生在分析和探究实际问题的过程中,把实际问题抽象成数学问题,用数学模型解决问题,从而培养了学生自主探究能力.待问题解决后,学生会产生强烈的成就感和自豪感.

三、问题设计变式化

问题设计过程中一定要进行变式设计,通过改变题目中的关键词,将题目“改头换面”,既能激发学生的探究兴趣,提高了学生的学习热情,驱动学生自主探究,又能打破学生的思维定式,增加学生的应变能力,提高了学生阅读能力及分析解决问题的能力.

案例4如图1,△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点D为AB中点,点O为AC上一点,以O为圆心,半径为1cm的圆与AB相切,点E为切点.

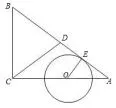
图1

(1)求线段AO的长;

(2)若将⊙O以1cm/s的速度移动,移动中的圆心记为P,点P沿O→C→B的路径运动,设移动的时间为t(s),则当t为何值时,⊙P与直线CD相切?

分析(1)利用△AOE∽△ABC,可得AO的长度;

(2)关键句“点P沿O→C→B的路径运动”,因此要使⊙P与直线CD相切,则有两种情形①点P在线段OC上(见图2)②点P在线段BC上(见图3).

变式1若将⊙O以1cm/s的速度移动,移动中的圆心记为P,点P沿O→C→B→A的路径运动,设移动的时间为t(s),则当t为何值时,⊙P与直线CD相切?

变式2若将⊙O以1cm/s的速度移动,移动中的圆心记为P,点P沿O→C→B→A的路径运动,设移动的时间为t(s),则当t为何值时,⊙P与线段CD相切?

图2

图3

图4

图5

第(2)问结束后,笔者设置了两个变式.变式1中点P的运动路径变为“O→C→B→A”,因此除了图2、图3两种情形,还有图4、图5共4种情况.变式2除了点P的运动路径变为“O→C→B→A”外,“直线CD”也变为了“线段CD”,因此有图2、图3、图4共3种情况.通过进行问题变式化,引导学生观察变式与原题发生了怎样的变化,从而激发学生的学习热情,驱动学生自主探究,提高学生的阅读能力.

变式化的问题设计拓展和加深学生的知识层面,培养学生创新能力和自主探究能力,对提高学生思维辩证能力,拓展解题渠道,都有不可替代的作用.

四、问题设计层次化

问题设计层次化,即通过设计环环相扣,由易到难,由浅入深,循序渐进的数学问题串,使不同层次的学生能解决不同层次的问题,从而使全体学生主动地参与数学学习的活动中去.层次化的问题设计,还可以将难点分散,减缓问题的难度,也能激活不同思维程度的学生思维,驱动学生自主探究.

案例5在上“二次函数综合”的习题课时,我将湖北省鄂州市2017年中考题进行了改编,设计了一系列的问题串.

已知:如图6,抛物线y=ax2+bx+c与x轴交于A(3,0)、B两点,与y轴交于点C(0,3),抛物线的对称轴是直线x=1,D为抛物线的顶点.

图6

(1)求抛物线的解析式及顶点的坐标;

(2)连接CA、DC、AD,判断△ACD的形状;

(3)y轴上的点E在点C上方,且CE=0.5,求证:直线DE是△ACD外接圆的切线;

(4)点P为在直线AC上方的抛物线上一点,设P点横坐标为m,△ACP的面积为S,

①试写出S与m的函数关系式,并求出S的最大值;

②在直线AC上方的抛物线上找一点P,使S△ACP=求点P的坐标.

第(1)问的设计起点低,基础性强,对于基础较薄弱的学生都能解决.本题考查用待定系数法求抛物线的解析式,也为后面的问题做好铺垫.

第(2)问原中考题上没有,笔者为了给第(3)问搭建阶梯而设计的.如图7,学生基本上是可以猜想出△ACD是直角三角形.对于证明直角,有以下两种方法:

法一用勾股定理逆定理,即算出DC==3DA=2则可证出DC2+AC2=AD2,所以△ACD是以∠ACD为直角的直角三角形.对于中等或中等偏下水平的学生都能用这个方法解决的.

法二笔者设计这样的问题,引导学生自主探究,突破自己的最近发展区,发散思维,达到优解的目的.

师:利用本题的已知点A(3,0)、C(0,3),可以想到OA、OC有什么关系?

生:OC=OA=3,即∠OCA=45°,

师:要证∠DCA=90°则只需证明什么?

生:∠DCM=45°.

师:如何证明∠DCM=45°?

生:由DM=MC=1,可证∠DCM=45°,所以∠DCA=90°.这种方法更简单.

图7

图8

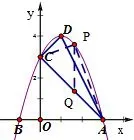
图9

第(3)问难度加大,针对中等偏上水平的学生.如图8,证明直线DE是△ACD外接圆的切线,这个问题设置有些抽象,图中无圆,要求学生做到心中有圆,要证明切线,那么圆心和垂直则成为问题的关键.第(2)问的设置,可化解第(3)问的难点,△ACD为直角三角形的证明,一方面可确定Rt△ACD的外心在斜边AD中点上,即AD为Rt△ACD外接圆的直径;另一方面为证明DE⊥AE提供方法.

第(4)问难度更大,主要针对优等生.如图9,②为原题,难点在于解决△ACP的面积.为了化解难点,我设置了①.△ACP为“斜三角形”,为了化斜为直,引导学生想到分割图形的方法,即过点P作PQ//y轴,将△ACP分割成△QCP和△AQP,由于PQ为公共底,想到表示PQ,而PQ的长度与点P和点Q的纵坐标有关,由此想到将P、Q的坐标表示出来.P在抛物线上,Q在直线AC上,所以要先求直线AC的解析式.PQ表示出来,△ACP的面积也就不难表示了.

二次函数习题课中,在笔者设计的问题链的引领下,使不同层次的学生都能突破自己的最近发展区,达到跳一跳就能摘到“桃子”的目的,更能驱动学生自主探究,使学生现有水平得到不断提升、不断发展.同时,既给基础薄弱的学生展示自我的机会,又给基础较好的同学提供探究的空间,达到提高课堂效率的目的.

层次化的问题设计可使每个学生都有动手、动脑、动口展示的机会和思考的个性化空间,让学生感受到数学知识的生长过程,引领学生深度学习,自主探究,提升学生核心素养.

教学有法,但无定法,贵在得法.数学课堂教学中,有目的、有计划的进行问题设计,既能调动学生的学习积极性,又能唤醒学生探究意识,引发学生思考,从而培养学生自主探究的能力和学生数学思维的灵活性、广阔性.