管土接触作用下直埋管道小折角优化分析

高 翔，王 飞，王国伟，雷勇刚

(太原理工大学 环境科学与工程学院，山西 太原 030024)

0 引 言

折角是供热直埋热水管道在施工过程中最易出现安全问题的管段，但因为施工躲避设计未见障碍物以及随高程敷设而改变方向，又不可避免.折角的不连续性会在其焊缝处出现应力集中，从而产生很高的局部峰值应力，导致管道局部破坏.

从国外研究学者Sobieszczanski[1]、A.M Gresnigt[2]等对单焊缝折角的研究，到近年来国内学者王飞[3]、杨辉[4]、李明强[5]、赵文浩[6]等人利用ANSYS软件对直埋管道的模拟研究，探究了折角的应力分布规律和最大Mises应力值.虽然至今已有较多利用有限元法对直埋管道分析的研究，但主要针对转角[7]、弯管[8-10]、椭圆度[11]等，极少数针对折角的研究也没有涉及到对供热直埋小折角管道进行结构优化，降低折角处的最大Mises应力，使其满足应力验算等方面要求.

本文基于非线性有限元分析方法，建立管土接触模型，探究用两个更小角度的折角代替一个小折角并加厚折角部分管道的优化结构是否能够使其最大Mises应力满足规范中对峰值应力[12]的验算要求，通过对比分析得到最优管件结构.

1 直埋管道有限元分析方法

1.1 材料模型

用双线性等向强化材料模型[8]描述供热管道的弹塑性特征，屈服准则采用Von Mises屈服准则[13].材料应力-应变关系如图 1 所示.管道材料使用Q235B钢材，材料参数如表 1 所示.

图 1管材应力应变曲线Fig.1 Tube stress strain curve

土体采用D-P模型[14]，该准则比较符合土壤的材料特性.Drucker-Prager屈服准则下屈服面不会因为材料逐渐屈服而改变，因此无相关强化准则，塑性行为可以被假定为理想弹塑性[8].同时，Drucker-Prager屈服准则也有效避免了屈服面在角棱处引起的奇异点.该屈服准则需要三个参数来定义：土壤粘聚力c，内摩擦角φ，膨胀角φf.

根据土壤的特性与实际情况，本文不考虑体积膨胀，故膨胀角φf=0.土体为靠近实际工程选取三七土，材料参数如表 2 所示.

表 1Q235B钢材材料参数值

表 2土体材料参数值

1.2 实体模型

根据埋地管道管土相互作用的特点，埋地时管道四周都会受到土壤对其的约束作用，本文将埋地管线与周围土壤综合考虑进行建模.直埋管道使用ANSYS软件提供的20节点的 SOLID95实体单元[15]进行模拟，该单元具有塑性、蠕变、应力刚化、大变形、大应变等特性，可以很好地适应曲线边界，并表达出折角处的应力集中状态.土壤使用六面体八节点的SOLID45结构实体单元进行模拟.将管土接触视为面-面接触，该接触方式支持有大滑动和有摩擦的大变形，协调刚度阵计算、不对称单元刚度阵的计算.管道的外表面为目标面，选择3D8节点的CONTA174单元；与管道接触的土壤表面为接触面，选择3D的TARGE170单元.

1.3 模型建立与边界条件

以自下而上的方式建立一个宽8 m，高4.5 m的长方体土壤模型和直管段长20m的埋地管道模型.管道上方覆土考虑到垂直动土压和垂直静土压的共同作用，选择1.5 m最为合适，也最符合施工中的实际情况.管道采用六面体扫略划分，网格大小为0.05 m，土体采用六面体映射划分，网格大小为1 m.

边界条件采用如下假定：土体上面为自由面，土体底面与管体两侧端面为全约束，土体其他面约束法向位移.对管道整体施加温度荷载，并在管道内壁施加压力荷载.

1.4 实验论证

本文以赵文浩[6]针对小折角的研究内容为基础，由于论文《管土接触作用下直埋供热管道折角的强度分析》中已对本文所采用的建模方法进行实验论证，本文不再赘述.

2 优化结构比较

2.1 小折角代替大折角的结构优化分析

为降低焊缝处应力集中水平，使其最大Mises应力值满足峰值应力的验算条件，满足强度要求，本文用两个更小角度的折角代替一个小折角进行建模，如图 2 所示.

图 2小折角代替大折角示意图Fig.2 Small fold angle instead of large angle

2.1.1 优化结构的建立

结构一：以厚度δ=10 mm的DN800管道为基础管径，埋深H=1.5 m，管道压力p=0.5 MPa，温度T=130 ℃，如图 3 所示.

图 3结构一管线双线图Fig.3 The structure one a pipeline of two-lines figure

结构二：在结构一的基础上，将一个a度折角管道变为有两个a/2度的折角管道，过渡段长L，如图 4 所示.

图 4结构二管线双线图Fig.4 The structure two a pipeline of two-lines figure

2.1.2 结构对比分析

以壁厚10 mm，过渡段长度L=2DN为基准参数，对DN800的管道进行建模，得出折角角度从1°～10°时焊缝内侧中心线处的最大Mises应力值进行分析比较，测点位置如图 5 所示，得出结论.

图 5结构一测点位置图Fig.5 Structure one of a measuring point locations

图 6结构二测点位置图Fig.6 Structure two of a measuring point locations

图 7结构一与结构二基于角度对比Fig.7 Structure one and structure two are based on angle contrast

通过图 7 的比较可以看出，结构一在管径DN800下，折角应力值在折角角度大于4°时有较大幅度的跃升，而结构二的最大Mises应力值变化幅度不大，只是随折角角度的增大，最大Mises应力值缓慢增加.说明结构二相比于结构一能有效降低管道小折角处的最大Mises应力值，即用小折角代替大折角的方法有效.

以管径DN800，壁厚10 mm为基准参数，分析5°与10°时结构一和结构二的应力分布图，如图 8，图 9 所示.

图 8结构一10°折角时的应力分布图Fig.8 The stress distribution figure of structure one at 10 ° angle

图 9结构二10°折角时的应力分布图Fig.9 The stress distribution figure of structure two at 10 ° Angle

从图8，图9的应力分布图中可以看出，随着角度的增加，最大Mises应力值向有折角的焊缝处集中，焊缝处变形越来越明显；同样，结构二中最大Mises应力值随着角度的增加也向有折角的焊缝处集中的趋势，但管道并未发生明显变形，并且焊缝处的应力集中程度也不如结构一明显.

从两种结构的应力分布图中可以看出，结构二在降低管道焊缝处应力集中程度，减小变形程度上均有明显优势.

2.2 中间段单侧加厚结构的优化分析

2.2.1 结构建立

结构三：在结构二的基础上，在管段L加厚Δδmm，如图 10～图 12 所示.

图 10结构三ANSYS建模图Fig.10 ANSYS modeling figure of structure three

图 11结构三剖面局部图Fig.11 A partial profile figure of the structure three

图 12结构三平面双线图Fig.12 Structure three plane two-lines figure

图 13结构三测点位置图Fig.13 Structure three of a measuring point locations

2.2.2 结构对比分析

以壁厚10 mm，加厚段长度L=2DN为基准参数，分别对DN800和DN1000的管道进行建模，得出折角角度从1°～10°时焊缝内侧中心线点处的最大Mises应力值并进行分析比较，得出结论.测点位置如图 14 所示.

图 14DN800 结构二与结构三基于角度对比Fig.14 DN800 Structure two and structure three are based on Angle contrast

从图14中可以看出，在管径DN800下，当折角角度在1°～5°时，结构二与结构三焊缝内侧中心线点处的最大Mises应力值均相差不大，且结构二的应力值相对更小，但折角角度大于5°之后，结构三焊缝内侧中心线点处的最大Mises应力值明显小于结构二，且随着角度的增大，焊缝内侧中心线点处的最大Mises应力值减小的程度越明显.

以管径DN800，壁厚10 mm，加厚段长度L=1DN为基准参数，分析5°与10°时结构二和结构三的应力分布图，如图 15，图 16 所示.

图 15结构二5°折角时的应力分布图Fig.15 The stress distribution figure of structure two at 5 ° angle

图 16结构三10°折角时的应力分布图Fig.16 The stress distribution figure of structure three at 10 ° angle

通过对比结构二与结构三在管径DN800下不同折角角度时最大Mises应力值的变化及其应力分布，可以发现加厚单侧管段壁厚可以有效降低折角角度大于5°的折角管段焊缝内侧中心线点处的最大Mises应力值，且结构三有效避免了改变角度的管段发生应力集中的现象.这说明加厚管段壁厚可以有效降低焊缝处的应力值，保护折角管段，避免其因应力集中而造成的局部破坏.

2.3 中间段双侧加厚结构的优化分析

2.3.1 结构建立

结构四：在结构三的基础上，在折角两端各加厚L/2长度的直管段，如图 17～图 19 所示.

图 17结构四ANSYS建模图Fig.17 ANSYS modeling figure of Structure four

图 18结构四剖面局部图Fig.18 A partial profile figure of the structure four

图 19结构四平面双线图Fig.19 Structure four plane two-lines figure

2.3.2 结构对比分析

分析结构三与结构四在管径DN800下分别改变折角角度a、加厚管段厚度Δδ和加厚管段长度L等不同条件下，得出分析结果.

1) 基于折角角度a的对比分析

以加厚段长度L=2DN，加厚厚度Δδ=3 mm为基准参数，对DN800的管道进行建模，得出折角角度从1°～10°时焊缝内侧中心线点处的最大Mises应力值并进行分析比较，得出结论.测点位置如图 20 所示.

图 20 结构四测点位置图Fig.20 Structure four of a measuring point locations

图 21DN800不同角度a下的应力值Fig.21 A stress value of DN800 under different angles

从图21中可以看出，随着折角角度a的增加，两种结构下DN800管道焊缝内侧中心线点处的最大Mises应力值会随之相应增长，但结构四对应角度处的应力值小于结构三，说明对焊缝两侧管段增加壁厚的方法比单侧加厚更能有效保护折角，避免焊缝处的局部破坏.

以管径DN800，加厚段长度L=2DN，加厚厚度Δδ=3 mm为基准参数，分析折角角度a为5°与10°时结构三和结构四的应力分布图，如图 22，图 23 所示.

图 22a=5°时结构三和结构四的应力分布Fig.22 The stress distribution figure of structure three and structure four when a=5°

图 23a=10°时结构三和结构四的应力分布Fig.23 The stress distribution figure of structure three and structure four when a=10°

从图 22，图 23 的应力分布图中可以看出，结构三①②段之间改变角度的最大Mises应力值转移到了结构四①②段之间改变壁厚的薄壁一侧，且因为加厚壁厚使管段因温度引起的热膨胀力增大，所以结构四相对结构三在某一角度下的最大Mises应力值分布范围更大.

2) 基于加厚段厚度Δδ的对比分析

以折角10°，加厚段长度L=2DN为基准参数，对DN800的管道进行建模，得出加厚厚度从2～7 mm时的最大Mises应力值进行分析比较，得出结论.

图 24DN800不同加厚厚度Δδ下的应力值Fig.24 A stress value of DN800 under different thickness degree Δδ

从模拟结果中可以看出，结构三中DN800管道的最大Mises应力值随加厚厚度Δδ的增加变化较小，稳定在275 MPa左右；结构四中DN800管道的最大Mises应力值随加厚厚度Δδ的增加而增大，到加厚厚度Δδ=5 mm之后逐渐趋于稳定.

以管径DN800，折角10°，加厚段长度L=2DN为基准参数，分析加厚厚度Δδ等于2 mm，7 mm时结构三和结构四的应力分布图.

选取结构三图12中③号管段具体分析其应力变化，如图 25～图 28 所示.

图 25Δδ=2 mm时结构三应力分布Fig.25 The stress distribution figure of structure three when Δδ=2 mm

图 26Δδ=7 mm时结构三应力分布Fig.26 The stress distribution figure of structure three when Δδ=7 mm

选取结构四图19中⑤号管段具体分析其应力变化，如下图所示.

图 27Δδ=2 mm时结构四应力分布Fig.27 The stress distribution figure of structure four when Δδ=2 mm

图 28 Δδ=7 mm时结构四应力分布Fig.28 The stress distribution figure of structure four when Δδ=7 mm

从图 25～图 28 结构三与结构四模拟结果中的应力分布情况可以看出，当增加壁厚时，最大Mises应力均出现在管道焊缝处薄壁的一侧，且由于焊缝处壁厚的变化程度增大而造成了管道最大Mises应力值的增加.

从应力分布图中可以看出，结构三最大Mises应力集中分布的范围随壁厚的增加而明显增大，结构四最大Mises应力集中分布的范围随壁厚的增加变化不大.

结构三与结构四的应力集中的位置都会从管道的焊接处向管道两侧偏移，但结构四应力集中位置从焊缝处向两侧偏移的效果更为明显，因而结构四相对结构三更能有效避免管道焊缝处因应力集中而造成的变形与破坏.

3) 基于加厚段长度L的对比分析

以10°折角，加厚厚度Δδ=3 mm为基准参数，对DN800管道进行建模，得出加厚段长度从1DN～3DN时的最大Mises应力值并进行分析比较，得出结论.

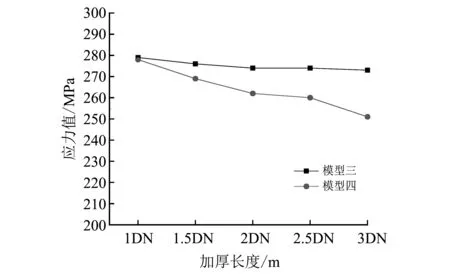
图 29DN800不同长度L下的应力值Fig.29 A stress value of DN800 under different length L

从图 29 中针对不同加厚段长度L的比较中可以看出，结构三最大Mises应力值随着加厚段长度L的增加会有较小幅度的减小，但总的来说变化幅度不大.结构四最大Mises应力值随着加厚长度L的增加明显逐渐减小，这说明增加加厚段长度对保护单焊缝折角，避免因应力集中而发生破坏是可以起到一定作用的.并且结构四比结构三降低最大Mises应力值的效果更为显著.

以管径DN800，折角10°，加厚厚度Δδ=3 mm为基准参数，分析加厚段长度L等于1DN，3DN时结构三和结构四的应力分布图.

从图 30，图 31 可以看出，相比于结构三，结构四中折角管件应力集中区域从改变角度处向改变厚度处转移，从而保护了管道改变角度的焊缝处因应力集中而造成的局部破坏.

图 30L=1DN时结构三和结构四的应力分布Fig.30 The stress distribution figure of structure three and structure four when L=1DN

图 31L=3DN时结构三和结构四的应力分布Fig.31 The stress distribution figure of structure three and structure four when L=3DN

3 结 论

由上述分析可得出一些结论：

1) 随着折角角度的增加，折角管段的最大Mises应力值会随之增长.但优化后的三种结构下最大Mises应力值均没有在某个角度处出现较大的跃升，直到10°其最大Mises应力值依旧能够满足峰值应力的验算条件，这为工程实践上大于5°的直埋小角度折角管道找到了可能的安装途径.

2) 用两个更小角度的小折角代替一小折角的方法在减小应力值，避免小角度折角管道焊缝处发生变形等方面十分有效，二个小折角之间管段长度不应小于2DN.

3) 当折角角度大于5°时，加厚局部管段壁厚的方法相比于仅用两个更小角度的小折角代替一个小折角的方法，更可以有效降低管段焊缝处的最大Mises应力值.

4) 三段加厚比单段加厚的方法更为有效.最大Mises应力值会随着厚度的增加而增加，但到5 mm之后，变化幅度减小，最大Mises应力值趋于稳定.考虑到工程投资，因此在工程应用中，将加厚厚度控制在5 mm之内是最优选择.同时，三段加厚长度L不小于3DN，应力最小.