覆冰塔线体系爆破除冰后的动力响应分析

曹咏弘，薛凯允，苗琳琳，李海涛，关学锋，张建军，李国平

(中北大学 理学院，山西 太原 030051)

0 引 言

中国是世界上输电线路覆冰最严重的国家之一，线路严重覆冰会造成倒塔、断线等事故，影响电网的安全运行，覆冰脱落则会引起电线脱冰跳跃，造成导线烧伤、跳闸等故障.

现有的除冰方法包括热力融冰法、机械除冰法、自然被动除冰法等，其中热力融冰法是目前使用较多的除冰方法，这类方法能耗较大，且只适用于覆冰厚度较小的情况，结合山西地区结冰频次相对较低，相关设施不完备，该方法不适合山西地区的除冰工作.采用预先敷设在输电线路上的线性装药爆破的方法[1]去除部分电线覆冰是近年来提出的一种成本低、见效快、效率高的除冰思路，该方法不仅可以保障电网全天候、全方式正常运行，更能精准控制脱冰位置和除冰长度，多相脱冰时，能够做到同步脱冰，具有很好的应用前景.

对于输电线路脱冰跳跃问题的非线性有限元数值模拟已开展很多.杜运兴等[2]研究了覆冰线路分层脱落时的动力响应，获得了两层覆冰不同时刻相继脱落引起的线路回弹高度、不平衡张力等；黄新波等[3]通过ANSYS建模得到了档距组合对导线脱冰跳跃的影响规律，并分析了脱冰时不平衡张力的影响因素[4]；张伟等[5]以实际运行输电线路的一耐张段为研究对象，重点分析了在相同脱冰率下，“全档脱冰”和“集中脱冰”两种脱冰方式对塔线体系脱冰响应的影响.

过去的研究中普遍将脱冰过程简化成档内均匀脱落，忽略局部脱冰的影响.本文结合爆破除冰方法，研究输电线路脱冰跳跃时，塔线体系在不同线型、脱冰档位置、档内脱冰位置(端部和中部)、脱冰率、导线脱冰顺序等不同工况下的动力学响应，得到保证体系安全的最大脱冰率和合适的脱冰方式.

1 塔线耦合系统有限元模型的建立

以某220 kV单回输电线路为研究对象，建立无高差等档距4塔5档塔线系统.采用L形梁建立与实际杆塔相一致的三维实体有限元几何模型，如图 1(a)和图 1(b) 所示，耐张段两端的转角耐张塔2B6-J1全高为27.5 m，呼称高度18.0 m；直线塔2B4-ZB1全高21 m，呼称高度18.0 m.

图 1塔线体系有限元模型Fig.1 Finite element models of tower-line system

导线和地线用梁单元建立并考虑阻尼影响赋予其阻尼系数[6]，相关设计参数见表 1.金具包括I型绝缘子串和耐张绝缘子串，其中I型绝缘子串为双联悬垂绝缘子串，长度为2 m；耐张绝缘子串形状为三角形，边长为0.4 m；绝缘子串的刚度相对较大，建模时可忽略其结构细节，简化为空间梁结构[7]，弹性模量和泊松比分别为207 GPa和0.3.塔线体系有限元模型如图 1(c) 所示.

表 1导线和地线材料及几何参数

2 爆破除冰数值模拟与分析

建立覆冰导线模型时，假设冰均匀地附着在导线表面.目前，输电线覆冰脱落的数值模拟方法包括：附加冰单元法[8]、改变密度法[9]和附加力模拟法[10].结合ABAQUS有限元软件的特点，本文采用改变密度法模拟未脱落部分覆冰的惯性作用，而覆冰脱落则通过改变惯性加速度来实现.

2.1 300 m多档输电线无冰和覆冰时的找形

针对山西易覆冰地区的常见覆冰厚度15 mm和30 mm，以一个耐张段4塔5档系统为例研究塔线系统无覆冰静载与覆冰静载响应，并对模拟结果和理论值进行对比.

图 2 给出了覆冰厚度为30 mm时，耐张塔与直线塔水平位移云图与应力分布云图，从图中可以看出耐张塔最大水平位移位于塔顶地线挂点处，而直线塔则位于塔顶导线挂点处；最大应力均位于两端导线的挂点处，由于直线塔的杆件在导线挂点处是由两根角钢拼接而成，故每根角钢只承担一半内力，如图2(d)所示，其大小为173 MPa.

图 2杆塔静载响应

由于耐张塔塔顶结构与挂点的不对称性，直线塔、耐张塔上横担处最外侧两端水平位移相反，这表示整个塔身产生小幅扭转变形，相对扭转位移即为塔左右两端沿导线方向水平位移之差.塔身应力分布、相对扭转位移、最大水平位移与覆冰厚度的关系，如表 2 所示.

表 2耐张塔与直线塔在不同载荷下位移与最大应力对比

从模拟结果可知，导线和地线在自重作用下呈现平抛物线悬挂状态，导线中部弧垂最大，大约为5.694 m，理论计算值为5.534 m，两者误差约为2.9%，说明数值模拟方法正确可行.

2.2 300 m多档输电线导地线脱冰时的动力响应

以一个耐张段4塔5档模型为例，分析导地线脱冰时的动力响应，覆冰厚度30 mm，双分裂导线初始间距为400 mm，脱冰过程中导线发生跳跃，相间距离产生变化，为防止除冰时子导线碰撞，做如下偏于安全的假定：分裂导线子导线间距在导线舞动过程中应不小于100 mm.由模拟结果可得到导地线中点位移、杆塔两侧导地线挂点处应力差，即相邻档张力差，选取双分裂导线舞动过程中的相间距离、相邻档张力差和直线塔横向位移作为安全考察标准.

图 3脱冰方式、导地线挂点及档位示意图Fig.3 The diagram of ice-shedding pattern, wire suspending points and spans

直线塔导线与地线挂点示意图如图 3 所示，A1、A2，B1、B2，C1、C2为双分裂导线，D1、D2为地线.

2.2.1 地线脱冰时塔线耦合体系的动力响应

1) 单根地线脱冰动力响应

图 4 分别对比了第二档单根地线在不同脱冰方式及脱冰率下，脱冰档地线冰跳高度、相邻档间张力差及直线塔塔顶地线挂点处最大水平位移随脱冰率的变化.

图 4单根地线不同脱冰率下的动力响应Fig.4 Dynamic responses under different de-icing rates of single ground wire

可以看出，随着脱冰率的增加，这三个变量呈非线性增长趋势，端部脱冰时各项参数都要低于中部脱冰方式，当脱冰率较小时，端部脱冰相对更加安全.考虑到地线与导线初始间距约为4.6 m，为防止冰跳过程中导线和地线发生碰撞，应采用端部脱冰方式，脱冰率小于30%.

2) 双地线同时脱冰动力响应

从上节分析可知，单根地线从端部脱冰时更安全.

图 5双地线不同脱冰率下的动力响应Fig.5 Dynamic responses under different de-icing rates of double wires

针对双地线同时脱冰，选择端部同步脱冰方式，分析不同脱冰率下脱冰档地线的舞动情况及塔身位移和相邻档间张力差，如图 5 所示.

随着脱冰率的增加，从图5(a)可以看出，脱冰档舞动幅度明显增加，幅值与上节单根地线脱冰非常接近；由图5(b)看出，脱冰档与其邻档地线挂点处张力差逐渐增大，当整档全部脱冰时，最大张力差约为190 MPa，与单根脱冰一致；由图5(c)、(d)看出，挂点水平位移明显增加，单根脱冰与双根同时脱冰两种脱冰方式下挂点水平位移差值也有所增加，脱冰率为100%时增加约10 mm.因此，双根地线同时脱冰时脱冰率应控制在30%以下.

2.2.2 导线脱冰时塔线耦合体系的动力响应

双分裂导线子导线间初始间距为δ0=400 mm，假设双分裂上方、下方导线在脱冰过程中的挠度分别为w1(t),w2(t)，可得到脱冰过程中两子导线相间距离，即弧垂差Δ的时间函数为

Δ=δ0+w1(t)-w2(t).

(1)

如前所述，当双分裂导线在舞动过程中间距太小时会造成危险，以间距100 mm为临界值，即当Δ<100 mm时是危险的.

1) 单导线脱冰动力响应

图 6 给出了二档B1线中部和端部脱冰时，脱冰档及其邻档双分裂导线舞动弧垂差的时程曲线；从图6(a)可以看出，二档B1中部脱冰10%时，脱冰档分裂导线相间距离满足安全要求，但邻档双分裂导线舞动时存在相互碰撞的危险，由于脱冰率越高导线舞动越强烈，故B1单导线中部脱冰率大于10%的方案不可行.由图6(b), (c)看出，二档B1端部脱冰时，脱冰率在20%之内导线舞动幅值满足要求，当脱冰率为30%时，邻档导线舞动超过临界值.因此，对于单根导线脱冰，应采用端部脱冰的方式，且初始脱冰率不大于20%.

2) 双分裂导线同时脱冰动力响应

图 7 给出了第二档双分裂导线B1、B2中部和端部脱冰时，脱冰档与其邻档导线舞动弧垂差的时程曲线.从图7(a)可以看出，对于双分裂导线B1、B2中部同步脱冰，当脱冰率增加至20%时，脱冰档导线舞动达到临界值，因此对于双分裂导线中部同时脱冰，初始脱冰率应不大于10%.由图7(b)、(c)看出，对于导线B1、B2端部同步脱冰，脱冰率小于30%时，脱冰档及其邻档导线舞动都在临界值之内，符合要求，当脱冰率为30%时，邻档导线相间距离逼近临界值，故双分裂导线端部同时脱冰的初始脱冰率应不大于30%.

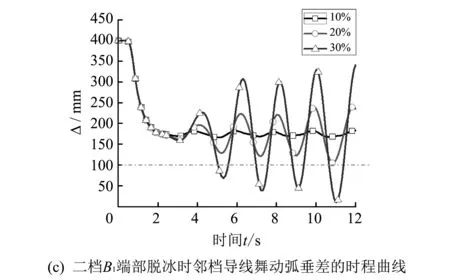
图 6单导线脱冰时导线舞动弧垂差的时程曲线Fig.6 Time curves of sag difference of conductors galloping after ice shedding of single conductor

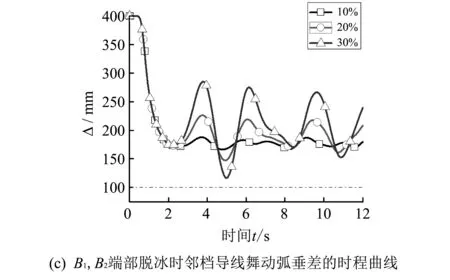
图 7第二档双分裂导线脱冰时导线舞动弧垂差时程曲线Fig.7 Time curves of sag difference of conductors galloping after ice shedding of secone double bundled conductors

2.2.3 分步式脱冰动力响应分析及安全性检验

1) 第二档B线脱冰全过程安全性分析，本节计算模型中第二档地线均无覆冰，其他导线和地线均有覆冰.方案如下：第一步：对第二档B线一端脱冰30%，其分析过程见2.2.2节内容；第二步：对第二档B线另一端脱冰方案选择，如图 8(a) 所示，脱冰率为20%时，导线舞动相间距离大于100 mm，两种脱冰方式下导线挂点两端张力差均在3～4 MPa之间，符合安全要求.第三步：对第二档B线第三次脱冰方案选择，选择与第一步初始脱冰相同的位置，如图8(b)所示，当脱冰率为5%时满足安全要求.第三步之后的脱冰率可根据实际情况逐渐递减.

2)第二档A或C线脱冰全过程安全性分析，按照上一节的方案将第二档B线的冰完全除去之后，可对A或C线进行除冰作业.拟采用与B线相同的方式脱冰，经分析当按照B线脱冰方式对A线或C线脱冰时，其舞动幅值满足要求.但同时发现，无覆冰的B线，舞动与挂冰时相差较大，容易发生碰撞，经模拟计算，当在B线上增加临时间隔棒后可以有效增大双分裂B线间距，避免其在舞动过程中相互碰撞.所以，在第二档B线完全脱冰后，需要增加临时间隔棒，然后再对A或C导线进行脱冰.

3)第一档B导线脱冰全过程安全性分析，由于第一档位于耐张塔与直线塔之间，连接导线挂点存在一定的高程差，舞动规律与第二档略有差别，通过模拟分析，存在高程差的导线脱冰时应按以下步骤：第一步脱冰20%，第二步脱冰5%，第三步脱冰5%.

4)第一档A或C导线脱冰全过程安全性分析，经模拟之前所确定的方法在第一档仍然适用.

图 8第二档B线分步脱冰方案选择Fig.8 The selection of step-by-step de-icing scheme of second stall B line

3 结 论

通过对塔线耦合体系有限元模型的分析，计算了自然状态、覆冰状态及不同脱冰方式下结构的力学响应特性，导线和地线覆冰30 mm时，对爆破除冰过程中塔身应力、导地线弧垂及其舞动情况进行了对比分析，提出了档距为300 m时的脱冰方案.

1) 单根导线和地线单次脱冰方案：需从中间档开始脱冰；采用端部脱冰方式；地线初始脱冰率小于30%；导线初始脱冰率小于20%.

2) 双分裂导线同时脱冰方案：双分裂导线中部同时脱冰时，脱冰率不大于10%；端部同时脱冰时，初始脱冰率不大于30%.

3) 同档内分步脱冰方案：为防止已除冰的导线发生碰撞，在线路正常运行情况下需对已除冰的导线增加临时间隔棒，分步式脱冰率要逐级降低，存在高程差的导线脱冰时要适当减小脱冰率.

4) 当线路可断电脱冰时，不考虑导线相互碰撞，可采用100%完全脱冰，导线和地线及塔身应力均可满足强度要求.单次单根脱冰时，结构上应采用对称脱冰顺序，防止产生过大档间张力差.