电动负载模拟器加载系统动态特性分析

刘伟良，杨瑞峰，郭晨霞，葛双超

(1.中北大学 仪器与电子学院，山西 太原 030051；2.山西省自动化检测装备与系统工程技术研究中心，山西 太原 030051)

0 引 言

负载模拟器是模拟飞行器舵机在实际飞行的过程中所受到的空气铰链力矩，测试舵机性能的重要设备[1-3].由于电动负载模拟器具有加载精度高、稳定性较好、易操作、易维护等优点，目前得到广泛应用[4-10].

电动负载模拟器是电机发出扭矩，通过加载系统对舵机进行扭矩加载，达到模拟舵机在空气中所受到的铰链力矩的目的.其加载系统直接影响电动负载模拟器的加载性能，所以有必要了解其动态特性.目前，研究者们对电动负载模拟器的研究已经取得很大的成就，比如于杰等设计了双单机的负载模拟器来提高加载性能[11]；陈家新等以永磁同步电机为加载电机建立了负载模拟器的数学模型并分析其性能[12]；雷建杰等对影响电动负载模拟器性能的因素做了分析[13]；唐英博提出一种三闭环控制结构来提高加载精度[14].但迄今为止很少有对加载系统动态特性进行分析的相关文献，所以为了解其系统的动态特性，本文通过Solid work建立系统的3D模型，并导入ANSYS Workbench中进行模态分析，分析了其前6阶模态的固有频率和振型；通过MATLAB软件建立系统的数学模型，改变系统中弹簧杆的刚度，研究弹簧杆刚度对系统的影响，为未来电动负载模拟器的设计和优化提供理论依据.

1 有限元模型的建立

电动负载模拟器加载系统的结构图如图 1 所示.

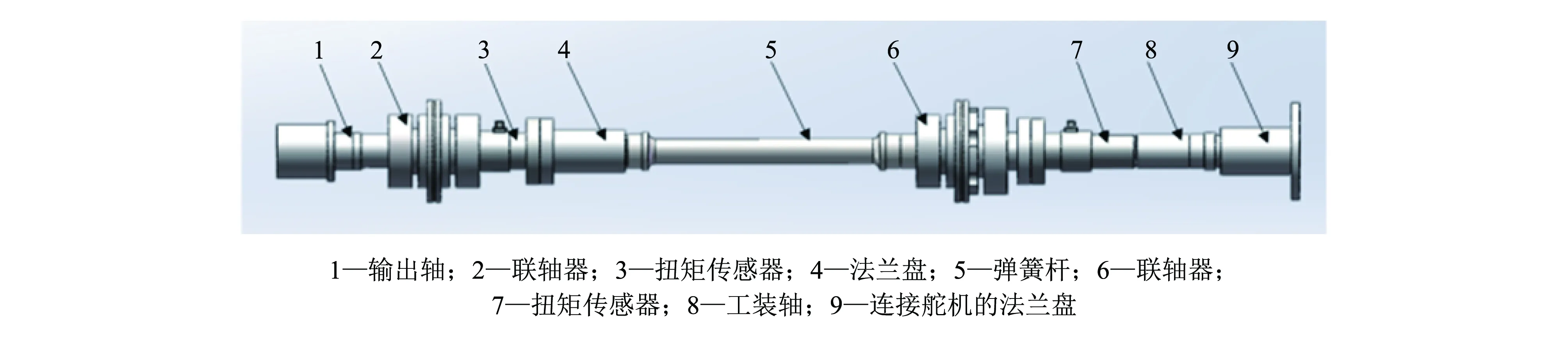
图 1加载系统结构图Fig.1 Loading system structure

建立电动负载模拟器加载系统的3D模型后，将模型导入ANSYS Workbench中进行网格的划分.对模型进行网格划分的时候，考虑到复杂的系统机构对网格质量和后期计算的影响，所以为了保证网格划分的质量，需要忽略不影响分析结果的圆角、倒角、螺纹等微小结构[15].采用Solid187单元进行网格划分，共产生187 475个单元，320 576个节点，系统网格划分如图 2 所示.

图 2加载系统有限元模型Fig.2 Loading system finite element model

2 模态分析

2.1 材料属性及边界条件

对系统进行模态分析之前需知道各个零件的属性，其弹簧杆的材料为40Cr，扭矩传感器材料为30CrMnSiA，联轴器分别由2个法兰连接盘和2个法兰盘中间的板弹簧组成，其中法兰盘材料为S45C，板弹簧材料为SUS304，其它材料为 45#钢.各零件的相应属性见表 1.

表 1材料属性

由于加载系统的输出轴和第一个扭矩传感器通过联轴器连接在一起；第一个扭矩传感器通过螺栓和法兰盘连接；弹簧杆通过键和法兰盘连接在一起；弹簧杆与第二个扭矩传感器通过联轴器连接在一起；第二个扭矩传感器和工装轴通过键连接在一起；工装轴和连接舵机的法兰盘也是通过键连接在一起，零件之间几乎没有相对位移，所以零件面与面之间的接触方式设置为绑定(Bonded).整个系统是通过深沟球轴承支撑，根据文献[16]得到这类轴承的特性，在轴上相对应的位置设置轴承约束，与舵机连接的部分设置为固定约束.

2.2 模态求解及分析

模态分析的方法有很多种，本文采用的是Block Lanczos法.Block Lanczos法是用矢量进行递归计算，与其它方法相比具有运算速度快、结构精确等优点.根据文献[17]得知高阶固有频率对系统动态特性分析意义不大，所以本文只提取系统的前6阶模态频率，其频率见表 2，振型如图 3 所示.

表 2前6阶模态频率

图 3前6阶振型图Fig.3 First six mode

由模态分析的结果可以得到前6阶模态振型分别为：1和2阶模态为绕Z轴的扭转振型，1阶模态中系统前端部分的联轴器连接部分变形量最大，2阶模态中系统后端部分的联轴器连接部分变形量最大；3阶模态主要是弹簧杆到后端扭矩传感器连接部分绕Z轴的摆动振型，其中联轴器部分变形量最大；4阶模态是绕Z轴的摆动振型，联轴器后半部分和扭矩传感器部分变形量最大；5阶模态主要是系统前端到弹簧杆部分绕Z轴的摆动振型，以前端联轴器和扭矩传感器连接部分为界限，两边的摆动方向相反，弹簧杆前端部分变形量最大；6阶模态是系统弹簧杆到后端部分绕Z轴的摆动振型，以后端联轴器连接部分为界限，两边的摆动方向相反，弹簧杆中间部分变形量最大.

通过对加载系统前6阶模态振型分析可知，振型主要是系统的绕Z轴的扭转振型和摆动振型，幅值最大部分主要是两个联轴器和弹簧杆.

3 弹簧杆对系统的影响

3.1 包含弹簧杆刚度的系统数学模型

弹簧杆是系统中重要组成部分，直接影响整个系统加载性能.为了更好地了解弹簧杆对系统的影响，通过MATLAB建立包含弹簧杆刚度的数学模型如图 4 所示.

图 4包含弹簧杆刚度的数学模型Fig.4 Mathematical model containing the stiffness of the elastic rod

图 4 中：Um为电枢电压；Lm为电机电感；Rm为电机电阻；im为电路中的电流；Tm=Kmim为电机输出扭矩；Km为转矩系数；ω为角速度；Ke为反电动势系数；TL为负载扭矩；J为转动惯量；θm为加载后系统的转角；θf为舵机的转角；G为弹簧杆刚度.

根据数学模型得到其传递函数为

TL=G(KmUm-G1(s)θf)/G2(s),

(1)

其中

G1(s)=JmLms3+JmRms2+KmKes,

G2(s)=JmLms3+JmRms2+

(KmKe+LmG)s+GRm.

3.2 弹簧杆对多余力矩的影响

当系统输入零信号时，舵机输出的力矩即为多余力矩，它会严重影响对舵机的加载性能，如带宽变窄、稳定性变差、跟踪精度降低等[17]，所以需要抑制多余力矩来提高电动负载模拟器的加载性能.根据图4可以得到关于多余力矩的传递函数为

(2)

实际测试中，会更换不同刚度的弹簧杆达到改变系统结构刚度的目的，以满足对不同舵机的测试要求.为了更好地了解弹簧杆对多余力矩的影响，现在设置弹簧杆刚度为初始刚度的1/10, 1/2, 5倍，10倍，得到与多余力矩的关系如图 5 所示.

从图 5 中得到，在低频段10 rad/s内，不同刚度情况下的幅频特性曲线基本重合在一起，所以在低频段弹簧杆刚度的变化对多余力矩的幅值影响相对较小.但是在10 rad/s以后的中高频段，刚度的变化对多余力矩有很大的影响；当刚度为0.1倍的时候，幅频特性的值为46 dB左右，随着弹簧杆刚度增大，多余力矩幅值会大幅度地增大，当弹簧杆刚度为10倍的时候，幅频特性的值高达89 dB.相位是随着弹簧杆刚度的增大越来越超前；频率在150 rad/s以内的时候，当弹簧杆刚度很小为0.1倍的时候，相位就会超前90°，同时在弹簧杆刚度为10倍的时候，相位超前会达到162°.所以，在设计过程中应合理设置弹簧杆刚度来抑制多余力矩对系统的影响.

图 5多余力矩和弹簧杆刚度的关系Fig.5 Relationship between excess torque and spring rod stiffness

3.3 弹簧杆对系统的影响

同样条件下设置弹簧杆刚度为初始刚度的1/10, 1/5, 1/2, 2倍, 5倍, 10倍，得到系统前6阶模态频率见表 2，固有频率和弹簧杆刚度的关系如图 6 所示，系统的幅频特性如图 7 所示.

表 3不同弹簧杆刚度的模态频率

图 6系统固有频率随弹簧杆刚度变化规律Fig.6 The natural frequency of the system changes with the stiffness of the elastic rod

图 7不同刚度下的幅频特性图Fig.7 Amplitude-frequency characteristic diagram on different stiffness

从表 2, 图 6 可以得到，弹簧杆刚度从0.1倍增到10倍的时候，系统的1阶模态频率由84 Hz增加到214 Hz，2阶模态频率由282 Hz增加到501 Hz，3阶模态频率由377 Hz增加到609 Hz，4阶模态频率由438 Hz增加到761 Hz，5阶模态频率由628 Hz增加到949 Hz，6阶模态频率由778 Hz增加到1 463 Hz；所以随着弹簧杆刚度的增大，会使整个系统结构刚度变大，同时系统的固有频率也随着变大.

通过图 7 幅频特性图可以得到不同弹性杆刚度下的截止频率，当刚度为0.1倍的时候截止频率为13.1 Hz，0.2倍为13.4 Hz，0.5倍为13.9 Hz，1倍为14.7 Hz，2倍为18.1 Hz，5倍为23.9 Hz，10倍为31.3 Hz.因为截止频率和系统带宽频率成正比，截止频率越大系统带宽频率也越大，系统响应的速度也越快；所以随着弹性杆刚度变大，截至频率逐渐变大，系统带宽频率也变大，系统响应速度变快.但是随着弹簧杆刚度的增加，幅频特性图中出现机械谐振，这是因为刚度变大，带宽变宽以后系统的固有频率会出现在带宽的范围内，当外界激励频率达到系统的固有频率的时候，就会引起机械谐振，影响系统稳定性，破环系统机械结构；同时从图 7 得到，当弹簧杆刚度为1倍的时候，谐振峰值为17.7 dB，2倍为23.8 dB，5倍为30.2 dB，10倍为38.4 dB，所以随着刚度的变大，机械谐振的峰值也随之变大.因此，在设计电动负载模拟器加载系统的弹簧杆的时候，要根据测试要求来设计弹簧杆，不仅需要系统具有良好的响应速度，同时还要避免机械谐振的出现.

3.4 仿真分析

用三组弹簧杆刚度为300 N·m/rad, 550 N·m/rad, 800 N·m/rad得到的系统仿真如图 8～图 10 所示.仿真实验中，其加载的扭矩值为20 N·m，频率为1 Hz.

图 8300 N·m/rad系统响应曲线Fig.8 The system response curve of 300 N·m/rad

图 9550 N·m/rad系统响应曲线Fig.9 The system response curve of 550 N·m/rad

图 10800 N·m/rad系统响应曲线Fig.10 The system response curve of 800 N·m/rad

从图 8～图 10 中可以得到，当弹簧杆刚度为300 N·m/rad的时候，加载后曲线的峰值为19.8 N·m，曲线响应时间滞后0.13 s；刚度为500 N·m/rad的时候峰值为19.4 N·m，滞后0.09 s；刚度为800 N·m/rad的时候峰值为18.6 N·m，滞后0.02 s.随着刚度的增加，加载后曲线峰值会降低，这是因为当弹簧杆刚度大的时候，多余力矩影响较大，所以加载后的曲线峰值低.当弹簧杆刚度低的时候，整个系统的响应速度会变慢，所以刚度为300 N·m/rad的时候，系统响应时间滞后最多.为了使系统加载后的曲线能较好地复现，且响应速度较快，经大量仿真实验得到，当弹簧杆刚度低于500 N·m/rad的时候，系统响应时间滞后接近0.1 s，响应速度太慢；当弹簧杆刚度高于600 N·m/rad，加载后曲线的峰值太低，多余力矩的影响较大.所以电动负载模拟器加载系统中弹簧杆刚度设计最佳范围为500～600 N·m/rad，这个时候系统的稳定性好，响应速度快，系统不会发生机械谐振，且多余力矩干扰相对较小.

4 结 论

1) 建立了电动负载模拟器加载系统的有限元模型，对系统进行了模态分析，得到系统前6阶模态频率和相应的振型.

2) 通过改变弹簧杆刚度，得到随着弹簧杆刚度的变大，固有频率也变大，系统带宽变宽，系统响应速度变快，但是会造成机械谐振，破坏整个系统的稳定性，且随着刚度变大，谐振峰值随之增大，多余力矩也会变大.通过仿真实验得到弹簧杆刚度设计的最佳范围是500～600 N·m/rad.

3) 通过分析系统的模态特性和弹簧杆刚度对其的影响，可以很好地了解电动负载模拟器加载系统的动态特性，为未来设计和优化提供了理论依据.