BOC信号自相关函数边峰消除方法改进和性能分析
张 鹏,张胜男,王存宝,李孟委,3,张晓峰,李维刚
(1.中北大学 仪器与电子学院,山西 太原 030051;2.山西北方机械制造有限责任公司,山西 太原 030009;3.中北大学 电子测试技术国家重点实验室,山西 太原 030051)
0 引 言
随着全球卫星导航系统、区域导航系统以及增强导航系统的不断发展,卫星数量越来越多,但是频带资源有限,根据国际电信联盟的规定目前采取“先用先得”的规则,所以如何解决频段资源紧张问题成为了研究热点[1-3].全球卫星导航系统最初采用的调制方式为二进制相移键控(Binary Phase Shift Keying,BPSK),但是这种调制方式不能解决频带拥挤的问题[4].随着导航技术的发展,二进制偏移载波(Binary Offset Carrier, BOC)作为一种新型的调制方式被用来解决上述问题,这是因为一方面可以很好地在实现频段共用的同时保证频谱分离,提高频谱的利用率;另一方面,在相同的码速率下,BOC调制的相关函数比BPSK调制的相关函数更陡峭,性能更优[5-6].我国北斗系统现已采用BOC调制方式.
但是因为BOC调制信号的自相关函数具有多峰的特点,并且随着BOC信号调制阶数的增大,边峰距离主峰的距离越近,幅值也越大.当受到噪声干扰时,边峰位置处的相关结果极有可能超越主峰位置,从而使系统判定相关结果最大值发生在边峰位置,错误地将边峰当作主峰,判定信号捕获成功.这种误捕获就是在BOC信号捕获过程中需要解决的模糊问题.为解决这种捕获模糊性,基本方法有自相关边峰对消法(auto-correlation side-peak cancellation technique,ASPcCT)、副载波相位消除法(SCPC)、BPSK-like法、相关函数分型重构法、伪相关函数法(PCF)、主瓣叠加法等[7].
ASPcCT虽然应用广泛,但是也仅适用于SinBOC(n,n)信号;SCPC适用于任意阶数的正余弦BOC信号;BPSK-like法和主瓣叠加法实现简单,但是硬件设计复杂;PCF适用于偶数阶的正弦BOC信号;相关函数分型重构法适用于高阶BOC信号[8-11].本文针对自相关边峰对消法(ASPeCT)仅适用于SinBOC(n,n)信号,适用面窄,信号处理过程需要用到BOC信号的自相关函数和互相关函数,计算量较大的缺点,提出了一种改进的北斗微弱信号捕获方法.
1 自相关边峰消除法(ASPcCT)
ASPcCT通过将SinBOC(n,n)信号的自相关函数与互相关函数进行平方作差,就可以消除边峰,从而得到单一的自相关峰值.SinBOC(n,n)信号的自相关函数为

(1)
SinBOC(n,n)信号的互相关函数为:
RPRN-BOC(n,n)=

(2)
则ASPeCT的表达式为
(3)
以BOC(1,1)为例,其自相关函数为

(4)
BOC(1,1)和本地伪码的互相关函数为
(5)
式中:τ为码片的延迟数目;tri()为三角函数.从而可得ASPeCT算法表达式为
(6)

图 1ASPeCT算法曲线Fig.1 ASPeCT algorithm curve
由式(6)可得ASPeCT算法自相关仿真曲线(图 1),ASPeCT算法虽然消除了BOC(1,1)信号自相关函数的两个边峰,但是又出现了两个负峰.在实际卫星信号捕获过程中,受前端滤波的影响,SinBOC(n,n)信号的自相关函数的相关峰会出现移位和形变.所以为了消除前端滤波的影响,可使用参数β对其进行修正,式(3)可改写为
(7)
2 改进的边峰消除技术
根据SinBOC(n,n)信号的自相关函数与互相关函数的表达式,有如下关系
(8)
由式(8)可知,SinBOC(n,n)信号的自相关函数与互相关函数的绝对值相加,也可以消除边峰,获得单一的峰值信号.
由于ASPcCT算法仅适用于SinBOC(n,n)信号,因此根据式(1)所示SinBOC(n,n)信号的自相关函数表达式,有CosBOC(n,n)信号的自相关函数表达式为

(9)

图 2SinBOC(n,n)与CosBOC(n,n)自相关曲线Fig.2 The autocorrelation curve of SinBOC(n,n) and CosBOC(n,n)
对SinBOC(n,n)信号和CosBOC(n,n)的自相关函数进行仿真,由此可得到如图 2 所示的自相关函数曲线,CosBOC(n,n)自相关曲线比SinBOC(n,n)自相关曲线多了两个小的正边峰.
x+|x|=0(x<0).
(10)
为消除CosBOC(n,n)自相关曲线上的两个小的正边峰,由式(6)和式(9),构造函数式为
R2(τ)=RCos BOC(τ)-α|RBOC/PRN(τ)|+
|RCos BOC(τ)-α|RBPC/PRN(τ)||.
(11)
当采用恰当的α值时,就可以将式(11)中RCosBOC(τ)-α|RBOC/PRN(τ)|的负峰消除,相关函数只有一个主峰.由此可知改进后的ASPeCT算法可以适用于任意阶数的正余弦BOC信号.针对ASPeCT算法需要用到BOC信号的自相关函数和互相关函数,为了进一步降低运算量,加快北斗信号捕获速度,对式(10)进一步改进,令
R3(τ)=RBOC(n,n)(τ)+|RBOC(n,n)(τ)|.
(12)
从而有
|RBOC(n,n)(τ)-α|RBOC/PRN(τ)||≤|RBOC(n,n)(τ)-
x+|x-α|RBOC/PRN(τ)||.
(13)
当x=0时,由式(11)和式(13)有
RLong(τ)=RBOC(n,n)(τ)-α|RBOC/PRN(τ)|+
|RBOC(n,n)(τ)-α|RBOC/PRN(τ)||≤
RBOC(τ)-α|RBOC/PRN(τ)|+|RBOC(τ)|+
|α|RBOC/PRN(τ)||≤RBOC(n,n)(τ)+
|RBOC(n,n)(τ)|=R3(τ).
(14)
由此可知,当取恰当的α值,应用改进后的构造函数式,只需要使用BOC信号的自相关函数就可以消除自相关函数的边峰.
3 算法性能分析
采用BOC(6,1)调制方式的北斗卫星信号来对改进后的边峰消除算法进行捕获性能分析,该调制方式的偏移载波频率为fsc=6.138 MHz,信号采样频率为2fsc=12.276 MHz.根据构造的函数设计了伪码捕获测试环路,如图 3 所示.

图 3伪码捕获测试环路Fig.3 Pseudo-code capture test loop
通过对本地副载波的移相处理,可以使得伪码为最大值时的BOC(n,n)与接收到的亚载波同相,此时有唯一的伪码相位.在伪码捕获测试环路中,本地构造的自相关函数为SinBOC(n,n),环路中加入了信噪比为-20 dB的高斯白噪声,捕获时间为1 ms.
图 4(a) 为BOC(6,1)调制下直接捕获伪码相位的曲线图,图 4(b) 为采用所构造的函数捕获伪码相位的曲线图,图4(c), 图4(d)分别为图4(a),图4(b)峰值处的局部放大图.图 5 为BOC(6,1)调制方式下采用直接捕获伪码相位和采用所构造的函数捕获伪码相位的主峰和边峰的比值.

图 4BOC(6,1)调制下直接捕获和采用构造的函数进行捕获的捕获曲线Fig.4 Capture curves captured directly by BOC (6,1) and constructed by functions
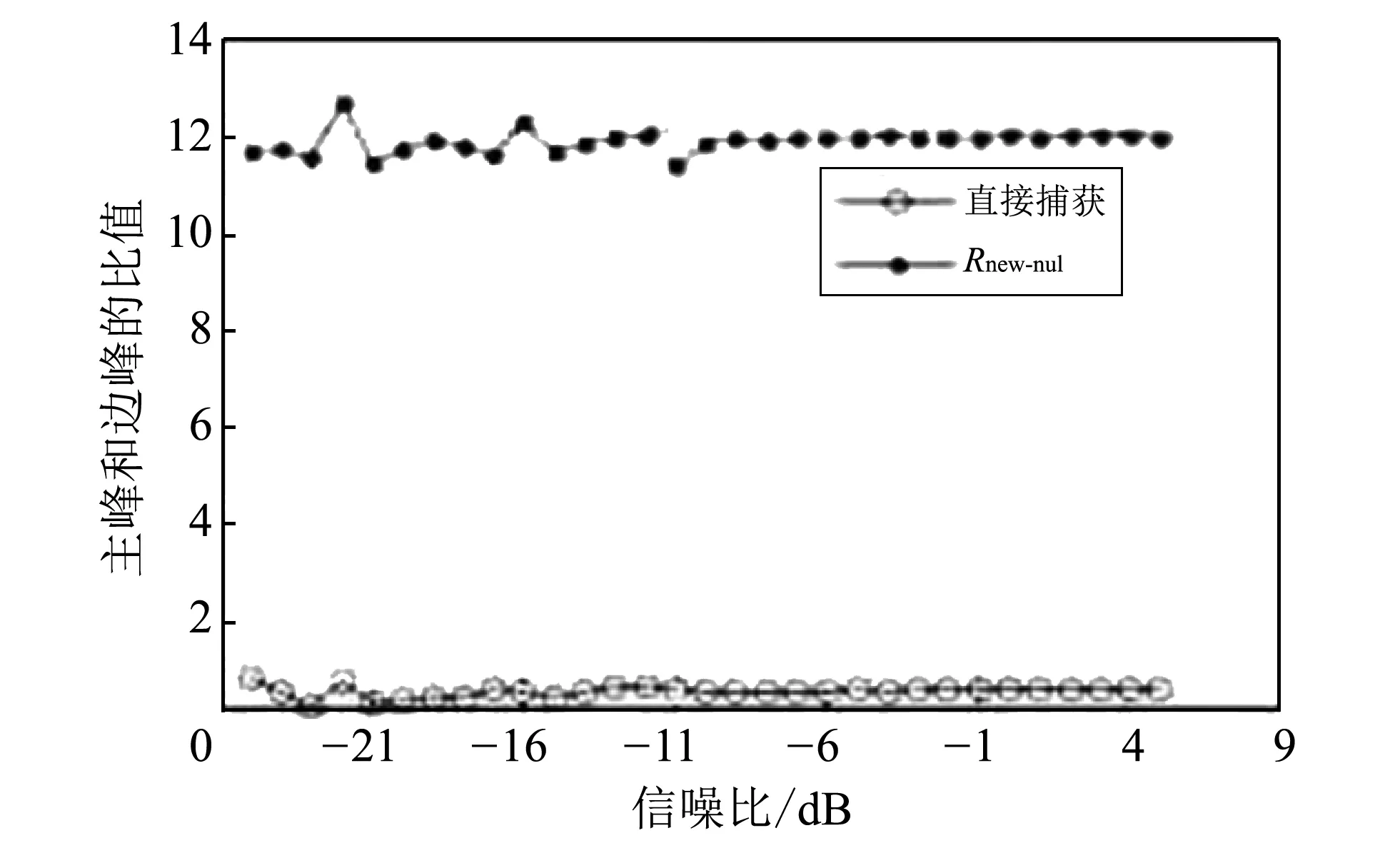
图 5主峰和边峰的比值Fig.5 The ratio of the main peak to the edge peak
由图 5 可知,采用所构造的函数捕获伪码相位的主峰和边峰的比值明显高于采用直接捕获伪码相位的主峰和边峰的比值,其值由1 dB提升至12 dB,验证了所构造的函数的有效性.分析和实验结果表明,改进后的算法适用于任意阶正余弦BOC(n,n)信号,并且只需要使用调制信号的自相关函数就可以完成负边峰消除,运算量低,主峰和边峰的比值显著提高,更容易准确捕获北斗微弱信号.
4 结 论
针对北斗BOC调制信号自相关函数的多峰性对信号捕获带来模糊影响,并且ASPcCT算法仅适用于SinBOC(n,n)信号的问题,本文对ASPeCT算法流程和捕获效果进行了研究,对其应用加以拓展和改进,在适用于任意阶正余弦BOC(n,n)信号的基础上,进一步降低运算量,只需要自相关函数就可以完成边峰消除.通过使用BOC(6,1)调制方式的北斗卫星信号对改进后的算法进行性能分析可知,自相关幅值更高,捕获效果更好,BOC调制信号的无模糊捕获性能更优.

