基于重采样技术的短码直扩信号伪码估计

，，

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

直接序列扩频(Direct Sequence Spread Spectrum，DSSS)通信具有优异的抗干扰能力、多址能力、保密和抗多径性能，因而被广泛地应用于无人机遥控、卫星导航和3G蜂窝手机等军事和民用通信系统中。短码直接序列扩频是用一个周期伪码序列(Pseudo Noise Code，PN Code)去调制一个信息码元，是目前应用较为广泛和研究较多的直扩体制[1]。

在通信对抗行动中，通信侦察方期望获得敌方直扩通信的扩频伪码序列，进而解扩得到信息序列。然而作为非合作方所能获得的有关通信协议十分有限，因此如何利用有限的先验知识快速而准确地从截获信号中估计扩频伪码序列就是极为重要和迫切需要解决的。

目前常见的短码直扩信号的伪码估计方法有神经网络方法[2]、时域相关检测方法[3-4]、矩阵特征分解方法[5-7]等。这些方法要求先以整数倍码元速率的采样率对空中信号进行采样，然后从采样信号解调得到基带0/1伪码采样序列，再按一定间隔从中提取出扩频伪码。然而非合作方侦收到的信号一般质量较差，直接从空中采样信号解调基带0/1序列会有较大误码，给扩频伪码估计的准确性带来很大影响；另一方面，实际中侦察获取采样信号时，采样设备所能提供的采样率难以与直扩信号码元速率成整数倍关系，使得每个码元上的采样点数不相一致，提取扩频伪码时的抽样判决点的正确选择变得十分困难，方法估计性能大为下降，鲁棒性难以得到满足，距离实际的工程应用还有较大差距。

本文针对上述估计方法存在的问题，提出了基于重采样技术的短码直扩信号伪码估计方法。该方法能够克服非整数倍码元速率的采样率情况下伪码估计时抽样判决点选取的不确定性，实验验证了方法的有效性和可靠性。

1 基本理论

1.1 信号模型

图1所示为短码直扩信号的发射和接收处理模型[1]。

假设扩频信号通过加性高斯白噪声信道，接收机收到信号经过混频滤波，得到中频信号[8]：

r(t)=d(t)p(t)cosω0t+n(t)

(1)

以采样率fs对r(t)进行等间隔采样，得到离散的数字中频信号：

r(n)=d(n)p(n)cosω0n+n(n)

(2)

1.2 重采样机理

由于本文研究的是基于非整数倍码元速率的采样率情况，因而需要做非整数倍的采样率变换。可以先作I倍内插再作D倍抽取来实现，即将采样率变为原来的I/D倍，需要注意的是必须内插在前、抽取在后，以确保中间序列的谱宽度满足信号无失真恢复的最小要求。非整数倍采样率变换的实现框图[9]如图2所示。

图中将2个级联的低通滤波器等效为1个低通滤波器，带宽为minπ/D,π/I，I表示I倍内插器，D表示D倍抽取器。

2 伪码估计方法

一段受到空中噪声污染的短码直扩信号的中频采样信号波形如图3所示。

本文方法直接对接收端中频采样的空中信号做处理，处理流程如图4所示。

首先估计出伪码采样信号周期和伪码起始点两个参数，在此基础上进行信号重采样，最后实现伪码估计。

2.1 相关参数估计

2.1.1伪码采样信号周期估计

(3)

式中，M为数据分段数，L为每段数据包含的采样点数；Sm(τ)为第m段数据的自相关值，P(τ)为分段自相关的模和。

对图3所示的中频采样信号进行采样数据分段，画出自相关叠加谱图如图5所示。

2.1.2伪码起始点估计

窗口1每滑动一个采样点，窗口2要滑动一个区间的采样点，计算内积值prt=〈w1,w2〉，则可得到一个内积值数组，以其中的最值作为窗口1的起点在当前采样点时的前后信号窗口内积值。逐个采样点地滑动窗口1，当前后信号窗口内积值单调变化并且正负发生改变时，改变之前的内积最值对应的窗口1起点即为rst1。

2.2 信号重采样实现

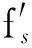
(4)

在2.1节中，已经找出采样信号r中的伪码起始点rst1，从该点取出之后的采样信号：

(5)

以式(4)确定的新的采样率对r(1)重采样：

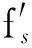
(6)

以上即完成了对接收端数字中频采样信号的重采样。

2.3 伪码估计

完成信号重采样之后，每段伪码周期上均有相等的采样点数，从伪码起始点提取出k段连续的伪码重采样信号，分析其调制样式，再以软件无线电的方法[9]实现解调得到伪码序列。下面以常见的2DPSK调制样式为例，说明伪码估计的具体方法。

r(3)=r1(2),r2(2),…,rk(2)

(7)

3 实验与结果分析

实验的相关参数设置如表1所示。

表1 实验参数设置Tab.1 Parameters forexperiment used

3.1 伪码估计实验

3.1.1伪码起始点估计实验

滑动信号窗口，画出前后窗口内积值如图7所示，寻找伪码起始点rst1；依次寻找各个伪码起始点，进而计算出各段伪码采样点数Ni如图8所示。

3.1.2信号重采样实验

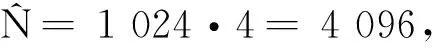
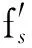
经过重采样后，信号在时域上的采样点更加密集，时域波形更加准确真实。

3.1.3伪码恢复实验

对重采样后的采样信号按2.3节的方法处理，遵循伪码0、1分布平衡的原则，等间隔选取合适的抽样判决点，输出最优伪码序列，结果如图10所示。

与实验设置的伪码序列比较，恢复出的伪码序列达到了100%的正确率。

3.2 对比实验

以经典的矩阵特征分解方法为对比，说明本文方法在非整数倍码元速率的采样率情况下的可靠性。矩阵特征分解方法恢复的伪码采样序列如图11所示。

4 结论

本文提出了基于重采样技术实现短码直扩信号伪码估计的方法。该方法直接对空中截获的中频采样信号进行处理，通过重采样使得每个直扩信号码元上的采样点数变为相等的整数个，即将非整数倍采样问题简化为整数倍采样问题，最后用数字正交解调实现伪码估计。实验结果表明，方法能够克服非整数倍码元速率的采样率情况下伪码估计时抽样判决点选取的不确定性，实现有效可靠的伪码估计。方法克服了采样设备的采样率限制，提高了伪码估计的鲁棒性，估计出的伪码序列可为之后进行欺骗干扰提供有效支持，具有较高的工程应用价值。

参考文献:

[1]赵鸿图，茅艳.通信原理MATLAB仿真教程[M].北京：人民邮电出版社，2010.

[2]张天琪，周正中.直扩信号的谱检测和神经网络估计[J].系统工程与电子技术，2001，23(12)：12-15.

[3]罗军辉，姬红兵，江莉.直接序列扩频信号PN序列盲估计方法[J].电子科技大学学报，2008，37(4)：480-492.

[4]秦怡，田斌.直扩信号伪码的盲估计方法的研究[J].现代电子技术，2007(3)：54-56.

[5]强幸子，张天琪，赵军桃，等.非合作直扩信号伪码及信息序列联合盲估计[J].重庆邮电大学学报(自然科学版)，2016，28(4)：468-472.

[6]张花国，李立萍，陈天麒.一种DS/SS信号盲同步算法[J].电子科技大学学报，2007，36(2)：207-209.

[7]张天琪，张传武，林孝康，等.直扩信号伪码周期及序列的估计算法[J].系统工程与电子技术，2005，27(8)：1365-1368.

[8]张天琪.直扩信号的盲处理[M].北京：国防工业出版社，2012.

[9]杨小牛，楼才义，徐建良.软件无线电原理与应用[M].北京：电子工业出版社，2001.

[10]罗名君，史英春，张旻.基于分层处理的短码直扩信号盲解扩算法[J].探测与控制学报，2017，39(1)：26-30.

[11]张雪梅.直扩信号检测与参数估计方法研究[D].西安：西安电子科技大学，2014.