基于二维流场的炮口制退器效率计算
王振嵘,高跃飞,刘国志,郭张霞,陶 哲
(1.中北大学 机电工程学院,山西 太原 030051;2.山西北方机械制造有限责任公司,山西 太原 030009)
0 引 言
炮口制退器是通过控制后效期火药气体从侧孔流过的流量和速度来达到减小后坐阻力的一种炮口装置[1].在炮口制退器设计过程中,制退效率是最重要的设计指标,准确计算炮口制退器效率对于缩短设计周期和节约经济成本具有重要意义.由于火药气体在炮口处的流动状态为高温高压高流速,流动情况复杂,而现有理论计算方法均为半经验半理论方法,其引入较多假设和经验系数,所以导致炮口制退器效率的计算误差较大.随着CFD(Computational Fluid Dynamics)技术的发展,通过求解炮口流场控制方程,得到身管后效期所受全冲量,进而根据动量守恒定理计算出炮口制退器效率的方法被广泛采用.但是由于炮口制退器不具有轴对称特点,将计算模型直接简化为二维模型计算会导致较大误差[2],而三维模型计算虽然准确度较高[3],却面临着网格数量巨大、对计算机配置要求高、计算时间长等问题,所以准确计算炮口制退器效率与计算时间短、对计算机资源要求低之间的矛盾成为了利用CFD技术计算炮口制退器效率的难点.本文从气体动力学角度出发,通过计算反作用式炮口制退器侧孔气流总反力来对二维炮口流场计算结果进行修正,以期利用网格数量小、计算时间短的二维计算模型来达到三维计算的准确度.为炮口制退器效率计算提供一种计算效率高的方法.
1 理论计算
1.1 基于CFD的效率计算方法
利用CFD技术求解炮口制退器效率[4]是通过计算发射过程中火炮后坐部分的全冲量来直接计算炮身最大自由后坐速度,进而求得炮口制退器效率.由于该方法避免了通过经验公式计算火药气体作用系数和炮口压力随时间的变化情况,因此具有较高的准确度.
根据炮口制退器效率的定义公式可得
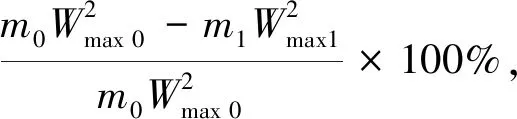
(1)
式中:E0,E1分别为不带和带炮口制退器时的最大后坐动能;Wmax 0;Wmax1分别为不带和带炮口制退器时后坐部分的最大自由后坐速度;m0为弹丸质量.
后效期过程中炮身做自由后坐运动,满足动量定理
miWmax i-miWi=Ii,
(2)
式中:下标i取值为0或1,分别代表不带和带炮口制退器时的情况;Wi为后效期开始时,自由后坐速度;Ii为后效期后坐部分受到的全冲量;Wmax i为后效期结束时最大自由后坐速度.
根据动量守恒定理,在后效期开始时刻有方程
miWi+ωvg+qv0=0,
(3)


(4)
式中:τ为后效期持续时间;Fi为不同时刻炮身的受力.
联立式(1)~式(4),即可得到炮口制退器效率ηT.
1.2 二维流场修正计算
由上述基于CFD的炮口制退器效率计算方法可知,求解制退器效率的关键在于后效期身管所受全冲量的计算.在Fluent中,三维炮口流场计算模型可以较为准确地计算后效期身管受力情况[5],通过对其进行积分运算,即可得到身管所受全冲量.而使用二维轴对称模型计算炮口流场时,炮口制退器纵向截面绕轴旋转形成环形侧孔结构(见图 1),与炮口制退器实际模型(见图 2)有较大差别.而侧孔面积增大,导致二维计算结果远大于三维计算结果.
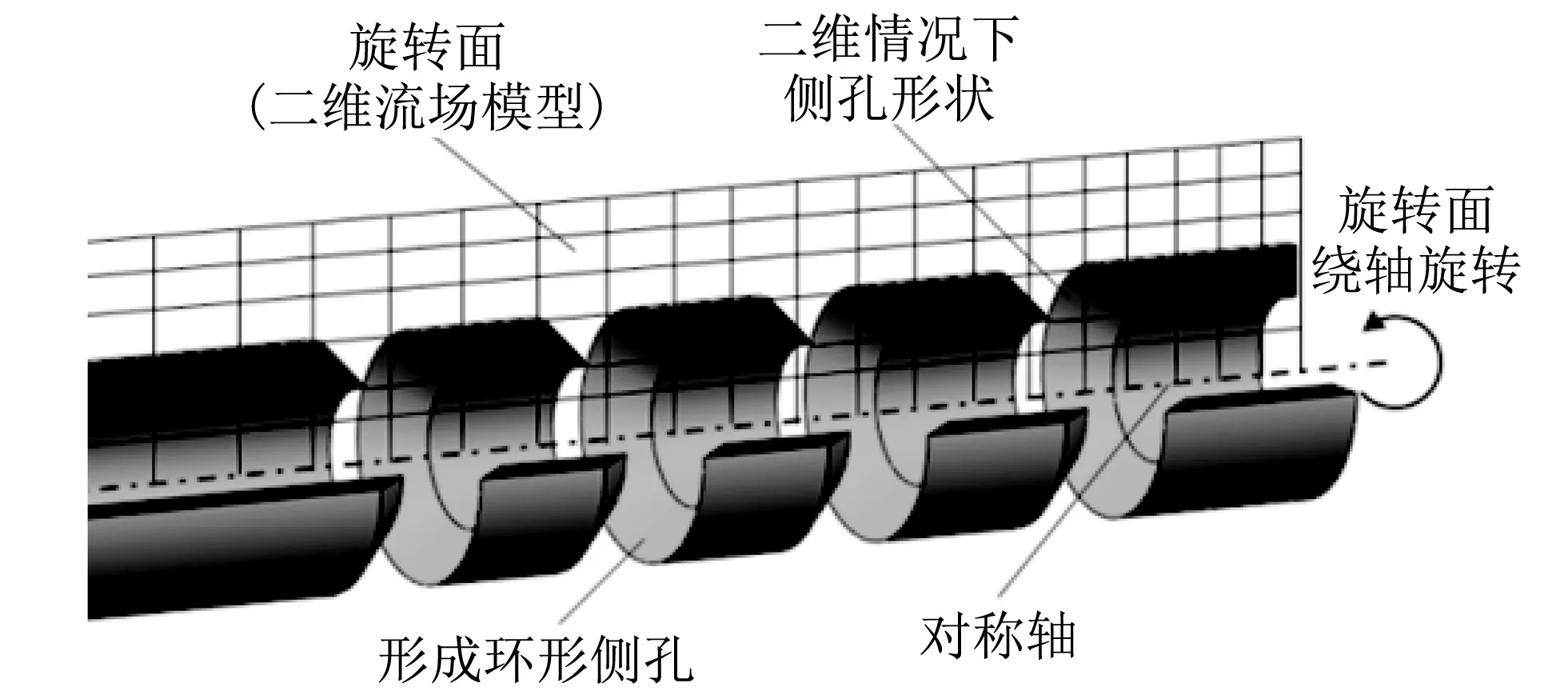
图 1二维轴对称模型三维等效示意图 Fig.1 3D equivalent diagram of 2D axisymmetric model
为修正二维计算结果,本文从气体动力学角度出发,分别计算炮口制退器环形侧孔和实际侧孔结构下产生的气流总反力,得到每排侧孔的受力修正系数ξ,通过对二维情况下每排侧孔的受力进行修正计算,可以得到与三维模型等效的身管受力曲线,进而求解炮口制退器效率.
反作用式炮口制退器制退力主要由侧孔气流总反力产生,根据气体动力学相关理论[6]可知,气体经过管道膨胀加速后淹没流出,产生的气流总反力为
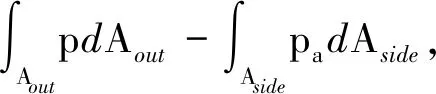
(5)
式中:ρ为气流密度;v为流体速度;p为单元面积中心压力;pa为大气压;A为控制体面积;Ain为入口面积;Aout为出口面积;Aside为大气压作用面积;V为控制体;S为控制面.
火药气体经过侧孔膨胀加速流出的过程可以看做一维准定常流动,故式(5)忽略加速度项和大气压力,可以得到侧孔气流总反力为
Fb=ρv2A+Ap,
(6)
式中:A为侧孔出口面积;v为侧孔出口截面平均速度;p为侧孔出口压力.
根据马蒙托夫所做出的假设[7]:炮口处为临界截面,对于反作用式炮口制退器即第一排侧孔处出现临界流动,故第一排侧孔入口处压力[8]为
p1=pk0,
(7)
式中:pk0为炮口压力.
第i排侧孔入口处压力为
pi=χi-1pk0,
(8)
式中:χi-1为轴向压力降系数,由式(9)求得
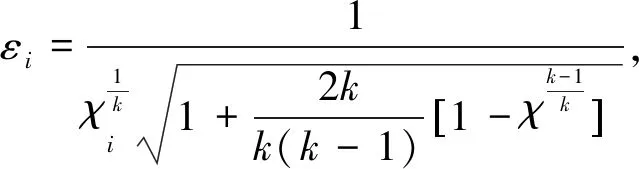
(9)
式中:k为绝热指数,对于火药气体产物一般取k=1.33;εi为流量出口面积比
(10)
式中:A0为炮膛横截面积;μci为气流截面收缩系数;Aci为第i排侧孔入口面积.
侧孔入口处气流速度vci和出口处气流速度vei为
(11)
式中:λi为侧孔膨胀系数;pi为侧孔入口压力;ρi为侧孔入口密度.
由于火药气体经过腔室和侧孔的速度很快,气体温度下降很小,故可以近似认为
(12)
联立式(7)~式(12)可以得到炮口制退器各侧孔火药气体产生的气流总反力的轴向分力
(13)
式中:χci为侧孔出口和入口压力降系数;α为侧孔倾角.
定义炮口制退器环形侧孔气流总反力和实际侧孔气流总反力的比值ξ为二维修正系数
(14)
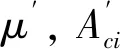
从式(14)可知,二维修正系数ξi的取值只由侧孔结构决定,而与时间无关.因此二维情况下侧孔受力Fbi(t)可由式(15)进行修正.
(15)

后效期自由后坐部分轴向受力主要包括身管受力和炮口制退器受力,而反作用式炮口制退器受力主要由侧孔气流总反力产生,因此带炮口制退器时,后效期自由后坐部分整体受力为
F=FB+FM,
(16)
式中:FB为身管受力;FM为炮口制退器受力.
(17)
得到后效期自由后坐部分整体受力F后,代入式(1)~式(4)即可求得炮口制退器效率.
2 炮口制退器模型
本文以反作用式炮口制退器为例进行效率的计算.反作用式炮口制退器的特点是腔室直径小,没有或只有很小的反射挡板,火药气体通过多排侧孔膨胀加速后高速喷出,一方面通过侧孔产生的气流总反力来提供与炮膛合力相反的制退力,另一方面由于部分火药气体从侧孔流出,使得中央弹孔的火药气体流量减小,降低了后坐动能.本文以某加装反作用式炮口制退器的23 mm小口径火炮为例进行效率计算,其三维模型如图 2 所示,炮口处对称设计5排面积相同的条形侧孔结构,侧孔后倾角为135°,腔室直径为24 mm.
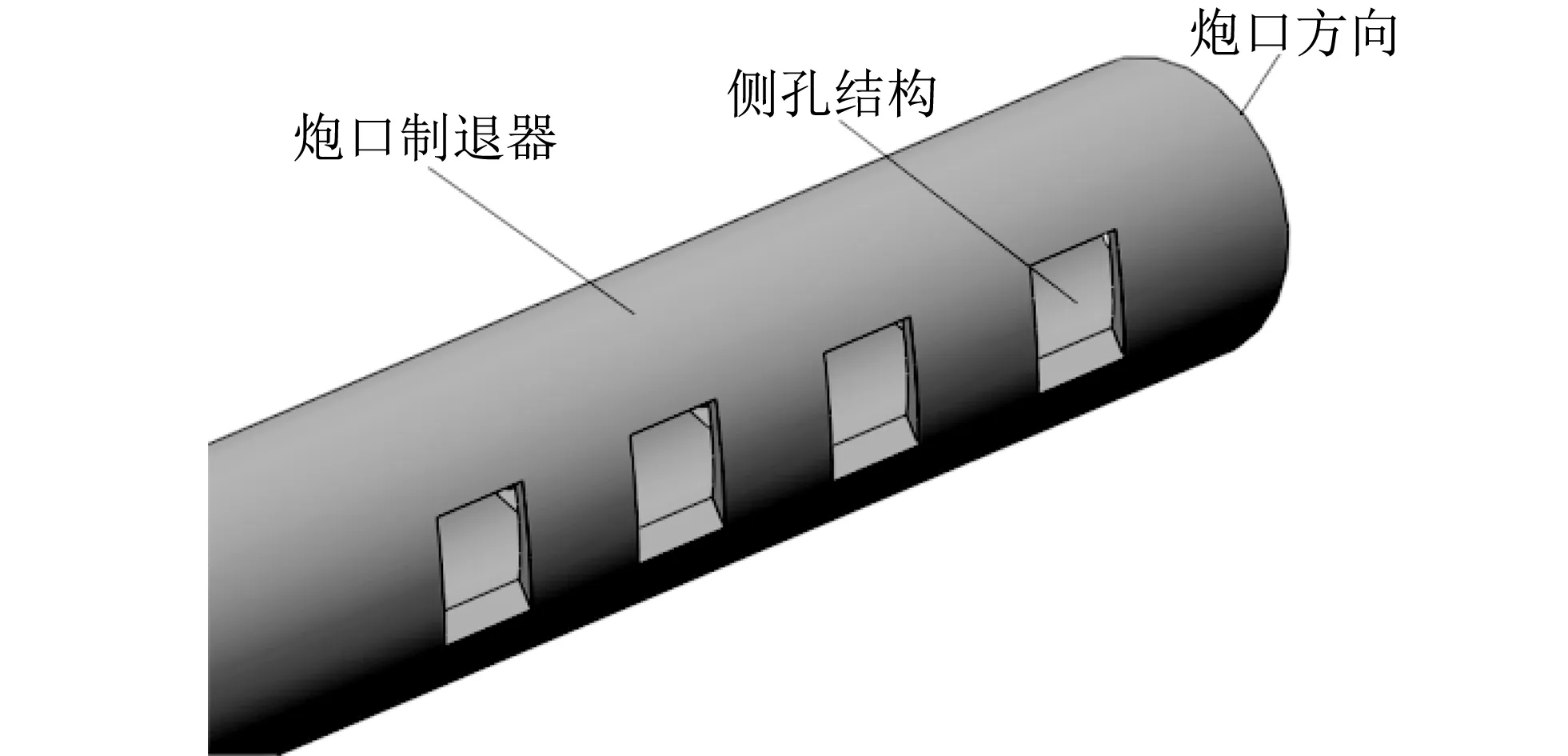
图 2炮口制图器三维结构图Fig.2 3D structure diagram of muzzle brake
3 仿真与分析
3.1 计算模型与边界条件
火炮发射过程中,膛内火药气体为气固两相流,并且包含了多组分运输、燃烧等物理化学变化,建立真实的仿真模型较为困难,因此在工程中一般都基于以下假设,对其进行合理简化[9]:
1) 将空气和火药气体当作同一介质,采用理想气体的材料特性来计算;
2) 不考虑弹丸,忽略弹丸运动对气体的影响.
基于以上两点假设,本文采用Euler方程来描述炮口流场[10];湍流模型选择适合壁面问题求解和捕捉激波的Spalart-Allmaras模型;边界条件采用压力出口条件和滑移壁面条件.在控制方程及边界条件确定后,通过Fluent软件进行求解.
3.2 三维计算模型验证
目前,通过对三维模型进行仿真分析来计算炮口制退器效率的方法已经被广泛采用.张辉[4]曾针对三维炮口制退器模型,通过动量守恒定理和流体仿真手段计算了炮口制退器效率.本文采用同样的仿真模型计算三维情况下炮口制退器效率,为验证模型的正确性,对某100 J火炮进行仿真计算,计算模型如图 3 所示.

图 3炮口制退器网格模型Fig.3 Mesh model of muzzle brake
通过对某100 J火炮的仿真计算(计算结果如图 4),根据式(1)~(4)可得到炮口制退器效率为42.7%,而该火炮实测效率为45%,仿真结果与实测数据较为接近,验证了仿真模型的正确性.

图 41 ms时刻炮口压力云图Fig.4 1 ms muzzle pressure contour map
3.3 二维修正计算结果
针对本文研究对象——某23 mm小口径火炮,采用同样的仿真模型进行计算,膛内区域根据其内弹道特性进行初始化,该23 mm火炮的速度、压力、温度沿身管轴向分布情况如图 5 所示.

图 5膛内区域各物理量分布规律Fig.5 Distribution law of physical quantity in bore
分别对二维情况和三维情况下身管受力情况进行仿真,并计算炮口制退器效率,计算模型如图 6 所示.
以二维计算结果为例分析炮口流场.如图 7 所示,选取4个时刻的炮口流场压力等值线图进行分析.火药气体从炮口喷出的过程为非定常流动,产生的瓶状激波会经历生长、稳定、衰减的过程,从仿真结果可以看出,0.25 ms时流场处于生长阶段,1 ms和2 ms处于稳定阶段,而5 ms瓶状激波逐渐衰减,与实际流动状态相吻合.
在二维仿真过程中,监测身管和各侧孔的受力情况,可以得到受力随时间变化曲线Fbi(t), 如图 8 所示,根据式(15)进行修正并计算后效期整体受力曲线F,即可得到二维修正计算结果,通过与三维情况下自由后坐部分整体受力曲线对比(见图 9),可以看出两种计算结果曲线基本重合,验证了本文提出的计算方法的正确性.
分别对三维情况下受力曲线和二维修正后的受力曲线进行积分计算,可以得到后效期身管所受全冲量为44.56 N·m,47.21 N·m,根据式(1)~式(4)计算炮口制退器效率分别为26.89%,24.75%,二维和三维计算结果较为吻合.
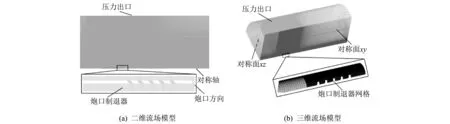
图 6炮口制退器流场计算模型 Fig.6 Muzzle brake flow field calculation model

图 7不同时刻炮口流场压力等值线图Fig.7 Muzzle pressure contour map at different times
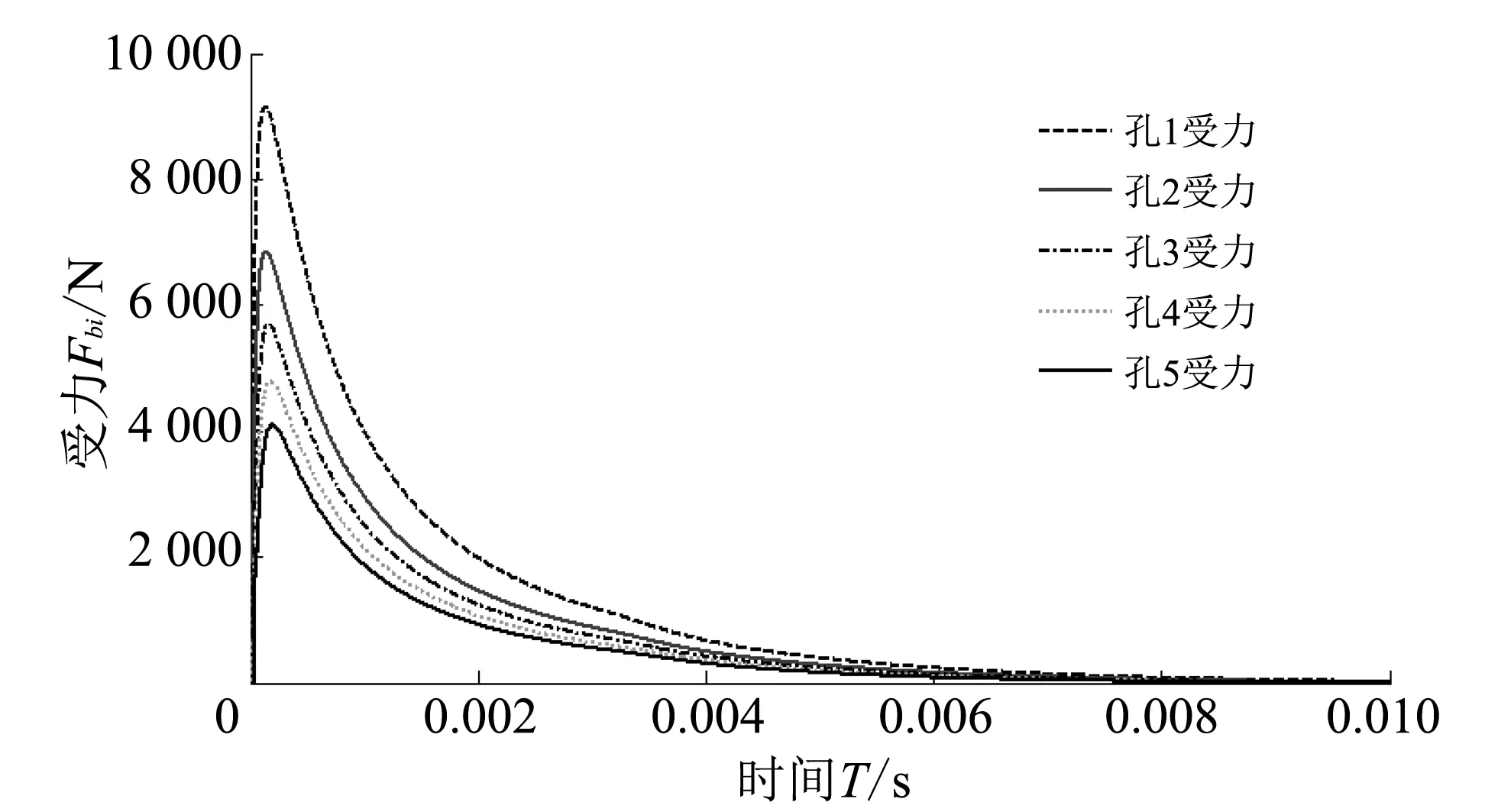
图 8二维情况下各侧孔受力Fig.8 Side hole force in 2D
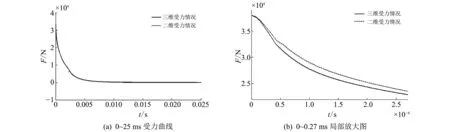
图 9二维修正结果与三维计算结果对比Fig.9 Comparison of 2D correction results and 3D calculation results
4 结 论
针对三维流场计算炮口制退器效率时间长、需要计算机资源大等问题,提出了利用气体动力学相关理论修正二维流场来计算炮口制退器效率,以某反作用式炮口制退器为例进行仿真分析,通过对比三维和修正后二维计算结果可知,本文提出的二维修正方法可以等效三维计算模型,并具有足够的准确度,可为炮口制退器设计及优化提供便利.

