基于双线性软化模型鲁灰花岗岩断裂特征研究
林建伟,高经武,武晋文,王学怀,吕 琪
(中北大学 理学院,山西 太原 030051)
0 引 言
大量研究表明,岩石的破损可以认为是微裂隙的发展过程[1].随着裂缝扩展,岩石刚度下降,粘聚力削弱,这种现象称为岩石的软化[2].在软化现象中,岩石和其他脆性材料的断裂表现为裂纹尖端附近的一个非线性区域,称为断裂过程区.岩石的软化现象与其断裂过程区移动息息相关,过程区的确定对分析脆性材料断裂的力学性能至关重要[3].确定断裂过程区的方法包括直接法和间接法.直接法基本思想是通过声波发射法[4]和数字散斑测量法等[5],直接对断裂过程区的材料断裂和开口位移进行测量.间接法则是通过对实验结果的参数拟合来间接识别过程区[6].
20世纪70年代后期,Hillerborg[7]提出脆性材料虚拟裂缝模型(也称粘聚裂缝模型),虚拟裂缝模型把裂缝分解为真实物理裂缝(完全开裂区)和虚拟裂缝(微裂缝区)两部分.该模型在断裂力学中得到了广泛的应用.Hillerborg通过将混凝土直接拉伸实验的应力-应变软化曲线近似为一条直线,提出直线型软化曲线,对其断裂过程进行分析,从中给出特征长度的概念,认为特征长度与断裂过程区长度存在着一定的关系.
单线性软化关系不能准确地反应粘聚应力与裂缝张开位移的关系,对断裂过程的分析有较大的影响.基于Hillerborg的工作,很多学者在随后的研究中进一步提出了双线性软化曲线.双线性曲线的关键在于转折点的选取,根据不同材料实验结果分析,对于转折点的取值给出了多种经验性的公式.其中,Petersson[8]假定转折点粘聚应力与抗拉强度比值为1/3,从而得到软化曲线.对此,M.Elices[9]提出了另一种混凝土软化曲线的双线性曲线,采用抗拉强度、断裂能、软化曲线面积形心横坐标和初始线性部分延伸线的水平截距四个参数建立混凝土软化曲线,避免了对材料经验性参数的确定,并提出断裂与混凝土骨料的大小相关.徐世烺[10]基于上述理论针对混凝土骨料大小与软化曲线的关系给出了混凝土双线性修正公式.
脆性材料软化曲线描述了断裂过程区的特性,是很多脆性材料断裂模型的基础,尤其是在有限元程序模拟脆性材料非线性性能的时候,软化曲线与抗拉强度以及断裂能是必要的输入参数.因此,建立岩石软化模型对岩石断裂分析有着重要意义.目前,对岩石断裂的分析,多数通过直接观察,或通过分析摩擦角和粘聚力的变化来描述岩石软化和断裂过程,而通过建立脆性材料软化模型来分析岩石断裂过程的研究较少.基于脆性材料软化的双线性模型,本文建立鲁灰花岗岩软化模型,对其断裂特性进行分析,得到其临界裂缝尖端张开位移wq和临界裂缝张开位移wc.
1 脆性材料双线性软化曲线
M.Elices等[9]提出的双线性模型对于微裂区(如图 1)做出以下假设:
1) 对于软化曲线,当预制裂缝尖端最大主应力σ1达到粘聚力强度临界值(抗拉强度)σt时,粘聚裂纹开始出现,此时应力值为软化曲线的起始值,粘聚裂纹与主应力的方向垂直.
2) 微裂缝出现,微裂缝面之间的粘聚应力是裂纹张开位移的函数.对于I型裂纹,粘聚应力σ与裂纹面垂直,是裂纹张开位移w的一元函数
σ=f(w),
(1)
式中:f(w)称为软化函数.抗拉强度σt是微裂缝萌生的初始应力,即
σt=f(0).
(2)
断裂能Gf是裂缝完全张开(粘聚应力σ=0)单位面积所消耗的能量,由软化曲线下的面积给出,如图 1(b) 所示,即

(3)
式中:wc为临界裂缝张开位移,裂缝超过wc后粘聚应力变为零.

图 1断裂过程区模型和软化曲线Fig.1 The cohesive zone model and softening curve

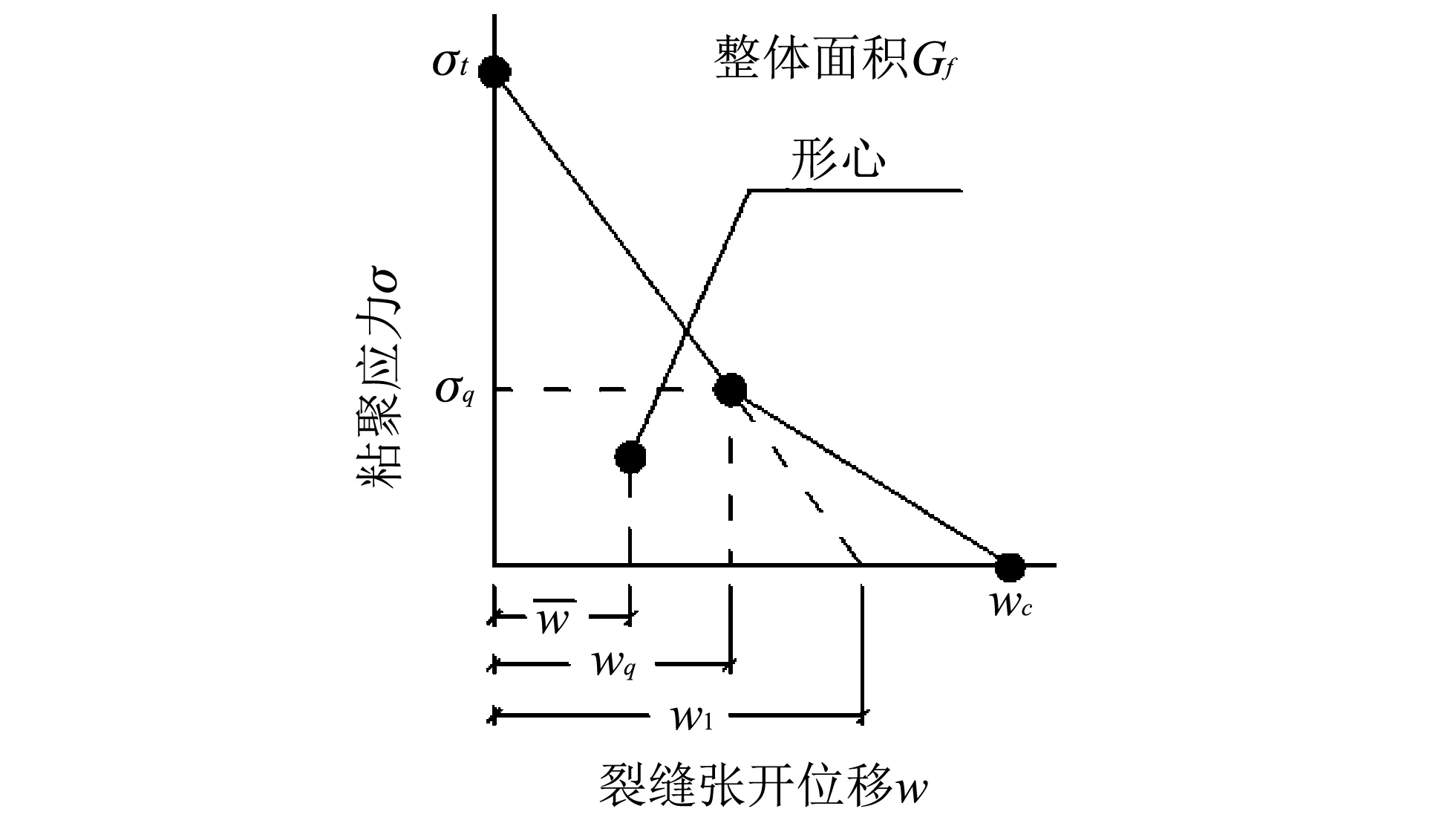
图 2双线性软化曲线Fig.2 Bilinear softening curve
2 鲁灰花岗岩双线性软化曲线
2.1 双线性曲线参数的确定
2.1.1 抗拉强度σt
采用巴西劈裂实验测定鲁灰花岗岩抗拉强度:
(4)
式中:σt为抗拉强度;Pu为最大载荷;t为圆柱体长度;D为圆柱体的直径.
巴西劈裂试样为Φ50 mm×25 mm的圆盘,通过公式得到鲁灰花岗岩的抗拉强度在9.35~11.4 MPa之间,平均值为10.355 MPa,具体测试结果见表 1.

表 1巴西劈裂实验测试结果

图 3试样制备及规格Fig.3 Specimen preparation and specification
根据Rilem[11]提出的计算方案,断裂能Gf表达式为
(5)
式中:WF为带预制裂缝的矩形梁试件静态断裂所做的功;B,H分别为试件的厚度和高度;a0为预制裂缝的长度.

(6)
式中:α为一个无量纲参数,取决于软化函数的形状,对于双线性型软化曲线,应取α=0.987[8].
Manuel Elices等[13]认为双线性软化曲线转折发生在三点弯曲的峰值荷载后,w1与断裂能和抗拉强度的比值相关,根据Guinea G V等[14-15]给出w1的确定方法,得到鲁灰花岗岩w1计算公式为
(7)


图 4三点弯曲实验荷载-挠度曲线Fig.4 Load-deflection curve at three point bending test

试件编号跨径l/mm厚度B/mm高度H/mm预制裂缝长度a0/mmW-116021.1638.0017.56W-216020.6538.8217.05W-316019.2938.4517.20平均值16020.3738.4217.27试件编号抗拉强度σt/MPa断裂能Gf/(N·mm)曲线面积形心横坐标/mm曲线前段水平截距w1/mmW-110.3550.2290.021 80.017 7W-210.3550.1700.016 20.013 2W-310.3550.2060.019 70.015 9平均值10.3550.2020.019 20.015 6
2.2 双线性型软化曲线的确定


(8)
双线性软化曲线拐点对应的坐标wq和σq表示为
(9)

(10)

图 5鲁灰花岗岩软化曲线Fig.5 The softening curve of Lu grey granite
由图 5 表示的软化曲线,可将鲁灰花岗岩断裂过程分为起裂、稳定扩展和失稳扩展三个阶段[10].起裂阶段,即w=0时,初始裂缝尖端处的粘聚应力等于其抗拉强度σt;裂缝张开位移从零到wq为稳定扩展阶段,裂缝张开位移为wq时,裂缝处于稳定扩展的临界状态,岩石的粘聚应力下降到抗拉强度的50%,岩石刚度减小,粘聚力减弱;裂缝张开位移从wq到wc为失稳扩展阶段,当裂缝张开位移达到临界裂缝张开位移wc时,粘聚应力为零,形成宏观裂缝.
根据鲁灰花岗岩软化曲线,拐点处裂缝张开位移wq在0.007~0.009 mm之间,临界裂缝张开位移wc在0.05~0.07 mm之间.鲁灰花岗岩双线性软化曲线模型参数分别为:σt=10.355±0.876 mm;wq=0.008 0±0.000 8 mm;wc=0.062 3±0.005 5 mm.花岗岩是非均质材料,模型参数有一定的离散性,相对平均值离散程度为9%左右.
3 实验验证与分析
Shah S P[16]采用声波观测的方法证实预制裂缝尖端的张开位移的临界值(CTODc)为材料属性,与试件尺寸无关,可作为判断材料失稳断裂的材料参数,并且根据实验数据发现转折点wq与实验测得的CTODc比较接近.基于上述研究,徐世烺[10]采用改进的双线性公式,认为在三点弯曲实验中,荷载达到峰值时,CTODc对应双线性软化曲线上转折点的横坐标wq,此时粘聚应力对应转折点处的σq.
鉴于上述研究结果,将测定的鲁灰花岗岩峰值荷载下预制裂缝尖端张开位移CTODc与wq进行对比,以此验证双线性软化曲线的合理性.
3.1 实验设备
实验设备包括电子万能试验机和ARAMIS三维全场动态应变测试系统,如图 6 所示.设置加载速率为0.05 mm/min,图像采集频率为2 Hz/s,DIC分辨率为2 448×2 050,物面分辨率为0.021 95 mm/像素,位移精度为0.01像素,实际位移精度为0.000 219 5 mm.

图 6DIC测试设备Fig.6 DIC test equipment
如图 6,在试样预制裂缝尖端同一水平上取点1和点3,两点之间的距离变化即为预制裂缝尖端的CTOD,峰值荷载时对应CTODc.
3.2 实验结果与分析
图 7 为鲁灰花岗岩三点弯曲实验中DIC数字散斑测量系统测得的加载过程中荷载P与裂缝尖端张开位移CTOD的关系.70%~80%峰值荷载前P-CTOD曲线呈线性关系,70%~80%峰值荷载到峰值荷载,P-CTOD曲线呈非线性,此阶段材料内部存在较好的粘聚力,对应软化曲线的裂缝稳定扩展阶段;当荷载超过峰值,粘聚应力大幅降低,进入失稳破坏阶段.表 3 为本文建立的鲁灰花岗岩双线性软化曲中关键点(wq与wc)数值与实测数值的对照表.实验测定的峰值荷载时刻预制裂缝尖端裂缝张开位移CTODc在0.008~0.011 mm之间,平均值0.009 mm;软化曲线计算得的临界裂缝尖端张开位移wq为0.007~0.009 mm,平均值为0.008 mm,两者接近.这与徐世烺提到临界裂缝尖端张开位移与峰值荷载下CTOD接近的结论一致,验证了所建鲁灰花岗岩双线性软化曲线的合理性.

图 7 三点弯曲实验P-CTOD曲线图Fig.7 P-CTOD curve at three point bending test

编号模型峰值荷载下裂缝尖端张开位移wq/mm实测峰值荷载下裂缝张尖端开位移CTODc/mm模型临界裂缝张开位移wc/mm实测最大裂缝尖端张开位移CTODm/mmW-10.0090.0080.0700.117W-20.0070.0080.0530.117W-30.0080.0110.0640.127平均值0.0080.0090.0620.120
由表 3 可知,双线性软化曲线中,临界裂缝张开位移wc为0.053~0.07 mm,根据虚拟裂缝模型假设,wc为岩石失去粘聚应力的临界状态.虽然wc对于材料本身来讲是一个很重要的断裂参数,但在实验过程中没有明显的断裂特征与其对应,故无法通过实验直接测量其准确数值.验证实验结束时测得最大裂缝张开位移CTODm为0.117~0.127 mm,由软化模型计算得到的wc介于CTODm和CTODc之间,大约是CTODc的 7~8 倍.
4 结 论

临界裂缝尖端张开位移CTODc作为材料断裂属性,裂缝张开位移CTOD达到这一数值时,岩石失稳破坏开始.根据鲁灰花岗岩双线性软化曲线,其临界裂缝尖端张开位移wq为0.007~0.009 mm.通过实验方法测定临界裂缝尖端张开位移平均值为0.009 mm,验证了鲁灰花岗岩双线性软化曲线的合理性.
鲁灰花岗岩软化曲线中临界裂缝张开位移wc为0.05~0.07 mm,大约是wq的7~8倍.wc为岩石内部粘聚力为零的裂缝张开位移,是微裂缝区的末端.

