直升机吊挂飞行旋翼桨毂载荷分析

孙国普，曹普孙，陈笑天，张义涛

(1.中国直升机设计研究所，江西 景德镇 333001；2.陆军装备部驻景德镇地区航空军事代表室，江西 景德镇 333001)

0 引言

吊挂飞行是直升机特有的一种飞行方式。这种方式能够不受地面地形和直升机自身货舱大小的限制，扩大了直升机的使用范围，使其在军用和民用领域具有不可替代的作用[1]。现今直升机吊挂飞行的应用日益增多，这背后离不开直升机科研工作者长期的技术支持。

针对直升机吊挂飞行的研究由来已久且备受关注。一直以来，关于建立准确、适当的直升机吊挂系统飞行动力学模型，并利用模型对直升机稳定性[2-5]、直升机飞行品质[6]、吊挂物抛放过程[7]等问题的研究不断，其颇丰的研究成果也多见于各类文献资料，但针对直升机吊挂水平前飞状态，吊挂挂点位置对直升机旋翼桨毂载荷影响的研究却较少。

鉴于此，本文假设吊挂为质点，建立直升机吊挂飞行动力学模型，并利用此模型，围绕挂点位置对旋翼桨毂载荷的影响开展分析研究，获得了一些有意义的结论，为吊挂飞行时减小旋翼桨毂载荷，提高桨毂使用寿命提供有力的技术支撑。

1 直升机吊挂飞行动力学模型的建立和验证

基于已有的直升机飞行动力学模型，添加吊挂系统模块，吊挂系统对直升机的影响等效处理成额外作用力及力矩，组建直升机吊挂飞行动力学模型。

1.1 吊挂模型

常见的吊挂系统中通常包括吊挂物和吊索，吊挂物和吊索的模型是吊挂建模的关键。本文假定吊挂物为一质点，仅受其自身重力、气动力和来自吊索的拉力作用，其中气动力模型来自文献[8]，仅为当地气流方向的准静态阻力；吊索视为弹性吊索，只能在伸长方向变化，无质量且不受气动力，且始终处于紧绷状态。

吊挂的几何模型如图1所示。吊挂坐标系的is,js,ks三轴分别平行于体轴系中的iB,jB,kB，其坐标原点位于挂点处，其中θs为吊索与ks轴的夹角，φs为方位角。因此，在吊挂坐标系中，吊挂物的坐标为：

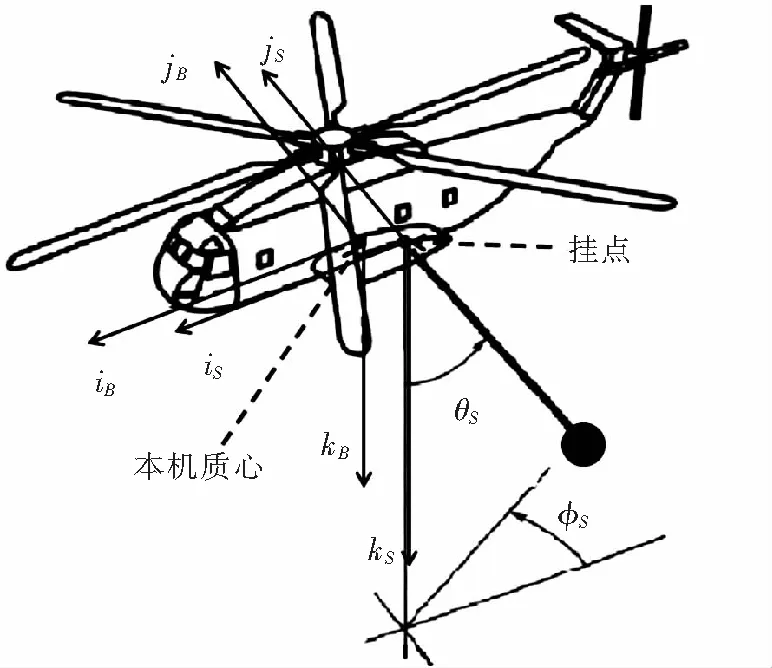
图1 吊挂飞行示意图[5]

Rs=-lsinθscosφsis+lsinθssinφsjs+lcosθsks

(1)

其中，l为吊索长度，而挂点在体轴系下的坐标为：

RB=xBiB+yBjB+zBkB

(2)

因此，吊挂物在体轴系中的坐标为RL=RB+RS，吊挂物的绝对速度和加速度在体轴系下分别为：

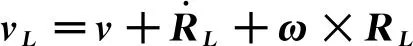
(3)

(4)

其中，v、a分别为机身质心的绝对速度和加速度，ω为机身的转动角速度向量。故而在体轴系下，吊挂物所受气动阻力为：

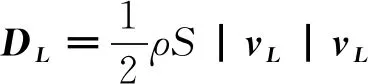
(5)

其中，ρ为空气密度，S为吊挂物的等效迎风面积。

吊索所受力为：

FL=-mLaL+DL+mLg=k·RL

(6)

吊索作用在机体的合力矩为：

ML=RB×FL

(7)

其中，mL为吊挂物的质量，g为重力加速度在体轴系中的向量，k为吊索的弹性系数。

1.2 直升机吊挂飞行动力学模型

直升机模型数据来自单旋翼带尾桨的常规直升机AC313直升机。模型中产生气动力的部件为旋翼、尾桨和机身，其中机身包含平垂尾；计算气动力时直接运用风洞数据；两旋翼的气动力计算方法基于经典叶素理论[9]；桨叶结构采用刚性桨叶。

直升机吊挂系统在机身质点的平动和绕机身质点的转动方程分别为：

(8)

M+ML=I·ω+ω×(Iω)

(9)

其中，mB为本机(无吊挂直升机)质量，g为重力加速度在体轴系内的向量，F与M分别为各部件气动力的合力和合力矩，v=(vx,vy,vz)T，ω=(ωx,ωy,ωz)T，I为机身的惯性张量。此外，g中所含的姿态角满足以下方程：

(10)

其中，θ=ϑ，γ，φ)T，C如下所示：

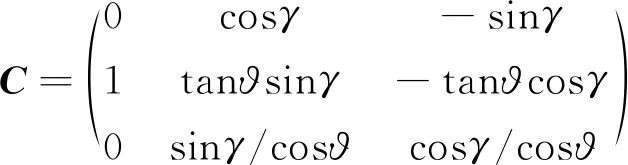
(11)

1.3 直升机吊挂飞行动力学模型的验证

图2同时给出了直升机带吊挂水平前飞时，计算和试飞所得操纵及机身姿态值，其中计算所用的总体参数值见表1。计算所得操纵及机身姿态随速度变化的趋势与试飞一致，仅在数值上与其略有差异，较好地吻合了试飞。

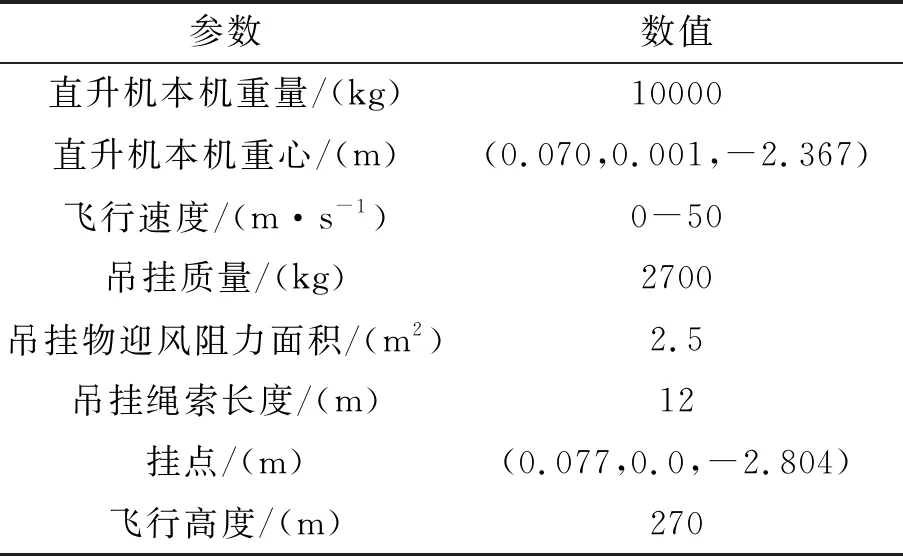
表1 总体参数

图2 飞行操纵和姿态

通过将计算所得操纵及机身姿态值与试飞数据相对比，验证了所建模型能得到较为精确的周期操纵及机身姿态值。周期操纵和机身姿态与桨盘倾角紧密相关，而旋翼桨毂载荷又与桨盘倾角成正比，因此，所建模型可用于吊挂飞行旋翼桨毂载荷的分析。

注：坐标值取值于以桨毂中心为原点的坐标系，该坐标系的详细定义见下文。

2 直升机吊挂飞行旋翼桨毂载荷的结果与分析

2.1 影响旋翼桨毂载荷的因素

旋翼桨毂载荷的大小与旋翼桨叶的片数、桨叶对挥舞铰的质量静矩、旋翼旋转角速度等物理量有关，其数学关系如下：

(12)

其中，MG为桨毂载荷(桨毂弯矩)，k为桨叶片数，MS为桨叶对挥舞铰的质量静矩，Ω为旋翼旋转角速度，e为挥舞铰外伸量，a1s、b1s分别为旋翼桨盘纵横倾角，其计算如下：

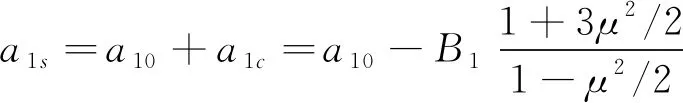
(13)

b1s=b10+b1c=b10+A1

(14)

其中:a10、b10分别为桨盘因吹风挥舞而形成的后倒角和侧倾角，其大小受总距、桨叶的扭转率，诱导速度等物理量影响;a1c、b1c分别为横纵向操纵挥舞;A1、B1为横纵向操纵量;μ为前进比。

从公式(12)可以知悉，旋翼桨毂载荷与旋翼桨盘合倾角成正比，而合倾角的大小与吹风挥舞和操纵挥舞的大小有直接关系。因此，对于在用直升机，桨毂载荷的大小由操纵挥舞和吹风挥舞共同决定。

与无吊挂飞行相比，有吊挂飞行会有额外的阻力和低头力矩，会迫使机身低头加剧，增大桨盘与水平面的夹角，使得旋翼产生的水平拉力增大，用以平衡吊挂带来的额外阻力。而当机身低头过大或不足，使得夹角增量不当时，还可以通过周期操纵来调节该夹角，以使得旋翼产生适当的水平分力。因此，与无吊挂相比，吊挂飞行会一定程度上改变飞行姿态和周期操纵，周期操纵的变化则会影响桨毂载荷。此外，吊挂飞行时，因挂点位置不同，其飞行姿态和操纵也会随着改变，最后导致桨毂载荷会有所不同。

2.2 挂点位置对旋翼桨毂载荷的影响

单点吊挂时，挂点位置依据直升机重心包线，可在直升机纵、垂向的某个区域内选取。表2给出了本文所选取用以研究的挂点位置。其中，坐标值所在的坐标原点位于桨毂中心，X轴正方向与直升机航向相反，Y轴沿航向右侧为正，Z轴垂直于X、Y轴向上为正。

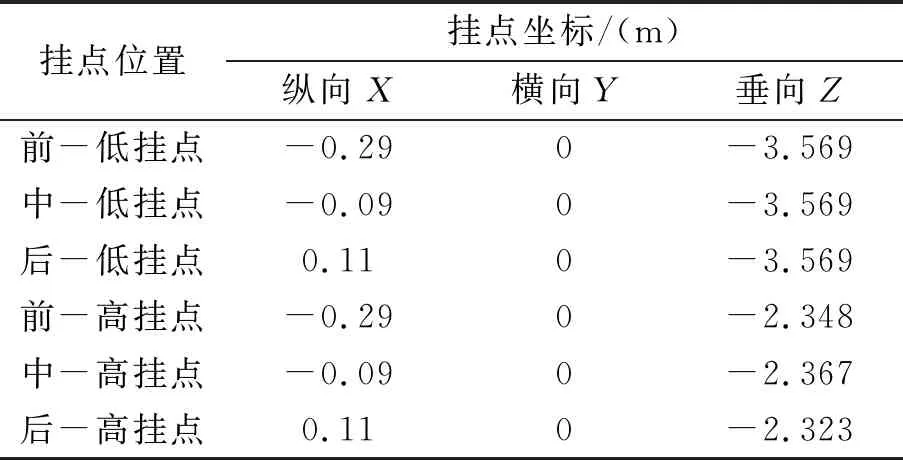
表2 挂点位置

前、中、后挂点坐标只在纵向(X轴)不同：前挂点与驾驶舱纵向距离最近，位于桨毂中心之前的0.29 m处，后挂点位于桨毂中心之后的0.11 m处，而中挂点位于前、后挂点之间。高、低挂点坐标只在垂向(Z轴)不同：相比于高挂点，低挂点与桨毂重心垂向距离较远，且位于11 t本机重心位置之下，而高挂点与11 t本机重心位置垂向坐标相同。11 t本机的不同重心位置坐标见表3。

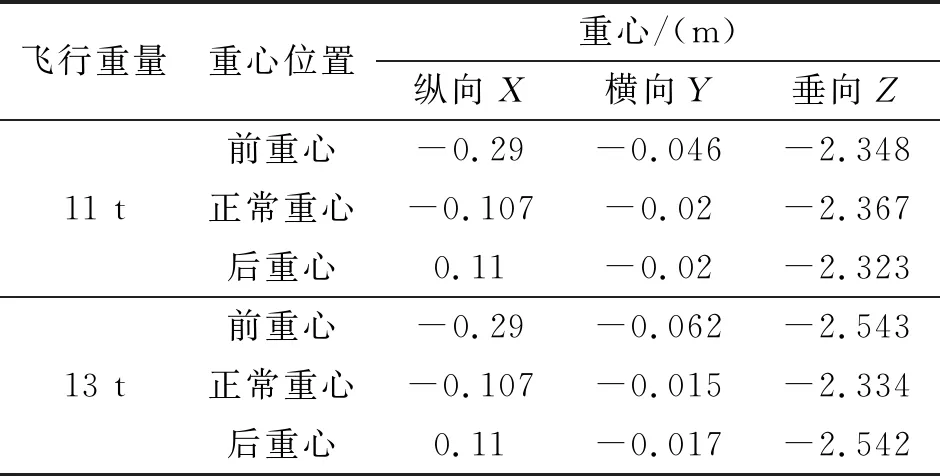
表3 不同质量本机的重心位置

本文先探索挂点位于本机重心时的桨毂载荷，其后依次研究挂点位置纵、垂向变化时对桨毂载荷的影响。为突显吊挂系统迎风阻力对直升机的影响，下文计算所采用的吊挂物等效迎风阻力面积设为5 m2。

2.2.1 挂点位于本机重心时对桨毂载荷的影响

图3给出了13 t本机处于不同重心位置时的桨毂载荷，以及本机与吊挂共13 t(11 t本机，吊挂2 t)，在不同本机重心位置且挂点位于相应本机重心时的桨毂载荷。可以看出，当总质量相同时，若挂点位于本机重心，吊挂几乎不会给桨毂带来额外的载荷，甚至在飞行速度大于40 m/s时，吊挂飞行的桨毂载荷还会变小。当飞行速度在40 m/s以内，相比于无吊挂，吊挂所带来的外阻力几乎不影响总距，致使旋翼的吹风挥舞几乎不受影响。对于操纵挥舞，从图4中可以知悉，纵向操纵几乎一样，横向操纵也是如此，故而桨盘合倾角几乎一致，桨毂载荷基本一致。而当飞行速度大于40 m/s时，吊挂阻力会影响总距，吊挂飞行较无吊挂时总距明显增大，吹风挥舞增强，使得桨盘合倾角减小，桨毂载荷变小。

从图5可知，当挂点位于本机重心时的吊挂飞行，与同质量的本机飞行相比，其低头姿态明显加剧，迫使旋翼水平拉力增大，以用于平衡吊挂阻力。结合上述分析不难知晓，当周期操纵和吹风挥舞在有、无吊挂基本相同时，桨盘与水平面夹角的增量几乎全部来自机身俯仰。

此外，从图3中还可以获悉，本机重心在纵向上越居于前，桨毂载荷越大。表4展示了飞行速度为50 m/s时，不同重心位置时本机旋翼的相关物理量。当本机重心在纵向移动时，旋翼的吹风挥舞变化微小，而周期操纵却相差很大。前重心时，机身低头2.77°，为最大。低头加剧，使得在吹风挥舞基础上还需向后带杆，机身才可维持平衡，后重心时却需向前带杆，故而桨盘横纵倾角相差很大，最终导致桨毂载荷相差很大。

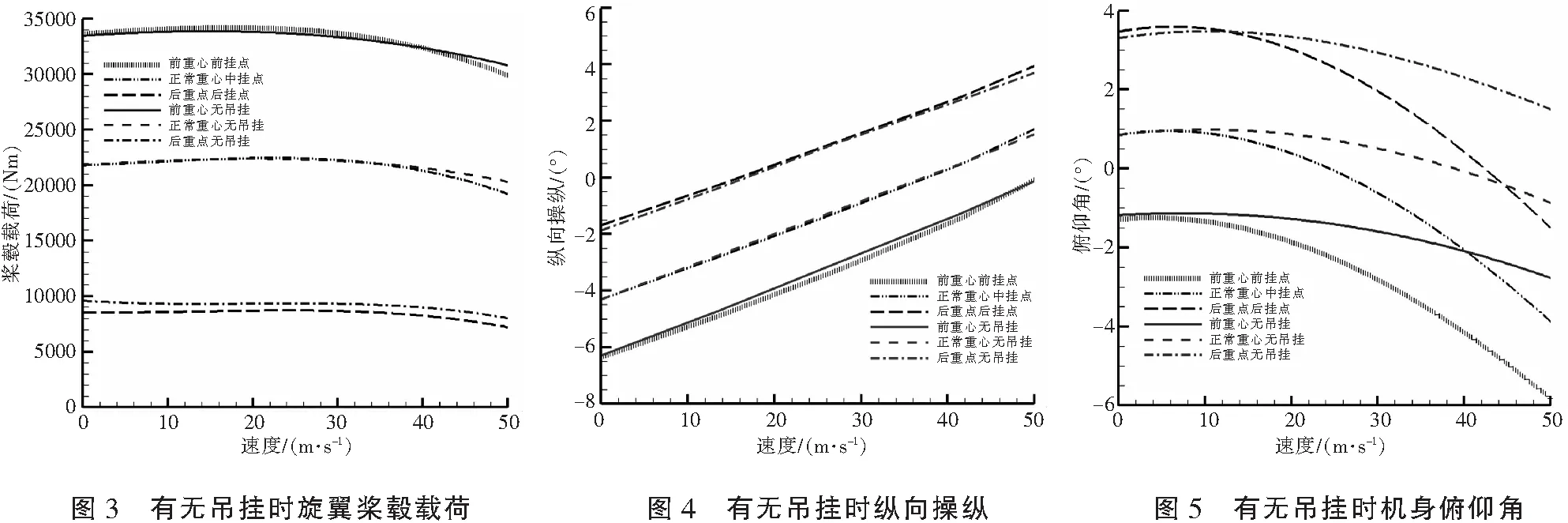
表4 本机13 t时不同重心位置的物理量(速度50 m/s)

2.2.2 挂点纵向变化对桨毂载荷的影响

当挂点位置只有纵向变化时，对桨毂载荷的影响见图6。此处的前、中、后挂点的坐标数值见表2后三行。不论本机重心处于哪个位置，前挂点的桨毂载荷都最大，后挂点的载荷最小。出现如此现象，与本机自身特点有关：由2.2.1中的分析可知，本机重心越靠前，桨毂载荷越大，类比于本机重心位置对桨毂载荷的影响，挂点处于前，相当于本机和吊挂整个系统的纵向重心，较挂点处于后时靠前，机身低头加剧，周期操纵使得桨盘横纵倾角增大，最终导致桨毂载荷增大。

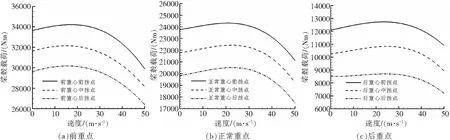
图6 不同重心不同挂点旋翼桨毂载荷

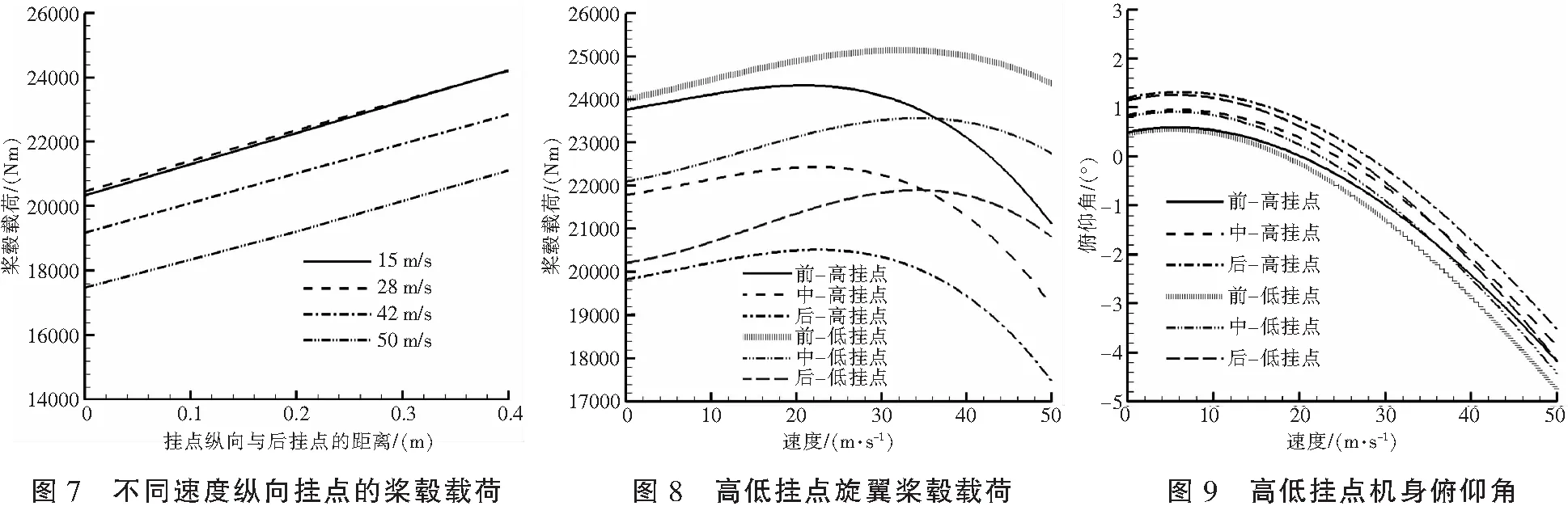
为进一步探究挂点纵向位置变化对桨毂载荷的影响，在处于正常重心的本机上，选取若干仅纵向位置不同的挂点，挂点的纵向处于距离后挂点0.4 m的区间内。图7给出了不同飞行速度下，不同纵向挂点时的桨毂载荷。当处于同一飞行速度，挂点处于与后挂点纵向相距0.4 m的前挂点时，桨毂载荷最大，约为挂点处于后挂点时的1.2倍。挂点越远离后挂点，桨毂载荷越大，且桨毂载荷与挂点距后挂点的距离呈线性关系，并且这种线性关系在飞行速度50 m/s以内均成立。此外，不同飞行速度下所呈现的线性关系，其斜率几乎不变，均约为9200。

2.2.3 挂点垂向变化对桨毂载荷的影响

当挂点位置只有垂向变化时，对桨毂载荷的影响见图8，此处的本机重心位置处于正常重心，挂点坐标见表2。

可以看出，低挂点的桨毂载荷大于高挂点。低挂点时，吊挂所带来的低头力矩更大，机身低头加剧，这点可以从图9看出。但本机和吊挂整个系统的水平阻力在高低挂点几乎一样，所需旋翼产生的水平分力需一样，故而要求桨盘与水平的夹角也基本一样。在吹风挥舞只随挂点垂向变化而发生微小变化时，为保夹角不随挂点位置改变，在俯仰角不同的情况下，需要周期操纵来调节使其维持不变，图10展现的纵向操纵也是佐证。高挂点纵向向前操纵更大，而吹风挥舞使桨盘后倒，因此高挂点的桨盘合倾角更小，故而桨毂载荷更小。

由上述可知，垂向远离本机重心的低挂点的桨毂载荷较大。为进一步探究挂点垂向至本机重心距离的变化对桨毂载荷的影响，在高、低挂点之间再取了若干挂点，得到了如图11所示的不同速度、不同高度挂点的桨毂载荷。图中距离为0 m表示挂点与本机重心垂向坐标一样；1.2 m表示挂点垂向位置比本机重心低1.2 m。可以看出，在相同速度下，挂点至本机重心垂向距离越大，其桨毂载荷越大，且呈现线性关系，只是不同速度时，线性关系的斜率不同：在飞行速度15 m/s时，斜率为425，挂点位于低挂点的桨毂载荷是高挂点的1.02倍；而当速度达到50 m/s时，两挂点桨毂载荷却为1.18倍，直线斜率为2910。但速度与斜率呈现二次函数关系，具体可见图12。

3 结论

吊挂飞行时，为减少桨毂载荷，提高桨毂使用寿命，挂点位置的选取至关重要。本文基于已有的直升机飞行动力学模型，将吊挂假设为单质点，吊挂系统对直升机的影响等效处理成额外作用力和力矩，组建直升机吊挂飞行动力学模型。然后，针对直升机吊挂系统进行了配平计算，计算结果均与试飞数据吻合。最后，基于该模型，探究了挂点位置对旋翼桨毂载荷的影响。结果表明：

1) 当直升机吊挂系统的总质量与无吊挂本机相同，挂点位于本机重心时，吊挂几乎不会给桨毂带来额外的载荷。

2) 当飞行速度相同，挂点位置只有纵向变化时，桨毂载荷最大时的挂点位置与本机自身特性有关；桨毂载荷随挂点位置纵向变化趋势与无吊挂时桨毂载荷随本机重心纵向变化的趋势一致。

3) 当挂点低于本机重心且只有垂向变化，飞行速度相同时，挂点至本机重心垂向距离越大，其桨毂载荷越大，且呈现线性关系；不同速度的线性关系斜率不同，但斜率与速度呈现二次函数关系。