一题多解下的通性通法研究——一道双曲线问题的解法规律及拓展

安徽 王成功 陈 曦

圆锥曲线是高考的必考问题，尤其是双曲线，在历年高考中双曲线及其性质从未缺席过，在选择题或填空题中必考一题，也时常以解答题的形式来考查.在考试大纲中的要求虽然是了解层次，但是在复习的时候，我们不可忽略其重要性.双曲线问题通常考查的是学生的分析问题和转化问题能力以及计算能力，这也是数学核心素养的综合体现.在考试中，经常因为其计算难度大、条件错综复杂、转化角度多样，而让考生猝不及防甚至束手无策.然而我们知道，在解题中，解无定法，解必有法，只要我们把双曲线的基本性质熟记于心，把握高考命题规律，把不同问题的共性找到，就可以明确解决这类问题的通性与通法.下面就让我们通过对一组典型问题及其变式的一题多解研究，探寻解决双曲线问题的通性与通法，给一线教师和高三学生明确复习目标，使学生在高考中能够轻松应对双曲线问题.

1.试题呈现

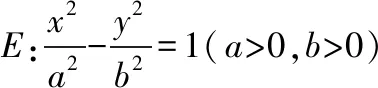
(Ⅰ)求双曲线E的离心率；

(Ⅱ)如图，O为坐标原点，动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、四象限)，且△OAB的面积恒为8，试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程；若不存在，说明理由.

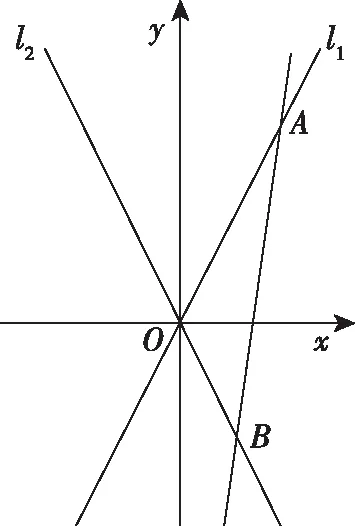
本题是一道典型的直线与双曲线位置关系的问题.对学生的演算能力和逻辑推理能力要求都非常高，乍看上去，让学生感到无从下手，计算量也让人感觉非常害怕.其实解决本题可通过不同的角度来寻找解题突破口，不仅可以从知识上和能力上来提升学生解决问题和分析问题的能力，更是可以从解题方法和思想上给我们提供指导价值.

【方法分析】

(Ⅰ)我们要解决的是求双曲线的离心率，其本质是考查双曲线的标准方程以及系数a,b,c之间的关系，通常可以从设标准方程的角度来思考问题，由于本题给出了双曲线的渐近线，因此，也可以从渐近线方程直接得到系数之间的比例关系.具体做法如下.

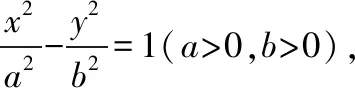
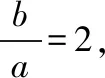
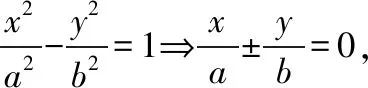
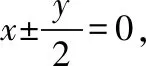
这是两种常见的处理双曲线渐近线方程和标准方程之间关系的途径，在解决问题时可以根据自己的接受能力和学习习惯选择适合自己的一种方式来解题.

(Ⅱ)【思路分析1】这种是从特殊到一般的思维方式，在求关于定值、定直线、定点等问题时，我们可以先考虑特殊情况，找到答案，如果是选择题和填空题，问题迎刃而解，如果是解答题，可以带着结论再证明.

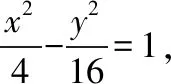
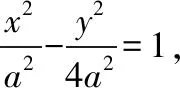
设直线l与x轴交于点C.

当直线l⊥x轴时，由于直线l与双曲线E有且只有一个公共点，则|OC|=a,|AB|=4a，

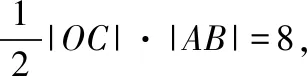
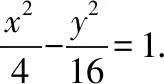
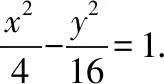
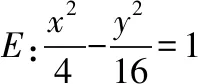
设直线l的方程为y=kx+m，依题意得k>2或k<-2.

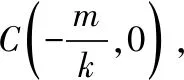
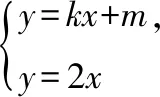
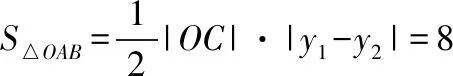
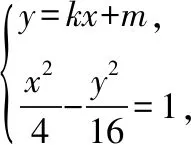
因为4-k2<0，所以Δ=4k2m2+4(4-k2)(m2+16)=-16(4k2-m2-16).

又因为m2=4(k2-4)，所以Δ=0，即直线l与双曲线E有且只有一个公共点.

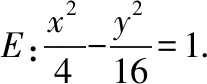
【思路分析2】在解决直线与双曲线位置关系问题时，如果直线斜率可能不存在，为了避免讨论，可以把直线设成x=my+t形式，这样方便处理，而且也给计算带来很大的便捷.

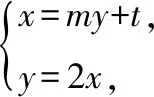
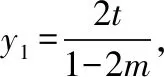
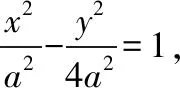
设直线l的方程为x=my+t,记A(x1,y1),B(x2,y2).

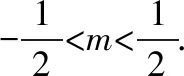
设直线l与x轴交于点C，则C(t,0).

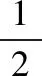
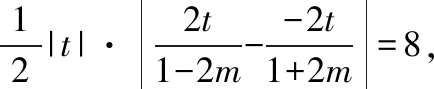
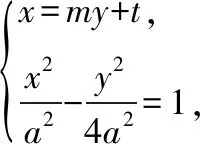
因为4m2-1<0，直线l与双曲线E有且只有一个公共点,当且仅当Δ=64m2t2-16(4m2-1)(t2-a2)=0时满足.

即4m2a2+t2-a2=0，即4m2a2+4(1-4m2)-a2=0.

即(1-4m2)(a2-4)=0，所以a2=4.

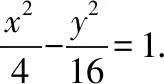
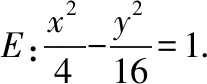
【思路分析3】从直线的斜率存在和不存在，对直线分两种情况进行讨论，计算量大一点，但是这种方式是学生们易于理解的通性与通法，同时展示这种解法的目的在于训练学生解决圆锥曲线问题的能力.

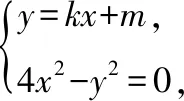
【详解】当直线l不与x轴垂直时，设直线l的方程为y=kx+m，

记A(x1,y1),B(x2,y2).依题意得k>2或k<-2.

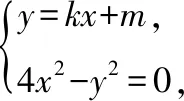
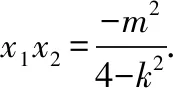
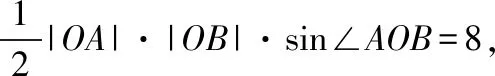
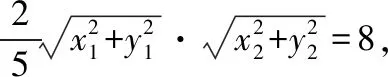
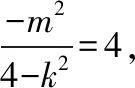
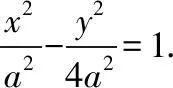
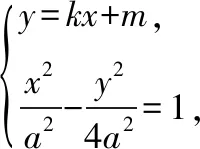
因为4-k2<0,直线l与双曲线E有且仅有一个公共点，当且仅当Δ=4k2m2+4(4-k2)(m2+4a2)=0时满足.

即(k2-4)(a2-4)=0，所以a2=4.

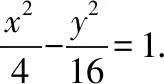
当l⊥x轴时，由△OAB的面积等于8可得l:x=2，

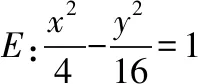
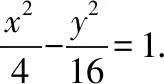
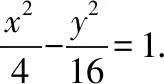
通过本例，我们还可以得到以下几点启示：

(1)通过本例我们知道，高考中双曲线以及直线与双曲线的位置关系问题的主要考查形式有：双曲线的标准方程、离心率、渐近线，过定点的直线与双曲线的交点问题，直线与双曲线的交点和原点、焦点或某定点围成的三角形问题，直线的垂直、向量的数量积等有关问题.

(2)熟练掌握双曲线中系数a,b,c之间的关系，对于直线与双曲线的交点问题，往往是利用韦达定理，设而不求来解决.特别地，对于较简单的问题，也可以直接求出交点来求解.

无独有偶，这类问题不是偶然出现，解题方法也不是只能解决一个问题，而是可以解决与双曲线有关的一类问题，解题思想可以拓展到解决整个圆锥曲线问题.

2.同类问题的不同呈现，解决问题的通性通法

对于双曲线问题中，涉及直线与双曲线的位置关系时，需要解决的问题可以是通过不同的设问来呈现的，这类问题需要通过分析题设和问题之间的内在联系，把需要解决的问题转化成联立直线方程与双曲线方程，设而不求的方法来求距离、斜率、方程等问题.

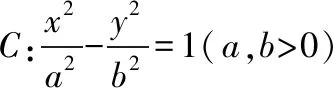
(Ⅰ)求C的离心率；

(Ⅱ)设C的右顶点为A，右焦点为F，|DF|·|BF|=17，证明：过A，B，D三点的圆与x轴相切．

【精彩解答】

(Ⅰ)解法一：根据直线过(1,3)，求出直线方程，再把直线带入双曲线方程，利用韦达定理和中点坐标公式即可求出系数a,b的关系式，进而求出离心率.

【详解】由题设知，l的方程为y=x+2.把直线带入双曲线方程，

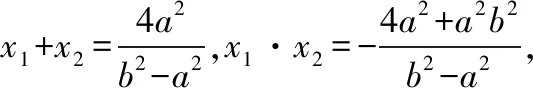
解法二：设出B，D两点坐标，利用点差法结合直线的斜率和中点坐标，得出系数a,b的关系式，进而求出离心率.

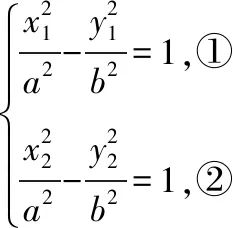
【点评】点差法是处理直线与圆锥曲线相交弦的中点和相交弦的斜率问题的常用方法，直接设点代入方程再作差，可以整体考虑中点和斜率之间的关系，从而起到简化运算过程的效果，这种方法可以解决一类特殊问题.

(Ⅱ)解法一：根据离心率设出双曲线方程，联立直线和双曲线方程，利用韦达定理以及两点间距离公式求出|BF|，|FD|，|BD|，再利用|BF|·|FD|=17，求出双曲线方程，结合|MA|的长度即可证明结论.

【详解】由(Ⅰ)可知，C的方程为：3x2-y2=3a2，如图所示：

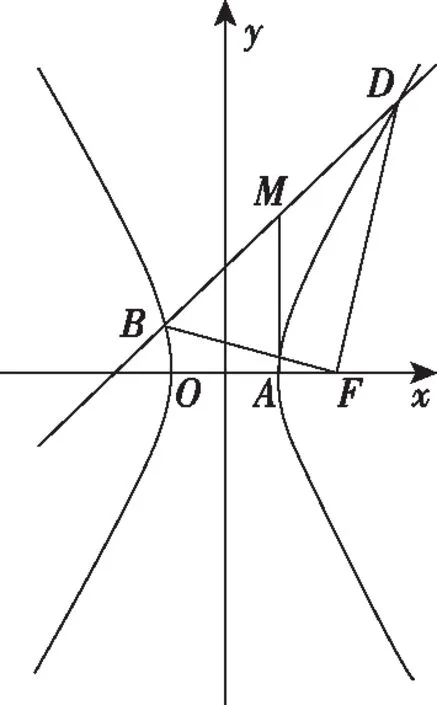
故不妨设x1≤-a，x2≥a，

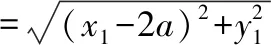
=2x2-a，

|BF|·|FD|=(a-2x1)(2x2-a)=-4x1x2+2a·(x1+x2)-a2=5a2+4a+8,

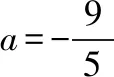
连接MA，则由A(1,0),M(1,3)知，MA⊥x轴，且|MA|=3，从而MA=MB=MD，因此以M为圆心，MA为半径的圆经过A,B,D三点，且在点A处与x轴相切.所以经过A,B,D三点的圆与x轴相切.

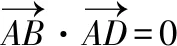
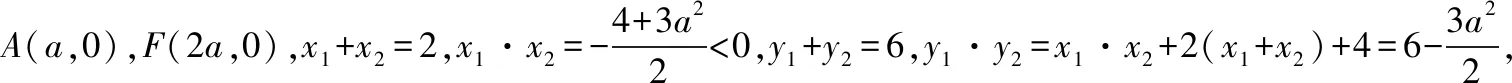
故不妨设x1≤-a，x2≥a，

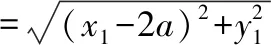
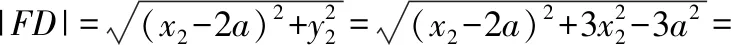
|BF|·|FD|=(a-2x1)(2x2-a)=-4x1x2+2a(x1+x2)-a2=5a2+4a+8，

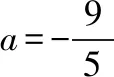
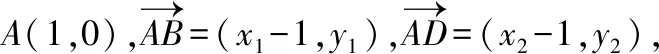
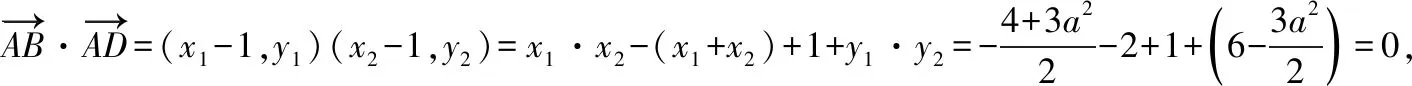
所以△ABD是直角三角形，那么经过A,B,D三点的圆的圆心为BD中点M，

又xM=xA=1，所以可知该圆与x轴相切，切点为A.

【点评】第二问要解决的问题，第一眼看上去会让我们感觉没有任何方向，这时候我们要回到圆锥曲线问题考查的方向和目的上来，这样就会把问题与距离或者是直线联系起来，进而找到解决问题的突破口.

3.方法和思想的延续性

例题所呈现的分析问题和解决问题的思想方法不仅仅可以解决双曲线问题，还是所有圆锥曲线问题的缩影，解决圆锥曲线的问题都可以从不同的角度来探寻解题突破口，从而让我们的复习达到事半功倍的效果.

【变式2】在平面直角坐标系xOy中，对于直线l：ax+by+c=0和点P1(x1,y1),P2(x2,y2)，记η=(ax1+by1+c)(ax2+by2+c).若η<0，则称点P1,P2被直线l分隔，若曲线C与直线l没有公共点，且曲线C上存在点P1，P2被直线l分隔，则称直线l为曲线C的一条分隔线.

(Ⅰ)求证：点A(1,2)，B(-1,0)被直线x+y-1=0分隔；

(Ⅱ)若直线y=kx是曲线x2-4y2=1的分隔线，求实数k的取值范围；

(Ⅲ)动点M到点Q(0,2)的距离与到y轴的距离之积为1，设点M的轨迹为曲线E，求证：通过原点的直线中，有且仅有一条直线是E的分隔线.

【精彩解答】

(Ⅰ)解法一：把点A1,2，B-1,0带入η=ax1+by1+cax2+by2+c，即可证明.

【详解】把点A(1,2)，B(-1,0)带入η=(ax1+by1+c)(ax2+by2+c)，因为η=-4<0，所以点A,点B被直线x+y-1=0分隔.

【点评】本题涉及新定义问题，遇到这类题，先理解定义，只需要找到确保结论成立的条件即可，不必想着定义是否正确，定义是否符合逻辑.因为这类问题一般是高等数学的渗透，其正确性是毋庸置疑的，我们只需要考虑应用我们所学的高中知识进行解题，并把结论进行适当推广即可.

解法二：由题意可知，两点被直线分隔即两点在直线的两侧，再带入点直接验证.

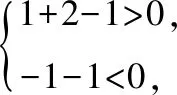
【点评】这是严格按新定义证明的一种方法，也是解决新定义问题的通法.

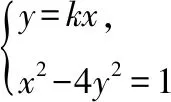
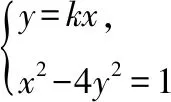
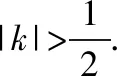
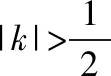
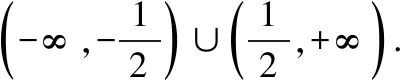
【点评】这种方法需要借助于数形结合思想，会更加直观地得到结论.

解法二：根据分割线定义，只需要满足两个条件：一是直线和曲线没有公共点，即对应方程组无解，二是存在两点在直线两侧.

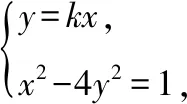
又曲线x2-4y2=1上显然存在点(-1,0)和(1,0)满足η=-k2<0.

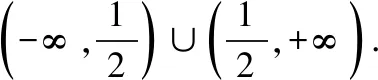
(Ⅲ)解法一：设M的坐标为(x,y)，分过原点的直线不是y轴和是y轴两种情况来证明.

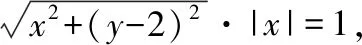
对任意的y0，(0,y0)不是上述方程的解，即y轴与曲线E没有公共点.又曲线E上的点(-1,2)和(1,2)对于y轴满足η<0，即点(-1,2)和(1,2)被y轴分隔.

所以y轴为曲线E的分隔线.

若过原点的直线不是y轴，设其为y=kx.

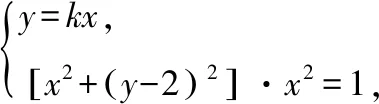
得[x2+(kx-2)2]·x2-1=0，

令f(x)=[x2+(kx-2)2]·x2-1，

因为f(0)·f(2)=(-1)[16(k-1)2+15]<0，所以方程f(x)=0有实数解.

即直线y=kx与曲线E有公共点，故直线y=kx不是曲线E的分隔线.

综上可得，通过原点的直线中，有且仅有一条直线是E的分隔线.

【点评】通过分析，直线只需要分过原点的直线不是y轴和是y轴两种情况讨论即可，这是在对题意深入分析后，我们可以走的一些计算上的捷径.

解法二：设M的坐标为(x,y)，根据M到点Q(0,2)的距离与到y轴的距离之积为1求出轨迹方程，然后对过原点的直线分斜率存在和斜率不存在两种情况进行分析证明.

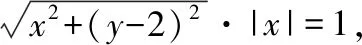
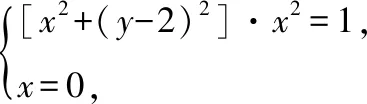
下证：斜率存在时直线与曲线都有交点.

设直线方程为y=kx，

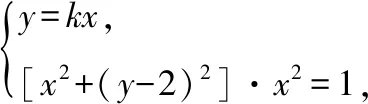
易得[x2+(kx-2)2]·x2-1=0，关于x的方程无论k为何值，必有解.

综上可得，通过原点的直线中，有且仅有一条直线是E的分隔线.

【点评】通性通法，涉及直线与圆锥曲线的位置关系，需要考虑直线的斜率存在和不存在时，分类讨论解决，在解决定值问题或者需要证明一个一般性结论问题的时候，可以先考虑特殊情况，通过特殊情况，确定结论，进而再证明一般性结论.

通过以上这些典型问题的分析和解决，虽然提供给大家的是解决双曲线问题和直线与双曲线位置关系问题的通性通法，但目的是可以把解题的思想方法用来解决所有圆锥曲线问题.圆锥曲线问题的考查角度全面，主要考查学生对定义的理解、对性质的应用、考查计算能力以及转化问题的能力.对学生们而言，普遍认为圆锥曲线第一问都会做，从而忽略第一问的巧解，巧解一般都是借助于性质、数形结合思想或者是定义，减少计算量，在考试时候，能够节约大量的时间，有的同学虽然能够解决第一问，但是花费了大量的时间去解方程组，计算能力弱的同学往往直接导致错误，这些都是不可取的.所以第一问的解决，一般都提供一种基本方法和一种巧解方法.第二问的解决方法较为灵活，我们需要的是“见什么病抓什么药”，从问题入手，结合一般解题思想，寻找解决问题的突破口，对于复杂的问题或者是问法不太常见的问题，需要通过对题设条件全面的分析，把问题转化成常规的求距离、求斜率、求直线或者是求曲线方程等问题后再解决.