低频线谱激励下动力吸振器设计研究

贺辉雄，向 阳，张 波

（1.武汉理工大学 高性能船舶技术教育部重点实验室，武汉430063；2.武汉理工大学 能源与动力工程学院，武汉430063）

辅机设备振动引起船体振动，进而通过介质水将振动能量以声辐射的形式传播出去，影响舰艇行驶过程中的机械设备的安全运行、人员舒适性及舰船声隐身性。目前船舶主机设备的减振降噪措施已十分成熟，而针对辅机设备激励下船体的减振降噪相关研究相对较少，且集中在加强船体结构[1]及铺设吸声材料[2]方面。而作为解决低频振动控制的有效途径之一，动力吸振器可以通过转移并衰减船体振动能量起到抑制辅机设备激励下船体振动的作用[3]，有利于减小船体对外的声辐射水平。

动力吸振器在振动控制领域应用十分广泛，杜勇[4]介绍了动力吸振器的设计方法，针对汽车悬架系统设计被动式动力吸振器参数并通过仿真计算确定其吸振性能；张龙庆[5]通过定点理论及多自由度系统等价质量识别法确定浮置板轨道附加动力吸振器的最优参数及最优安装位置；王文初[6]针对船舶管路系统的低频线谱和三向振动的特点，并基于结构阻抗分析法设计了一款新型悬臂梁式动力吸振器；卢坤[7]针对船舶推进轴系纵振设计了基于磁流变弹性体的半主动动力吸振器。动力吸振器在汽车、土建等领域应用广泛，在船舶领域应用主要集中在船舶轴系、管道等方面，而针对船体减振降噪设计吸振器案例几乎没有，因此，有必要开展船体附加动力吸振器设计研究。

本文主要针对包含辅机设备在内的船舶舱段模型来设计动力吸振器吸振方案，包括以下内容：建立双层底仿真模型作为研究对象模拟船舶辅机运行过程中船体振动噪声水平，进行谐响应分析，确定吸振频率；识别该原点传递函数，得到主系统等效参数；根据得到的主系统等效参数，采用定点理论设计动力吸振器，探究吸振器质量及数量对双层底模型吸振效果的影响规律；设计针对该模型的最终吸振方案，并采用ANSYS与Virtual Lab软件分析其振动及噪声水平。

1 动力吸振器设计流程

文献[8]详细介绍了单自由度系统附加动力吸振器设计流程，而作为本文研究对象，双层底模型是一个连续体系统，无法直接采用该文献中给出的单自由度定点理论来设计动力吸振器，但可以将该连续体系统离散为多自由度系统，并在无模态耦合条件下将多自由度系统当成多个单自由度系统的集合进行处理[5]。因此，针对双层底模型设计动力吸振器时，可以利用模态参数识别方法建立单自由度系统的集合构成的非耦合模型，从而将连续体模型简化为多个单自由度系统模型，并根据单自由度系统的动力吸振器设计方法来进行抑振设计。

1.1 模态参数识别

通过模态参数识别，将双层底模型等效为单自由度系统，并建立主系统等效模型。主系统等效参数包括：等效质量、等效刚度及等效阻尼。对于这3个主系统等效参数，只需要求得安装位置处主系统的原点传递函数，并通过曲线拟合手段识别该位置处主系统固有频率及对应的等效质量，就可以推算出其等效刚度和等效阻尼。

基于模态参数识别的主系统单自由度等效模型建立流程如下：

(1)基于ANSYS 有限元软件，求取安装点处主系统原点传递函数。

(2)确定待减振频率段。

(3)建立单自由度目标函数模型。

(4)借助基于MATLAB软件的有理分式曲线拟合法识别主系统的等效参数，将其等效为单自由度系统。

根据模态参数识别方法[9]，编写MATLAB 有理分式多项式曲线拟合程序，通过拟合得到的吸振器待安装点的原点传递函数表达式，推导主系统等效参数，推导过程如下。

通过MATLAB 曲线拟合程序识别得到的原点传递函数

其中，分子C(s)、分母D(s)均为有理分式多项式，N为分析频段内模态阶数，ak、bk分别为C(s)与D(s)的有理分式多项式系数。

通过求取原点传递函数极点来确定主系统固有频率，可令分母D(s)=0，即

解上式，可求出N对复根Sr和Sr*，即

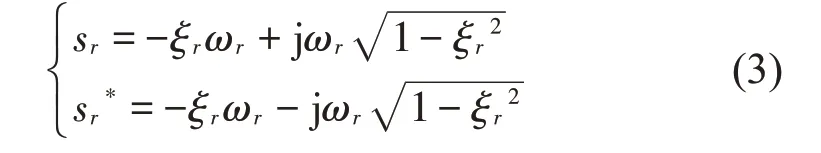
由此可推出第r阶固有频率ωr和阻尼比ξr

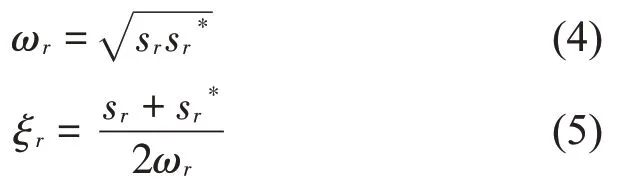
原点传递函数H(s)的r 阶留数为A(r)，根据留数定理

可推导出传递函数分量表达式

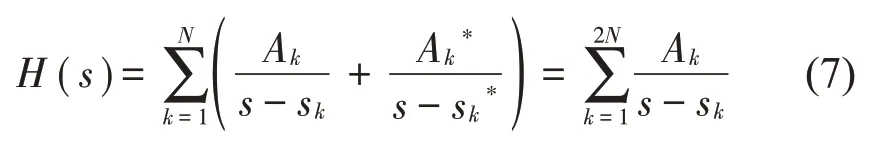
理论上各阶留数为纯虚数，而由于存在运算的截断误差，使留数有很小的实部。因此，仅取留数Ar的虚部来识别各阶等效参数，其中r 阶固有频率处模态质量、模态刚度、模态阻尼计算公式如下

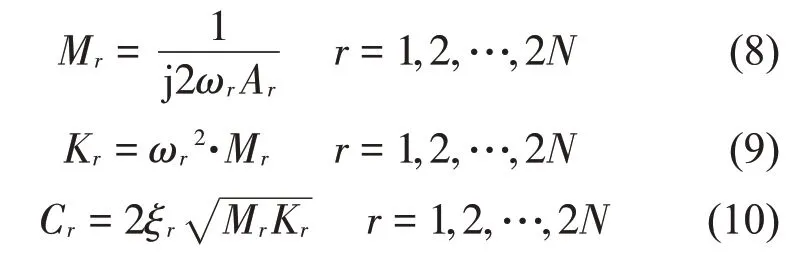
通过上述识别过程得到等效参数，从而可以建立该模态频率处主系统单自由度系统等效模型。

1.2 动力吸振器最优参数设计方法

根据模态参数识别得到的主系统第r 阶固有频率处等效质量Mr、等效刚度Kr、等效阻尼比ξr，利用文献[5]中单自由度有阻尼主系统定点理论，可求取动力吸振器的最优参数如下：

(1)动力吸振器最优质量

(2) 动力吸振器最优刚度

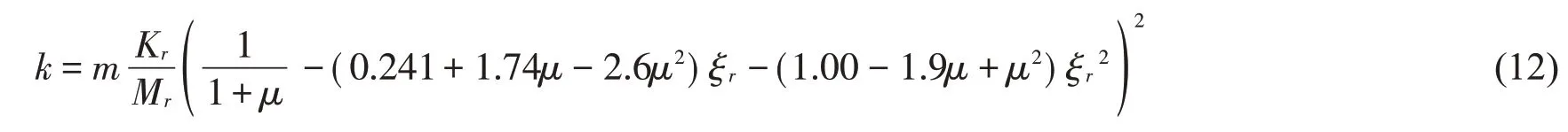
(3) 动力吸振器最优阻尼

式(11)至式(13)中μ 为动力吸振器与主系统质量比。

2 船舶双层底模型吸振方案设计

2.1 双层底有限元建模

为了设计附加在双层底模型上的动力吸振器，基于HyperMesh 软件建立船舶双层底有限元模型。模型主体材料为钢材，弹性模量E=2.1×1011Pa、密度ρ=7 850 kg/m3、泊松比μ=0.3。该模型主要由内底板、外底板、实肋板、3 个基座、18 个加强筋组成，板结构及基座采用shell181 单元模拟，加强筋采用beam188单元模拟。由于整条船舶尺寸过大及后续实验条件限制，本文建立的双层底模型仅为所截取的部分船体，而为模拟船舶在水中运行情况，模型底部采用4 个3 向弹簧支撑，3 向弹簧由combine14 单元模拟，弹簧单元底部节点全约束。由于离心泵结构复杂且对双层底模型固有属性影响较大，故将其等效为一质点，其质量为离心泵实际质量即231.7 kg，并与基座上3个机脚节点刚性连接。同时，为解决弹性波在双层底模型截断处无法传播的问题，需要建立弹性波无反射边界条件，故在模型四周采用沙箱约束，沙箱采用solid45 单元模拟，其材料参数取为弹性模量E=4×107Pa、密度ρ=1500 kg/m3、泊松比μ=0.25，由于沙土为非线性材料，故需设置Drucker-Prager 准 则，其 参 数 为Cohesion=0、Fric Angle=20、Flow Angle=20。建立的双层底有限元模型如图1 所示，图a 为双层底全约束模型，图b 为双层底部分约束模型（为便于观看细节，特意隐藏沙箱部分）

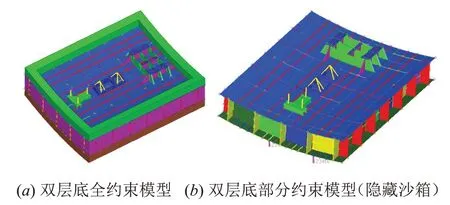
图1 双层底三维有限元模型

同时，为模拟双层底模型附加的动力吸振器，基于HyperMesh 软件建立动力吸振器有限元模型，采用mass21 单元模拟吸振器的质量，采用combine14单元来模拟吸振器的刚度及阻尼，图2 即为单个吸振器的有限元仿真模型。

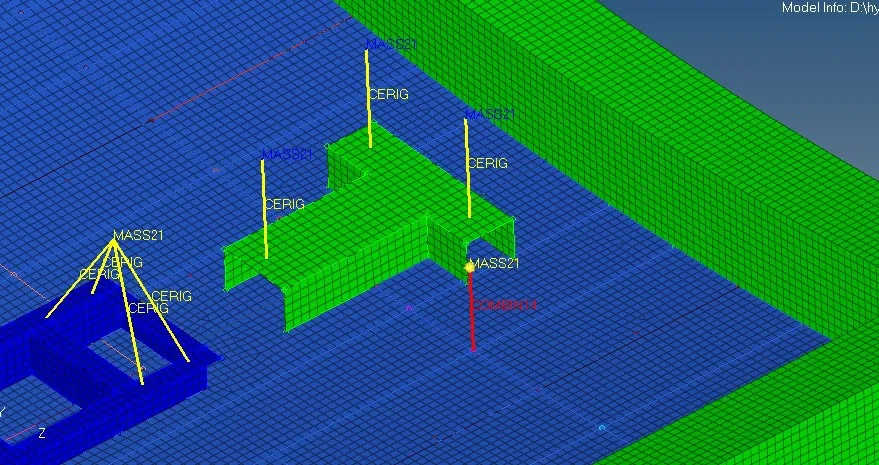
图2 单个吸振器的有限元仿真模型

通过建立动力吸振器仿真模型，可以分析吸振器质量及布置数量对吸振器效果的影响，便于更好地确定双层底模型的吸振方案。

2.2 双层底模型振动噪声评价指标

动力吸振器的主要设计目标在于减小双层底结构的振动响应及外底板对外的辐射噪声水平，故需要设定评价指标来衡量该模型振动及噪声水平，进而评价动力吸振器的吸振效果。在本文中结构振动响应水平的评价指标有2 个：一是模型各节点吸振频率处频率响应曲线峰值，二是外底板垂向振动烈度。结构对外辐射噪声水平的评价指标为外底板辐射声功率。

由于双层底结构节点数过多，为准确反映该模型局部振动响应情况，先于双层底结构内底板和外底板上选取若干评价点，通过求解其位移响应幅值来反映模型振动水平，选取的评价点位置、编号信息如图3所示。

图3 双层底评价点位置示意图

2.3 动力吸振器安装位置选择

根据文献[9]中相关结论，动力吸振器应安装在响应幅值点上，因此需要通过仿真计算求取模型的位移响应极值点来确定动力吸振器的安装位置。首先，对双层底模型进行谐响应分析，求解各节点处位移响应，确定吸振频率，然后提取模型在该频率处位移响应云图，并根据响应云图确定吸振器的安装位置。在谐响应分析前，需要施加外部激励，由于本文研究对象是辅机设备激励下双层底模型的振动噪声，故选取船用离心泵作为激励源。

通过实验测得额定工况下离心泵机脚处加速度响应数值，将其作为外部加速度激励，施加到双层底有限元模型离心泵机脚节点上，施加方向为垂直离心泵基座方向。离心泵3个机脚处施加的加速度曲线如图4所示，施加的节点位置如图5所示。

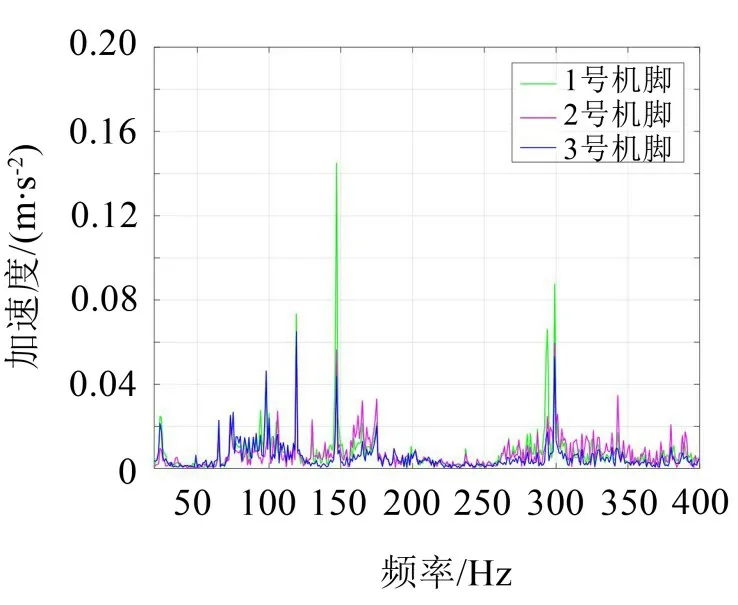
图4 施加在3个机脚处的加速度激励曲线

施加加速度激励后，通过谐响应分析可以得到双层底模型中各评价点的位移响应曲线，由于这里主要关心的是模型的垂向振动，文中位移响应幅值方向均取垂直于离心泵基座方向。依次求解双层底结构内、外底板节点1－39的响应，列出代表性的1、2、3、4评价点位移频率响应曲线（纵坐标为位移，单位是mm），如图6所示。

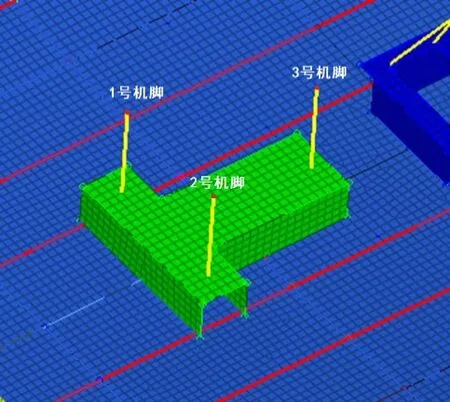
图5 机脚位置示意图

由图6 可以看出，各点处位移响应幅值主要集中在33 Hz处。33 Hz为双层底模型的固有频率，该频率处模型产生强烈振动，位移响应幅值为20 Hz～400 Hz频率范围内的位移响应最大值。因此可以通过针对33 Hz频率设计动力吸振器来达到抑制结构振动的目的。在机脚加速度激励下，双层底结构33 Hz频率处的响应云图如图7所示。

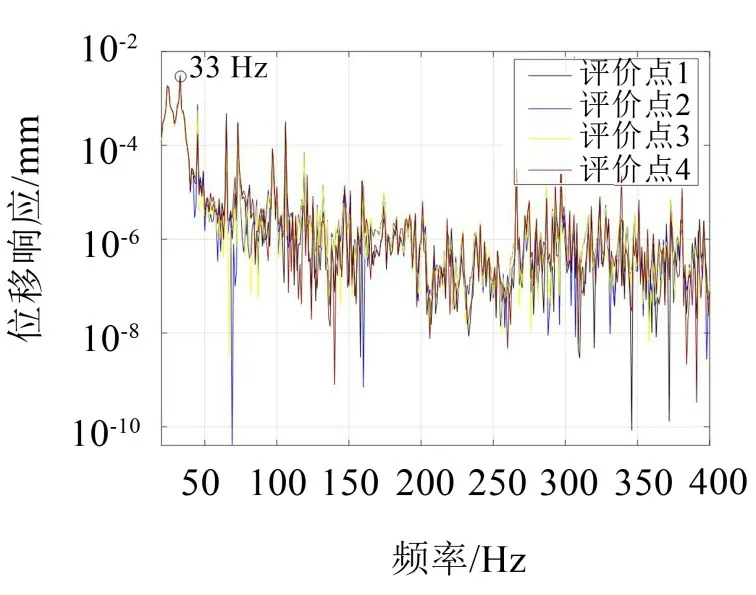
图6 1－4评价点频率响应曲线

从图7不难发现，33 Hz频率处双层底模型位移响应峰值位于离心泵一侧的双层底模型端部，并沿着图示长度方向位移响应幅值逐渐减小并降至0，然后略有增大。

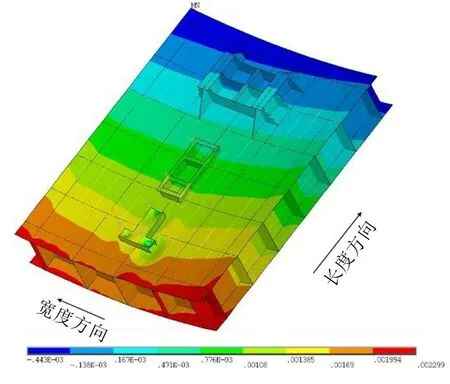
图7 双层底模型33 Hz处的响应云图

根据响应云图，在内底板上选取位移响应尽可能大的节点作为动力吸振器的安装位置。同时，考虑到沙箱的存在及吸振器的尺寸，选取节点176 271、190 020、45 313、36 877 作为吸振频率为33 Hz的吸振器安装位置，节点位置如图8所示。

图8 吸振器安装位置示意图

2.4 动力吸振器最优参数设计

在针对33 Hz 频率设计动力吸振器时，先利用ANSYS 有限元软件计算所选安装节点的原点传递函数，将以上数据代入MATLAB 模态识别程序，对以上频响函数进行有理分式曲线拟合，得到拟合前后曲线及误差值曲线（图11 所示为176 271 节点处拟合前后曲线及误差值曲线）。从图9 可以看出176 271节点处曲线拟合效果较好，误差值可以忽略不计。根据拟合后原点传递函数及式(1)至式(10)，可以计算得到该节点处固有频率fr=32.7837 Hz，主系统等效质量Mr=2 598.35 kg ，等效刚度Kr=110 248 660.36 N/m，等效阻尼比ξr=0.001，将Mr、Kr、ξr代入式(11)至式(13)中，在吸振器质量给定的条件下，可以求得该节点处动力吸振器刚度、阻尼参数。

基于以上方法，设计出的双层底模型各节点处的动力吸振器在不同质量条件下的最优参数如表1所示。

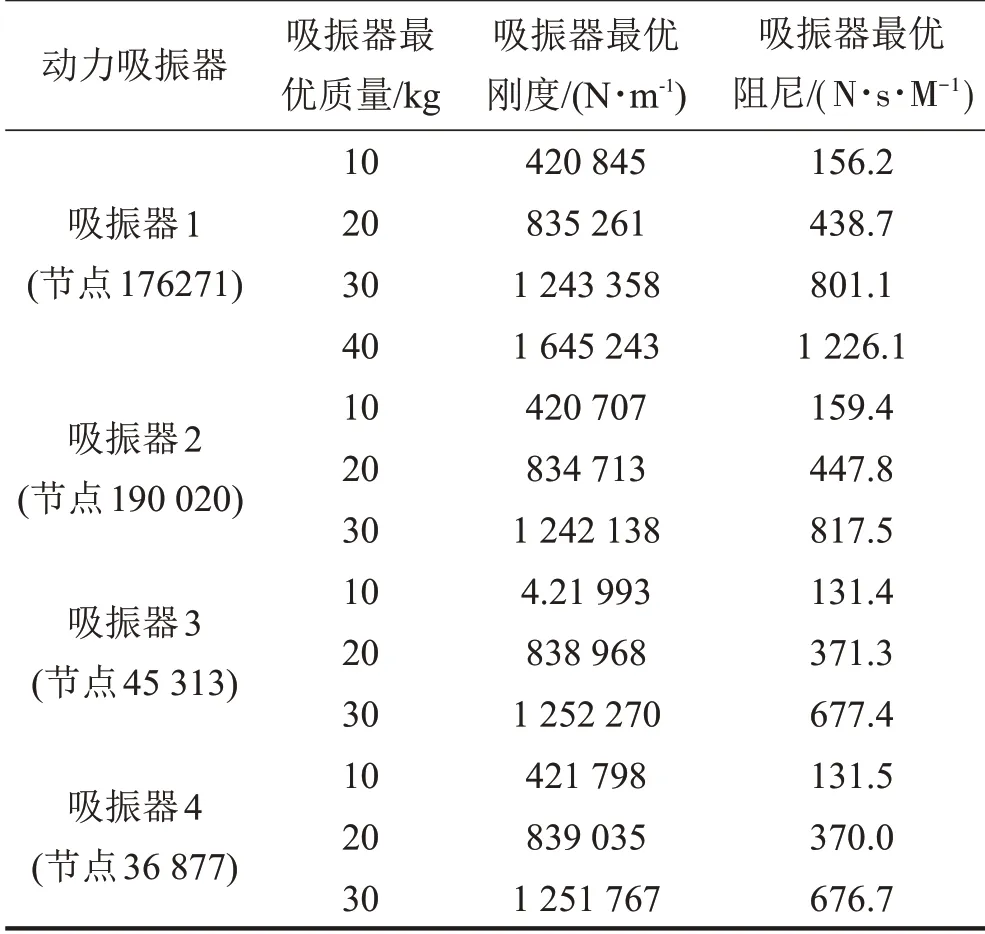
表1 各安装位置动力吸振器最优参数

2.5 吸振质量对吸振效果的影响

理论上，增加动力吸振器与主系统质量比，可以提高吸振效果，但是会使整个结构变重。为了避免增加过多的质量，通常将质量比限制在0.1 以下，对于主系统较大的情况，甚至通过动力吸振器的小型化将质量比控制在0.01[10]。由于主系统质量为2 318 kg，考虑到质量、尺寸的限制，动力吸振器质量仅在0～30 kg内考虑，利用谐响应分析，分别计算质量m=10 kg、20 kg、30 kg 条件下吸振器1 安装在176 271 节点处的位移响应，此时质量比μ 分别为0.004 3、0.008 6、0.012。

提取不同动力吸振器质量下双层底模型各评价点振动位移响应峰值，如图10 所示，坐标轴横轴是各评价点编号，纵轴为30 Hz～40 Hz 内位移响应峰值。

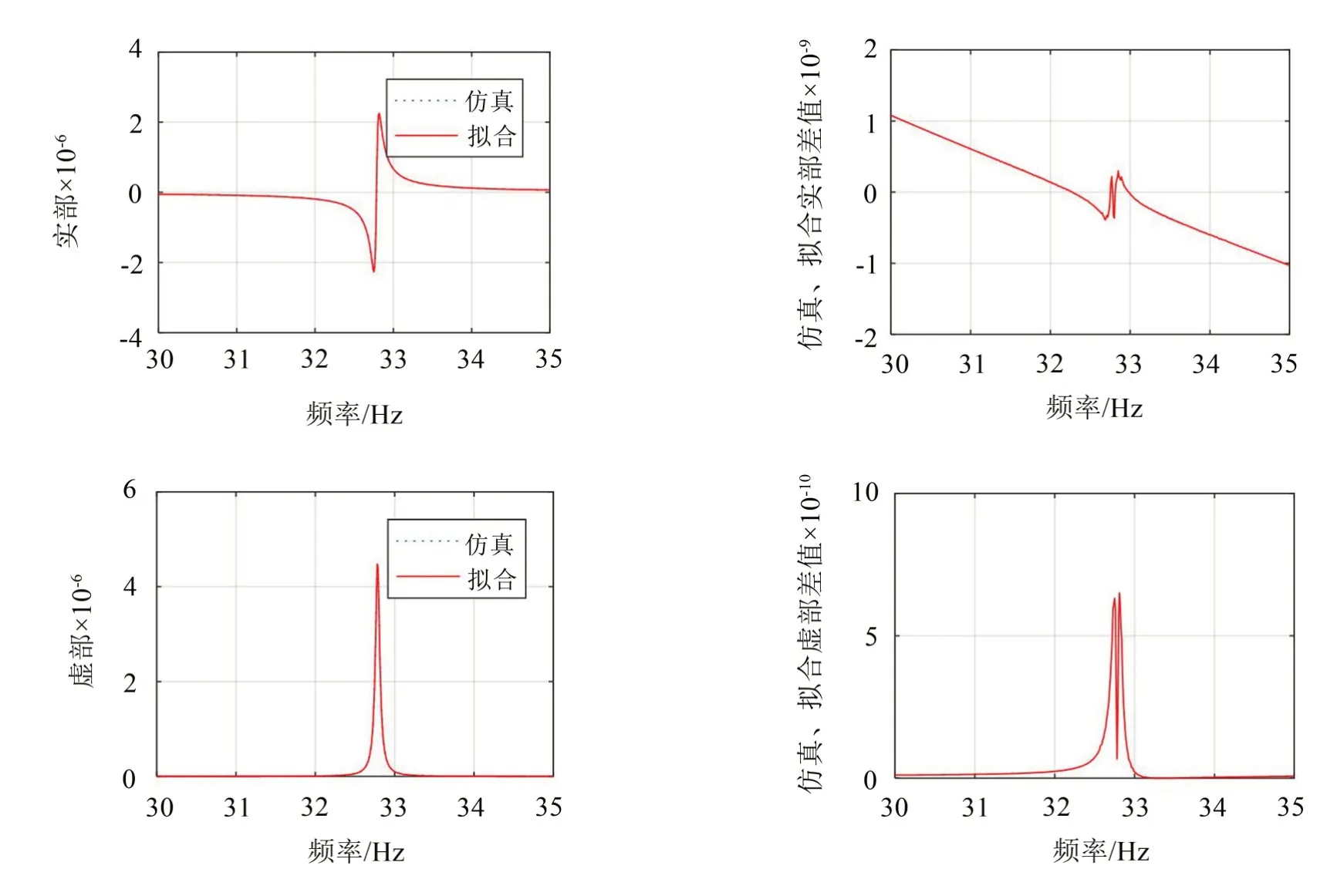
图9 原点传递函数曲线、MATLAB拟合曲线

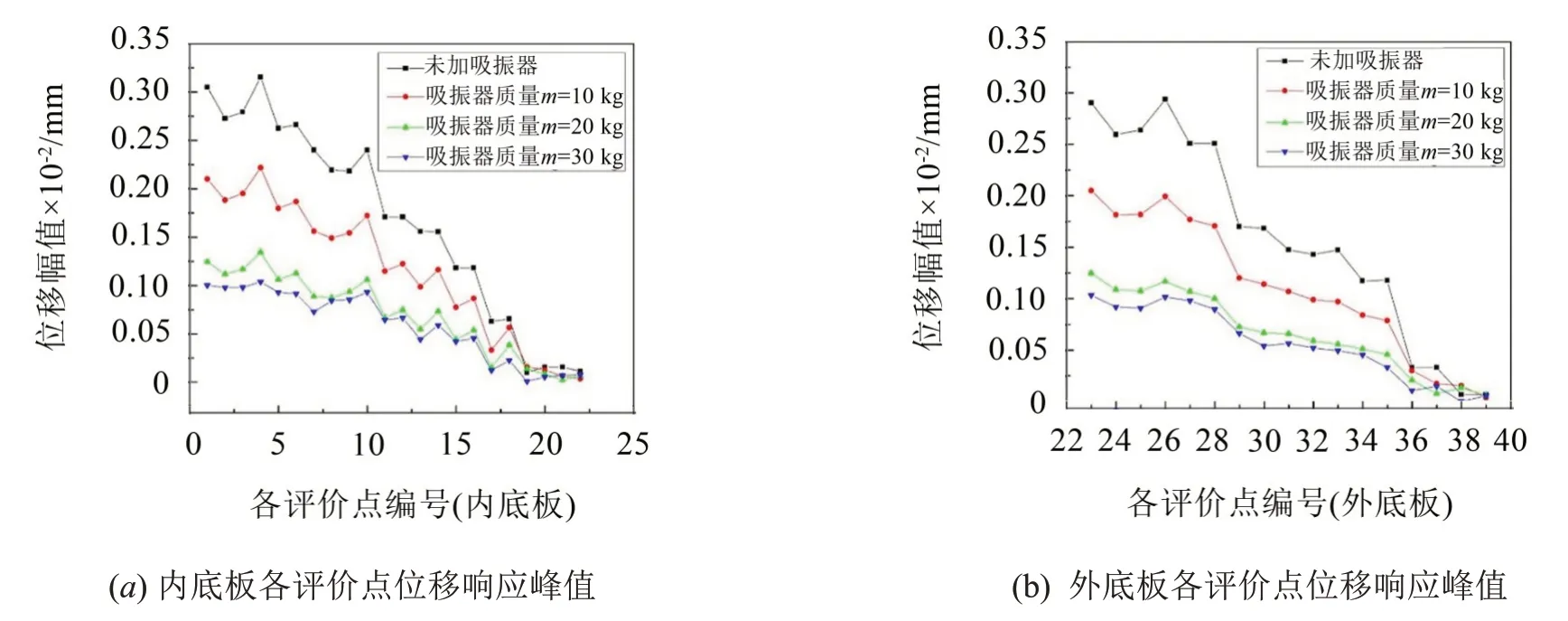
图10 不同吸振器质量工况下内外底板各评价点位移响应峰值

从图10 可以看出，随着吸振器质量的增加，双层底模型各评价点在30 Hz～40 Hz内位移响应峰值逐渐减小，但减小的幅度不同，动力吸振器吸振效果也有所差异。吸振频率为33 Hz 时，当动力吸振器质量逐步增大时，吸振效果显著增加，但当吸振器质量增加到30 kg时，吸振效果变化较小。故为在附加质量较小条件下获得更好的吸振效果，动力吸振器的质量应取为20 kg。

2.6 安装数量对吸振效果的影响

为分析质量一定条件下，动力吸振器安装数量对吸振效果的影响，设置以下3组试验方案：方案1：仅布置吸振器1（m=40 kg）；方案2：布置吸振器1、吸振器2（m=20 kg）；方案3：布置吸振器1、吸振器2、吸振器3、吸振器4（m=10 kg）。以下分别研究这3种方案的吸振效果。

通过谐响应分析，得到各方案在30 Hz～40 Hz各评价点处位移响应峰值，如图11所示。

从图中可以看出，在动力吸振器总质量一定条件下，该双层底模型附加动力吸振器个数越多，吸振效果越好。

2.7 船舶双层底模型动力吸振器实施方案

综合以上分析，针对舱段模型33 Hz 频率处的总体吸振方案为：在内底板上安装共计4个吸振器，分别位于节点176 271、190 020、45 313、36 877 处，该方案有限元模型如图12所示。

各动力吸振器参数如表2所示。

3 双层底模型动力吸振器实施方案吸振效果分析

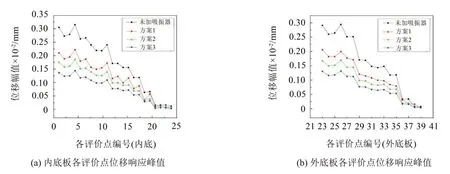
图11 吸振器数量不同时内外底板各评价点位移响应峰值

表2 最终布置方案中吸振器参数

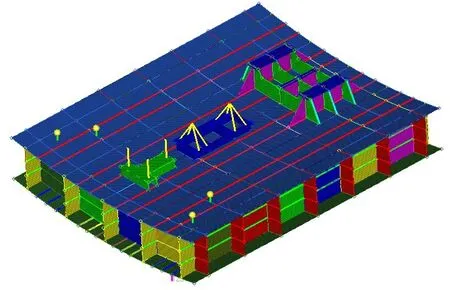
图12 布置吸振器后双层底有限元模型

针对以上双层底模型动力吸振器实施方案，分别考察该模型吸振前后外底板振动及辐射噪声。采用有限元软件ANSYS进行谐响应分析，提取吸振前后外底板各节点速度响应并计算其烈度，如图13所示。

图13 布置吸振器前后双层底外底板振动烈度曲线

可以看出，外底板振动烈度在20 Hz～60 Hz 内有显著减小，其中在33 Hz 处振动烈度数值从3.870×10-4m/s 降至4.126×10-5m/s，降低幅度为89%，而在60 Hz～400 Hz内无明显变化。

模型的声辐射分析在LMS Virtual Lab 中进行，采用Virtual Lab中的间接边界元法进行远场辐射声压的计算。首先把根据有限元谐响应计算得到的舱段外板结构节点振动响应作为位移边界条件映射到声学边界元网格中，并在边界元网格内表面设置声压为0 的声学边界条件，边界元外表面设置流体为空气，然后再进行声学计算。Virtual Lab 模型及模型树如图14 所示。计算后得到吸振前后双层底模型外底板向外辐射声功率曲线如图15所示。

图14 Virtual Lab模型及模型树示意图

根据外底板辐射声功率数据，计算得到吸振后舱段外底板20 Hz～60 Hz内合成辐射声功率级相对于吸振前降低了9.55 dB。同时，从图15 可以看出，安装动力吸振器后，33 Hz频率处的辐射声功率级从72.64 dB降为49.62 dB，降低幅度为23.02 dB。吸振器对双层底外底板辐射噪声的控制效果主要体现在20 Hz～60 Hz 频率范围内，结果表明本文设计的双层底模型动力吸振器能有效抑制外底板20 Hz～60 Hz内声辐射水平。

图15 吸振前后外底板辐射声功率级曲线

4 结语

针对双层底模型设计动力吸振器并分析离心泵运行激励下动力吸振器对双层底模型的吸振特性。经过仿真试验得到的结论如下：

(1)本文基于模态参数识别及定点理论，针对双层底模型设计的动力吸振器具有良好的抑振效果，在33 Hz 频率处振动烈度、辐射声功率均有较大程度降低。同时，20 Hz～60 Hz 内合成辐射声功率级相对于吸振前降低了9.55 dB。

(2)双层底模型附加动力吸振器质量越大，吸振效果越明显，抑制模型振动作用越好。但是随着质量的增加，吸振效果增强的幅度逐渐变缓。

(3)保持吸振器质量不变，增加吸振器个数并设置合理的安装位置会增强动力吸振器对双层底模型的吸振效果。