VS-MFxLMS算法及其在汽车车内噪声有源控制中的应用
张 帅,王岩松,张心光,李文武
(上海工程技术大学 汽车工程学院,上海201620)
随着汽车技术的发展和汽车行驶速度的提高,汽车NVH(Noise,Vibration,Harshness)问题越来越引起消费者的关注。车内噪声是汽车NVH 的核心问题之一,会直接影响车上乘员的乘坐舒适性和身心健康,提高发生汽车事故的概率[1]。
汽车车内噪声的控制方法主要包括被动控制方法[2–3]和有源控制方法[4–5]。被动噪声控制方法是利用声学材料或消声结构来抑制噪声,对中高频噪声特别是高频噪声有较好的效果,但对低频噪声抑制效果不佳。与被动噪声控制方法相比,有源噪声控制方法可以有效抑制低频噪声,并且有系统体积小、便于安装和轻量化设计等优点,已被广泛应用于汽车车内的噪声控制[6–7]。
在车内噪声有源控制方法中,噪声有源控制算法的研究是关键。基于维纳滤波推出的最小均方算法(Least Mean Square,LMS)因其具有算法结构简单、计算量小和鲁棒性强等优点,被广泛应用于汽车车内噪声的有源控制。如冯[8]等采用LMS算法对制动噪声进行有源控制,并取得较好的效果;为了改善传统LMS 算法不能同时提高算法收敛速度和降低稳态误差的缺陷,余[9]和Guo[10]等分别提出了汽车内部噪声主动控制变步长LMS(Variable Step-size LMS,VS-LMS)算法。但LMS 算法以及VS-LMS 算法未考虑到噪声有源控制系统中次级通路存在的影响,会造成车内噪声有源控制系统的稳定性变差。而滤波LMS算法(Filtered-x LMS,FxLMS)考虑了次级通路的影响,具有更好的实用性[11]。与VS-LMS算法类似,文献[12]基于反正切函数提出了一种VSFxLMS 算法,但该变步长方法还存在着算法收敛速度易受到输入信号功率影响的问题,为保证最大输入信号功率的收敛速度,必须牺牲输入信号功率低时的收敛速度;文献[13]提出了一种基于输入信号功率归一化的变步长方法可以有效改善这一问题。文献[14]提出一种改进FxLMS (modified FxLMS,MFxLMS)算法,与FxLMS算法相比,MFxLMS算法具有更好的收敛性能和稳定性[15],但VS-MFxLMS算法还不多见。
本文结合反正切函数和归一化方法,提出了一种新的变步长方法,并依据该方法提出一种VSMFxLMS 算法。采集了汽车车内乘员耳侧噪声,并应 用VS-MFxLMS 算 法、MFxLMS 算 法 和VSFxLMS 算法对采集的汽车车内噪声进行有源控制仿真实验。噪声有源控制的结果表明VS-MFxLMS算法解决了MFxLMS 算法不能同时提高算法收敛速度和降低稳态误差的缺陷;且与VS-FxLMS 算法相比,VS-MFxLMS 算法对车内噪声有源控制具有更好的效果。
1 FxLMS算法
FxLMS算法在LMS算法基础上进行改进,其结构如图1所示。

图1 FxLMS算法框图
其中:x(n)是传声器在噪声源处采集的参考信号,P(z)表示x(n)传递到人耳的初级通路,d(n)作为期望信号,W(n)是线性横向滤波器,可输出次级噪声信号u(n)。S(z)表示u(n)传递到人耳的次级通路是S(z)的估计,理论上两者是相等的。xf(n)是滤波输入信号,y(n)表示次级声波,与d(n)相抵消并产生误差信号e(n)。
FxLMS算法以最小均方误差为准则,基于最速下降法的原理进行计算,其计算过程如下:
1)计算滤波器的输出信号u(n)

式中:w(n)=[w(1),w(2),…,w(L)]是滤波器的系数向量,x(n)=[x(L),x(L-1),…,x(1)]是对应的输入信号向量,T 表示转置运算,L 表示滤波器的长度。
2)输出信号u(n)传递到人耳

式中:*表示线性卷积运算,s(n)是S(z)的脉冲响应。
3)误差信号e(n)可表示为

4)计算滤波x信号xf(n)
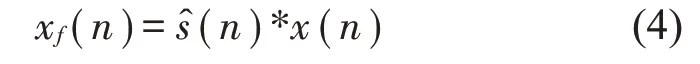
5)最后自适应更新滤波器W(n)的系数
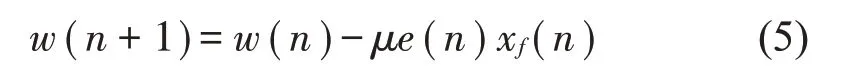
式中:μ为步长因子,它的收敛范围如下式所示

式中:L 是滤波器的长度,pfx是滤波输入信号的功率,Δ 是因次级通道的存在而导致的延迟。
2 MFxLMS算法
在FxLMS算法中,因为次级通道的存在而导致的延迟会降低算法的收敛速度。在MFxLMS 算法中,增加了一个辅助路径以解决该问题,如图2所示。

图2 MFxLMS算法框图
图2中,辅助路径用于修正误差信号,即为


滤波器系数自适应更新时从而避免了采用FxLMS算法,而是直接应用LMS算法

此时,步长因子μ的收敛范围变为

由于2/LPfx>2/(L+Δ)Pfx,可以选取较大的μ,因此MFx LMS 算法的收敛性能会得到一定程度的提高。
3 变步长方法
3.1 变步长函数
为解决传统FxLMS 算法不能同时兼顾收敛速度和稳态误差的缺陷,文献[12]优化了μ值的调整原则,提出一种基于反正切函数的VS-FxLMS算法,在算法处于初始阶段或人耳周围声环境变化较大时,使μ取得一个较大值以提高算法的收敛速度和更好跟踪环境的变化;随着算法趋于收敛,误差信号将逐渐变小,使μ 值也跟着变小,以提高算法的估计精度,同时μ值的减小也会使误差信号进一步降低,直到算法达到一个最优的收敛状态。
文献[12]提出的变步长函数如下
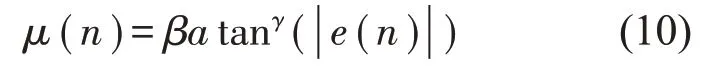
式中:a tan表示反正切函数,α、β、γ为参数。
从式(6)中可以看出,如果输入信号功率变化较大或有脉冲信号时,为保证输入信号功率最大时的收敛稳定性,必须牺牲输入信号功率较低时的收敛速度,通过对输入信号功率归一化处理可以有效改善这一不足。
本文基于修正反正切函数和归一化的方法,提出一种新的变步长函数,即

将其应用到MFxLMS算法上,此时式(9)对滤波器进行自适应更新的迭代公式变为
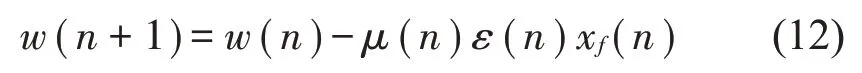
3.2 参数分析
由于式(11)有3个参数,这里将定性分析不同参数值对算法收敛性能的影响。分析过程中,由于式(11)分母部分是为了化解输入信号功率对算法收敛速度的影响,可以先不给予考虑。主要根据μ(n)函数分子部分采用控制变量法进行分析。通过调整不同参数值,得出μ(n)值与e(n)值的一系列函数曲线,如图3 所示,其中μ(n)值大小一定程度上反映了算法的收敛速度,而曲线一定范围的波谷宽度反映了算法的稳定性。
由图3(a)可以看出,α 值对μ(n)值大小和波谷宽度影响都比较大。α值越大,μ(n)值越大,曲线的开口越窄,此时算法的收敛速度整体较快,但波谷的宽度较窄,表示算法在达到收敛时,能够维持稳态误差较高精度的能力降低;如果α值越小,则刚好与其相反,但波谷宽度不宜过大,否则变步长函数将退变成固定步长因子的状况。
由图3(b)可以看出,β值整体上对曲线的波谷宽度影响较小,主要对μ(n)值大小带来影响。由于β是函数方程的外围系数,可用于限制μ(n)值的界限,β 值的选取应确保μ(n)值处于算法的收敛范围之内。
由图3(c)可以看出,γ 值对μ(n)值大小和波谷宽度也都有影响。γ值越大,μ(n)值越大,波谷宽度越宽。而γ 的取值不宜过大,否则会造成变步长函数的计算量成指数级的增长,反而会影响算法的稳定性。
通过以上的分析可知不同参数值对算法的收敛性能影响不同,且同一个参数的不同取值对算法的收敛性能影响也很大。由于在分析过程中,并未考虑到式(11)分母中输入信号功率对算法收敛性能的影响。因此在实际应用中,可以参考以上的分析对参数进行调试,最终可以得出算法较好的收敛状态。

图3 μ(n)与e(n)的函数曲线
4 汽车车内噪声采集
采集汽车车内噪声信号的试验选用车辆为荣威某款轿车,该车为4 门5 座3 厢车,外形长、宽、高为4 624 mm×1 827 mm×1 480 mm,在市面上较为常见,具有较强的代表性。实验场所为上海工程技术大学半消声室,采集设备为西门子生产的噪声与振动数据采集设备LMS.test.Lab,如图4所示。

图4 汽车车内噪声采集
数据采集依据国家标准GB/T 18697_2002 (声学—汽车车内噪声测量方法)进行。汽车车内噪声的采集分两组,一组是汽车处于怠速工况,噪声为稳态噪声;另一组是汽车发动机转速从0增加到3 000 r/min 并保持一段时间的工况,期间还有突发噪声,在红色线圈内可见,噪声为非稳态噪声。每组采集时间均为10 s,并通过归一化幅值显示,如图5所示。

图5 车内噪声采集信号
5 仿真实验
通过计算机在MATLAB 环境中对所采集车内噪声进行有源控制仿真实验。所用车辆车内噪声初级通路传递函数以及次级通路传递函数分别为[0.001 0.005-0.5 0.75 0.9 0.75 0.5 0.2-0.35-0.01]和[0.01-0.01 0.95 0.01-0.75]。
考虑到次级通路的影响,在进行仿真之前,首先对车内次级通路进行拟合。为保证次级通路拟合精度,的初始长度要比S(z)长一些,设置的长度为8,其拟合结果如图6 所示。可以看出,的前5 个数据与S(z)完全重合,后3 个数据是0,说明已经达到了较为理想的拟合状态。

图6 次级通路的拟合
将所提出变步长方法应用到MFxLMS 算法和FxLMS 算法上,可分别实现VS-MFxLMS 算法和一种新的VS-FxLMS算法。分别应用VS-MFxLMS算法、VS-FxLMS 算法以及MFxLMS 算法对所采集车内噪声进行有源控制。通过对MFxLMS 算法的步长因子进行调试,得出当MFxLMS算法处于最佳收敛状态时μ=0.08;再对式(11)中的各个参数进行调试,得出VS-MFxLMS 算法和VS-FxLMS 算法的各参数值如表1所示。

表1 参数值
(1)实验一为车内稳态噪声有源控制
首先应用各种算法对所采集车内稳态噪声进行有源控制,结果如图7所示,并分别计算各种算法对车内稳态噪声进行有源控制后误差信号幅值均值,其结果如表2所示。
从表2中可以看出,VS-MFxLMS算法的稳态误差与MFxLMS 算法相比,降低了55 %;与VSFxLMS算法相比,降低了28%。

图7 车内稳态噪声有源控制结果

表2 车内稳态噪声有源控制误差均值
图8 给出了3 种算法对车内稳态噪声进行有源控制的收敛速度对比,其中横轴表示迭代次数,纵轴表示均方误差(Mean Square Error,MSE)。
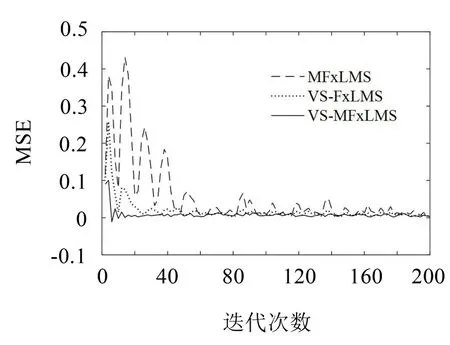
图8 车内稳态噪声有源控制收敛速度对比
从图9 中可以看出,MFxLMS 算法在迭代60 次左右时收敛,VS-FxLMS 算法在迭代24 次左右时收敛,而VS-MFxLMS算法在迭代15次左右就已收敛。与MFxLMS 算法相比,VS-MFxLMS 算法的收敛速度提高了3 倍左右,与VS-FxLMS 算法相比,VSMFxLMS算法的收敛速度提高了60%左右。
(2)实验二为车内非稳态噪声有源控制
应用各种算法对所采集非稳态车内噪声进行有源控制,结果如图9 所示。分别计算各种算法对车内非稳态噪声进行有源控制后误差信号幅值均值,其结果如表3所示。
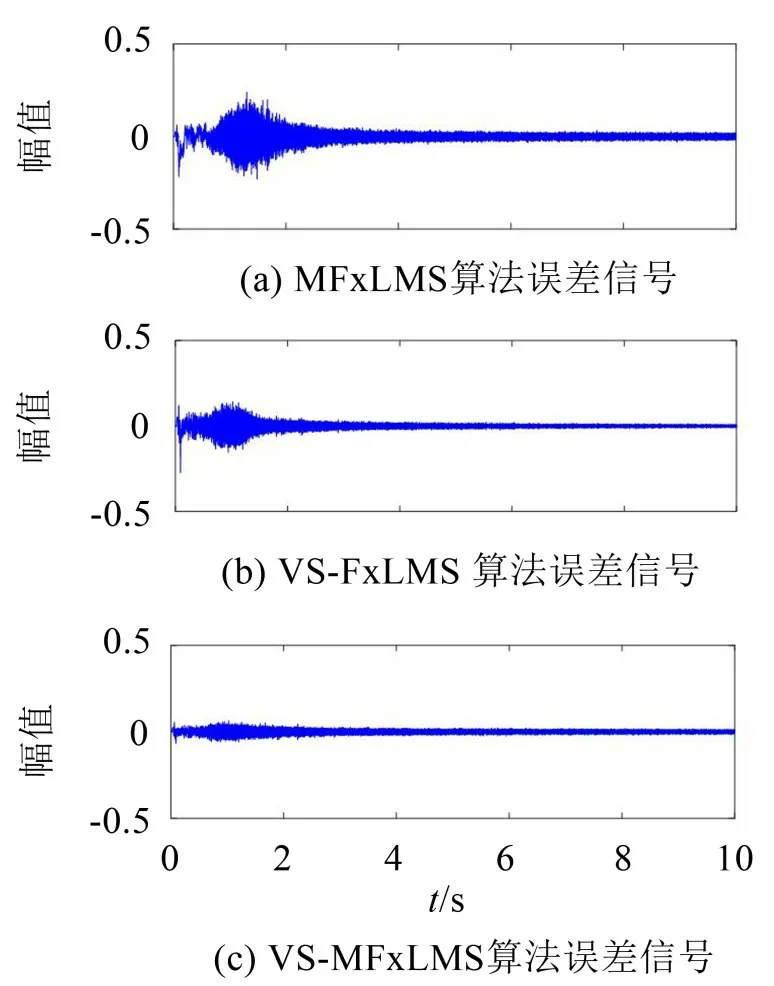
图9 车内非稳态噪声有源控制结果

表3 车内非稳态噪声有源控制误差均值
从表2中可以看出,VS-MFxLMS算法的稳态误差与MFxLMS 算法相比,降低了60 %左右;与VSFxLMS算法相比,降低了32%左右。
图10给出了3种算法对车内非稳态噪声进行有源控制的收敛速度对比。

图10 车内非稳态噪声有源控制收敛速度对比
从图10 中可以看出,MFxLMS 算法在迭代100次左右时收敛,VS-FxLMS 算法在迭代50 次左右时收敛,而VS-MFxLMS 算法在迭代40 次左右就已收敛。与MFxLMS 算法相比,VS-MFxLMS 算法的收敛速度提高了1.5 倍左右,与VS-FxLMS 算法相比,VS-MFxLMS算法的收敛速度提高了25%左右。
综合以上2种情况,说明VS-MFxLMS算法对车内噪声的有源控制具有更好的效果。
6 结语
由于LMS 算法未考虑到汽车车内噪声有源控制系统中次级通路对算法稳定性的影响,相比之下,FxLMS算法以及MFxLMS算法具有更好的实用性。应用MFxLMS 算法、VS-FxLMS 算法和VSMFxLMS算法分别进行汽车车内噪声有源控制。结果表明,VS-MFxLMS 算法解决了MFxLMS 算法的缺陷,且与VS-FxLMS 算法相比具有更快的算法收敛速度和较小的稳态误差。

