汽车钢板弹簧动力学建模及应用研究

杨 超，刘夫云，赵亮亮，王秋花，张秋峰

（桂林电子科技大学 机电工程学院，广西 桂林541004）

钢板弹簧作为商用车悬架的主要部件，具有结构简单、制造维修方便、传递力性能好等特点[1]。目前，对板簧动力学建模研究非常广泛，席敏等提出将有限元法和多体动力学法相结合，考虑片间接触建立板簧动力学模型，并将该模型应用于载货汽车的平顺性分析，验证了该建模方法具有较高建模精度[2]；李小龙等结合离散及柔性体理论，利用ADAMS 板簧工具箱建立板簧动力学模型，并通过仿真结果与理论设计值对比，验证模型的正确性[3]；魏慧利等对目前板簧的几种建模方法以及建模途径进行了对比分析，并且总结出各种建模方法的建模步骤和理论、优缺点以及适用范围[4]；孙学民等采用ANSYS建立了汽车钢板弹簧的有限元模型，并分析钢板弹簧模型在不同摩擦因数条件下对应力和位移响应的影响[5]；秦东晨等提出利用中性面方法建立的板簧模型，减少整车仿真模型的自由度，有效提高ADAMS仿真计算速度和精度[6]；沈香等通过对前悬架以纵置对称式板簧为弹性元件兼导向杆件的非独立悬架在板簧变形过程中运动轨迹进行分析，探讨板簧变形对客车前轮定位参数的影响[7]；余龙等利用ADAMS 建立了板簧动力学模型，将该模型应用于整车虚拟样机模型，并通过平顺性仿真，分析板簧模型在不同的刚度下对汽车行驶平顺性的影响[8]；姚春革等采用HyperMesh 和ANSYS 联合仿真的方法建立多片板簧三维有限元模型，分析不同接触摩擦系数条件下多片板簧的总成位移、Mises 应力、静刚度特性，并通过与试验结果对比，得出摩擦系数为0.2时最接近实际情况[9]；芦荡等研究了钢板弹簧模型中动态参数与变形历程的关系，并建立可用于汽车动态仿真的钢板弹簧动态力模型并辨识了模型参数[10]；H Gong 等采用离散梁法，在多体动力学软件ADAMS 中建立板簧动力学模型，通过仿真计算其刚度，并与实测数据进行对比[11]；在国外学者的研究中，U Prasade 等开发了梁单元的钢板弹簧模型，并对钢板弹簧的动静态特性进行了研究[12]；Bartosz Kadziela等提出了一种可用于整车模拟的板簧模型建模方法，能够有效模拟板簧的刚度特性，并运用于整车仿真分析；在上述学者的研究中，主要研究了钢板弹簧动力学模型的刚度、强度等特性，但并未考虑钢板弹簧的实际运动特性对整车行驶平顺性的影响。

对此，本文对钢板弹簧的动态特性对其刚度特性和整车平顺性的影响进行研究。根据运动学理论，推导出钢板弹簧运动学特性的计算公式，并分析钢板弹簧的运动特性对其弹性恢复力和阻尼力的影响；利用Hyper Mesh 和ANSYS 建立板簧的三维有限元模型，进行模态计算，得到板簧各片的模态中性文件，导入ADAMS进行装配得到板簧动力学模型，并对装配好的板簧动力学模型进行静平衡仿真计算及试验，验证模型的准确性；同时将该模型应用于整车动力学模型，通过整车平顺性仿真，分析板簧的运动特性对整车平顺性的影响。

1 钢板弹簧的运动特性分析

在整车平顺性仿真分析时，传统的钢板弹簧动力学模型并未考虑其运动特性对整车乘坐舒适性的影响；对此，本文根据运动学理论[11]，推导钢板弹簧的运动学特性计算公式，并分析钢板弹簧的运动特性对其弹性恢复力和阻尼力的影响。

1.1 不考虑吊耳的钢板弹簧模型运动特性分析

当不考虑吊耳的作用时，后端卷耳与车架采用平面滑动连接；因此，设钢板弹簧的卷耳半径为r，前端参与变形长度为L，曲率半径为R，张角为α，不参与变形长度为s（U型螺栓加紧段），板簧的中心安装点坐标为N(x,z)，如图1所示。

图1 不考虑吊耳的板簧分析模型

根据运动学理论分析，以前端卷耳中心为坐标系原点，则有

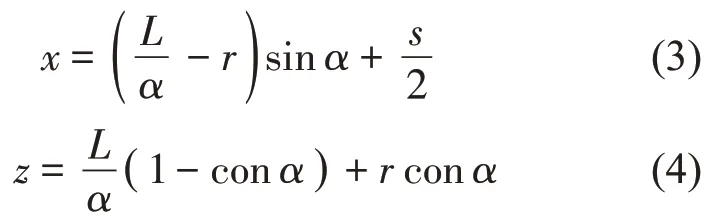
由于α比较小，取正弦和余弦3阶以下的近似值

将式（5）、式（6）代入式（3）、式（4）得到

解得板簧中心安装点N(x,z)以z为参变量的运动方程

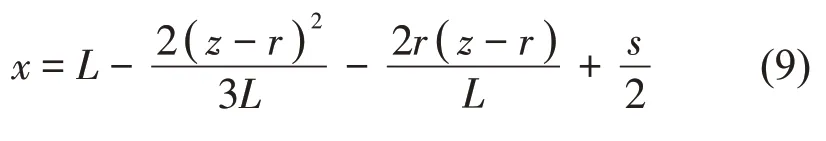
1.2 考虑吊耳的钢板弹簧模型运动特性分析

当考虑吊耳的作用时，吊耳与后端卷耳采用摆动铰链连接；因此，设摆动吊耳中心距为f，吊耳固定端的中心点坐标为A(x1,z1)，后端卷耳的中心坐标为B(x0,z0)，卷耳中心距为M，如图2所示。

根据运动学理论分析，以前端卷耳中心为坐标系原点，则卷耳中心距M为

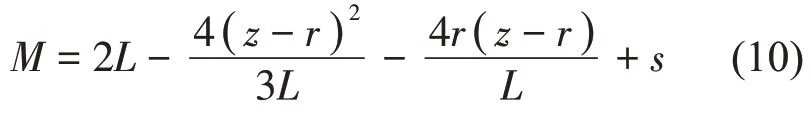
当板簧的中心安装点受到载荷P 作用时，后端卷耳的中心点B(x0,z0)以吊耳固定端的中心点A(x1,z1)为圆心，以f为半径作圆周运动；同时，又以前端卷耳的中心为圆心，卷耳中心距M 为半径作圆周运动。

图2 考虑吊耳的板簧分析模型

由此得到后端卷耳的中心点B(x0,z0)的运动方程如下

将式（11）进行合并，得到

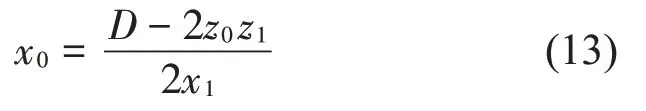
采用消元法，代入式（9），得到

简化后，得到

解得后端卷耳中心点B(x0,z0)以z0为参变量的运动方程

1.3 静态平衡计算分析

假设板簧的静刚度为K，板簧的中心安装点N(x,z)受到垂直载荷P的作用。

当不考虑吊耳作用时，后端卷耳只能发生水平位移，此时板簧中心点N(x,z)的变形量为：

垂向变形量为

水平变形量为Δx

将Δz 代入式（9），可解得板簧的中心点的水平位移Δx。

当考虑吊耳的作用时，后端卷耳分别以前端卷耳和吊耳固定端为圆心做圆周运动，此时中心点N(x,z)的变形量为

垂向变形量

水平变形量

其中：Δz0为后端卷耳中心的垂向位移，Δx0为后端卷耳中心的水平位移；将Δz 代入式（15）可求得Δz0、Δx0。

由于钢板弹簧的弹性恢复力的变化形态取决于垂向位移的变化，而阻尼力的变化取决于垂向速度的变化；从上述公式推导计算得知，垂向变形量Δz′>Δz，水平变形量Δx′>Δx，产生的加速度a′=因此，可以推断出在同等条件下，板簧中心安装点受到垂直载荷P 作用时，考虑吊耳的板簧的运动特性与实际模型更加接近，可以更好地分析板簧的运动特性对其弹性恢复力和阻尼力的影响。

2 钢板弹簧动力学建模方法

2.1 钢板弹簧动力学模型建立

在整车平顺性仿真分析中，传统的钢板弹簧动力学模型存在仿真精度低、未考虑运动特性等问题。基于本文中板簧的运动特性分析，建立板簧动力学模型，其相关的结构尺寸参数如表1 所示。板簧的材料采用60CrMnBa，其具体的参数如表2所示。

钢板弹簧动力学建模可以概括为以下步骤：

（1）根据企业提供的板簧外形结构尺寸，通过三维软件Solid Works 建立板簧的三维几何模型，并进行装配；

（2）将Solid Works装配好的板簧三维几何模型导入Hyper Mesh 中进行网格划分，其网格均采用8节点六面体单元，通过分割、映射和合并节点来划分，单元尺寸大小为8 mm，并且创建属性文件以及赋值；

（3）将划好网格的板簧有限元模型导入ANSYS中进行模态计算分析，得到每片板簧的模态中性文件。

表2 钢板弹簧材料参数

（4）将板簧各片的模态中性文件依次导入多体动力学软件ADAMS 中进行装配，得到钢板弹簧动力学模型，如图3所示。

图3 钢板弹簧动力学模型

将模态中性文件导入ADAMS 进行装配后，得到的板簧动力学模型并没有受到任何约束；因此，需要根据板簧与车架以及车桥的实际连接方式，对板簧动力学模型添加约束和施加载荷。通过板簧的接触理论与试验的方法，确定板簧片与片之间的接触刚度K =10 000 kN/mm、动摩擦系数μ=0.18 以及静摩擦系数μ0=0.25。

对定义好边界条件的板簧动力学模型进行静态特性仿真分析，将集中载荷均匀施加在末片板簧的U 型螺栓夹紧区域上，施加载荷P 为3 kN 至15 kN，施加载荷间隔为1 kN；将得到的仿真结果与测试结果进行对比分析，验证了板簧动力学模型的刚度特性。

2.2 静态特性验证

根据国家标准GB/T19844-2005《钢板弹簧》，对板簧进行动静态测试；本文采用用于钢板弹簧台架试验的PWS-20 动静态试验机，对11 片板簧进行刚度测试，如图4所示。

图4 钢板弹簧台架试验

在实际测试中，通过压盘对板簧中部施加载荷，测量板簧在不同的外部载荷作用下的变形；板簧的实测与仿真的位移-载荷曲线如图5所示。

从折线图中可以得出，板簧在不同外载荷的作用下，载荷与位移基本是线性变化的；通过对数据的计算分析，得出板簧静刚度的试验测试值为446.06 N/mm、有吊耳的板簧仿真值为474.77 N/mm、无吊耳的板簧模型的仿真值为519.39 N/mm，其相对误差分别为k1=6.44%，k2=16.4%。结果表明：板簧静态刚度的仿真结果与试验结果基本吻合，能够较好反映板簧刚度特性。

图5 钢板弹簧位移-载荷曲线

表1 钢板弹簧的结构尺寸参数/mm

3 钢板弹簧动力学模型应用

以前在建立整车动力学模型时，将板簧简化为具有一定静刚度特性和阻尼的减震器模型，并未考虑板簧的动态特性以及运动特性对平顺性的影响；因此，为了分析板簧动力学模型对整车平顺性的影响，将建立好的板簧动力学模型应用于整车动力学模型，如图6所示。

图6 整车动力学模型

3.1 基于MATLAB建立随机路面

本文利用MATLAB/Simulink 建立路面随机激励生成模型，如图7所示。

在整车动力学模型仿真分析时，后轮的路面随机激励输入与前轮的路面随机激励存在一定的滞后。

图7 MATLAB/Simulink路面随机激励生成模型

因此，根据路面随机激励生成模型，设置车速v=30 km/h～90 km/h，前后轮距B=2 045/1 860（mm），轴距3 800/5 250（mm），采样时间T=120 s 以及B 级路面不平度系数G=64×10-6m3，生成在B级路面上车辆以30 km/h～90 km/h的车速行驶的路面随机高程位移并应用于整车平顺性仿真。

3.2 平顺性仿真分析

在平顺性仿真分析中，设整车动力学模型分别以30 km/h、40 km/h、50 km/h、60 km/h、70 km/h、80 km/h 以及90 km/h 的车速在B 级路面上行驶，并以座椅为仿真测试点，测试在不同的速度工况下座椅的垂向加速度均方值。在实际车型平顺性测试中，采用Prosing系列的P8004汽车平顺性测试系统对行驶在高速公路上的实车进行数据采集，再通过DATS分析系统对数据进行分析处理，其中采用的传感器类型为3轴坐垫加速度传感器356 B41。

对数据作进一步处理，得到结果的曲线图和数据表分别如图8和表3所示。

从图8 中可知，得到的仿真结果与测试结果的趋势基本一致，能较好地反映整车性能。通过对数据作进一步分析发现，考虑钢板弹簧模型的整车平顺性仿真结果与试验测试结果更加接近。

由于在建立整车动力学模型时，简化了整车模型，并且在MATLAB中建立的随机仿真路面与实际也具有一定的差异；因此，平顺性仿真结果与测试结果存在一定的误差。

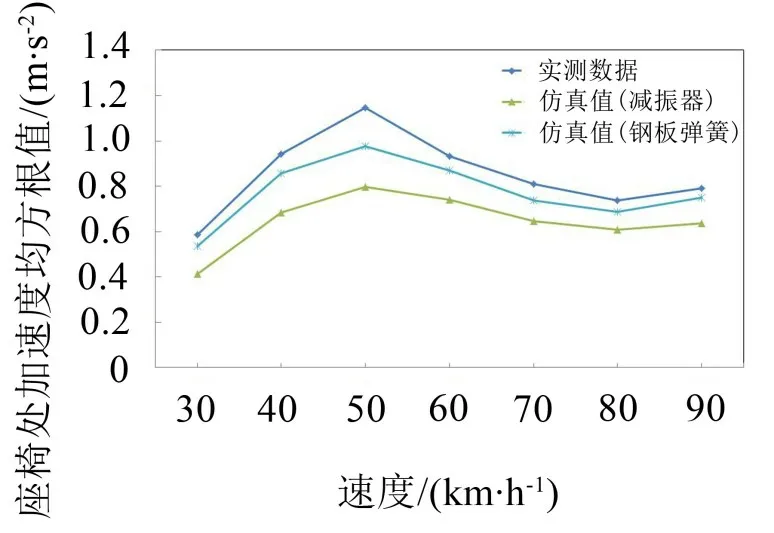
图8 座椅垂向加速度的仿真与实测数据曲线

4 结语

本文主要研究钢板弹簧的动态特性对其刚度特性和整车平顺性的影响。

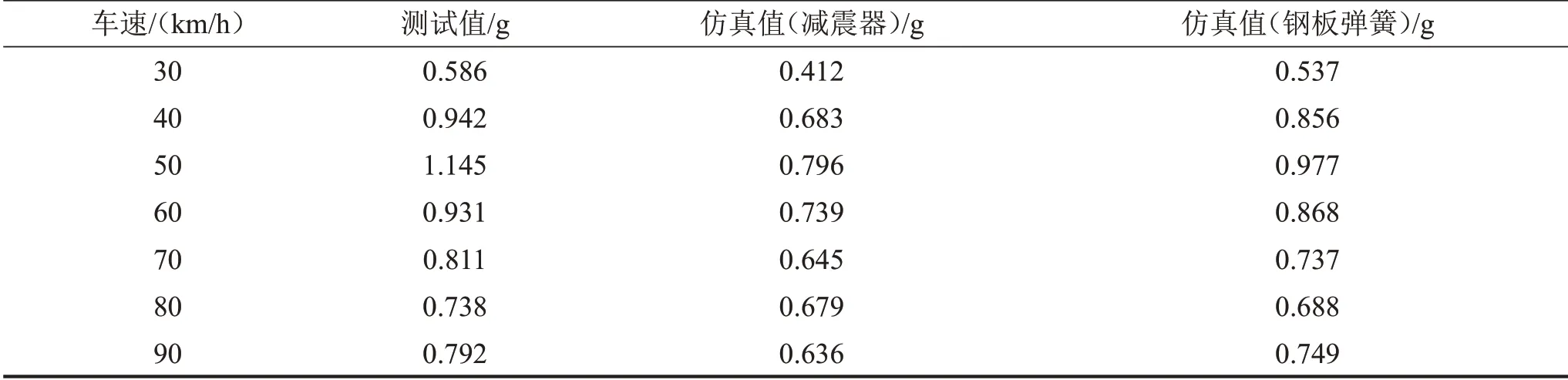
表3 座椅垂向加速度均方值

（1）根据运动学理论，推导钢板弹簧的运动特性计算公式，并分析钢板弹簧模型的运动特性对其弹性恢复力和阻尼力的影响。

（2）基于板簧的运动学特性分析，建立板簧动力学模型。将该模型应用于在ADAMS中建立的整车动力学模型，并假设车辆以30 km/h、40 km/h、50 km/h、60 km/h、70 km/h、80 km/h 以及90 km/h 的车速在B 级随机路面上行驶，进行整车平顺性仿真分析。通过数据分析发现，本文建立的钢板弹簧模型与单纯将钢板弹簧简化为具有静刚度和阻尼的减震器模型相比，其平顺性仿真结果与实际更为接近。