基于精细复合多尺度熵和自编码的滚动轴承故障诊断方法

郑近德，潘海洋，包家汉，刘庆运，丁克勤，欧淑彬

（1.液压振动与控制教育部工程研究中心，安徽 马鞍山243032；2.安徽工业大学 机械工程学院，安徽 马鞍山243032；3.中国特种设备检测研究院，北京100029）

轴承是工业领域最重要也是最脆弱、最容易发生故障的零部件。目前轴承健康监测与故障诊断的研究已经引起相当大的关注。能否准确有效地提取状态特征信息是轴承监测和诊断的关键。由于轴承存在刚度、摩擦和载荷条件的瞬态变化，机械系统常常表现出非线性、非平稳行为，致使其振动信号复杂，表现出有非线性和非平稳特征[1]。常用的时域分析、频域分析和时频分析方法等在处理这类信号时难免存在一定的局限性。而非线性分析方法由于能够准确有效地提取这类振动信号的非线性、非平稳的状态特征信息而得到了广泛关注。

在非线性动力学分析方法中，基于熵理论建立的时间序列复杂度测量方法，如信息熵[2]、近似熵[3]和样本熵[4]，都已被成功应用于机械故障诊断中[5–7]。然而，单一尺度的熵算法并不能有效测量时间序列的复杂性[8–9]。为了克服单一尺度的不足，Costa等提出了衡量不同粗粒化时间序列复杂性的多尺度熵算法(Multiscale Entropy，MSE)[8,10–11]。郑 近 德 等[12]将MSE 应用于机械故障诊断中，结果表明，MSE 能够有效地实现故障的识别。陈慧等[13]将MSE 与PNN结合成功应用于滚动轴承故障诊断中。然而，在MSE 算法中，随着尺度因子的增加，粗粒时间序列会迅速变短而导致不精确的熵估计或引起未定义熵，而且熵值的误差也将随着粗粒化时间序列长度的迅速变短而增大。为了克服MSE方法的不足，文献[14]提出了一种新的改进多尺度熵算法—精细复合多尺度熵(Refined composite multiscale entropy，RCMSE)，RCMSE 能够弥补MSE 的缺陷，且得到的熵值的一致性和稳定性更好。

由于提取的多尺度熵值特征维数较高，存在一定的信息冗余，藴藏故障状态的特征信息不能被有效利用，影响故障识别效果。流形学习算法是基于拓扑流形概念而提出的降维方法，能够实现维数约减和数据可视化，考虑将其应用于高维特征数据的可视化降维。由于现实中大多数高维数据具有非线性结构，线性降维方法不可避免地存在一定的局限性，而非线性流形学习自编码降维方法能够有效实现非线性高维数据的降维[15–17]，文中考虑将其应用于滚动轴承故障特征的降维与可视化。为了实现故障智能诊断，需要选择合适的分类器，支持向量机作为一种成熟的分类器，受惩罚因子和核参数影响较大，遗传优化算法[18]能够对SVM 的参数进行优化，自动搜索最佳参数组合，避免了依赖人为的设定和不必要的干扰[19]。在此基础上，结合精细复合多尺度熵、自编码降维技术和遗传算法优化支持向量机多模式分类器，提出了一种新的滚动轴承故障智能诊断方法。最后，将提出的方法应用于试验数据分析，结果表明，提出的方法不仅能够有效地诊断出轴承不同故障，而且识别率较高。

1 精细复合多尺度熵

1.1 多尺度熵和复合多尺度熵

对于时间序列X={xi,1≤i ≤N}，第τ 个尺度粗粒化时间序列定义如下

在传统MSE算法中，不同尺度因子τ下的MSE被定义为尺度因子τ下第一个粗粒化时间序列的样本熵，即MSE(x,τ,m,r)=SampEn(y(τ)1,m,r)。但是，对于短时间序列的分析，MSE在较大时间尺度下往往会引起未定义样本熵值。为此，引入了CMSE 来提高MSE算法的精度。

CMSE算法中，在尺度因子τ下计算所有粗粒化时间序列的样本熵，CMSE值是由τ个样本熵取平均而得到，即

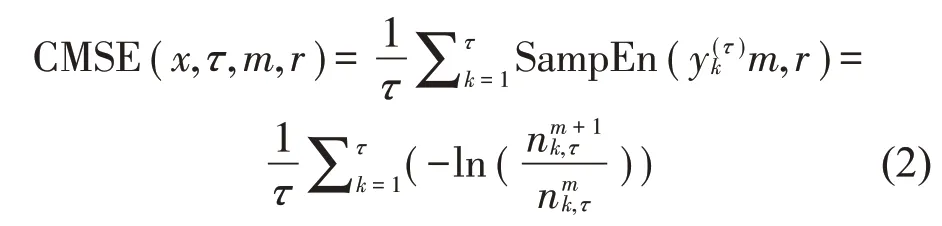
1.2 精细复合多尺度熵

RCMSE 算法解决了上述MSE 和CMSE 方法的不足，主要步骤如下：

(1)利用式（1）粗粒化程序获得不同时间尺度的粗粒化时间序列；

(2)在尺度因子τ 下，计算全部τ 个粗粒化序列匹配向量对和的数目；

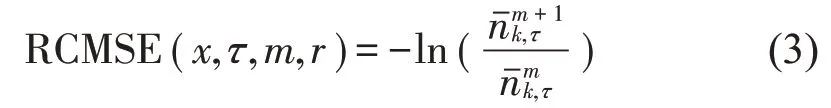
对上式进行简化，得

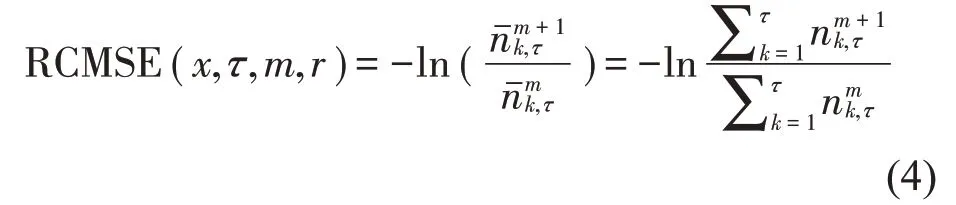
根据式（4）可知，仅仅当全部nmk,τ和nm+1k,τ都为零时，RCMSE 才会有未定义熵值。因此，相较于CMSE算法，RCMSE算法大大降低了未定义熵的可能性，得到的熵值一致性和稳定性更好。

2 基 于RCMSE 和Autoencoder 的 滚动轴承故障诊断方法

2.1 方法步骤

RCMSE 弥补了MSE 和C MSE 提取信号特征时熵估计不精确的缺点，得到的熵值具有更强的稳定性。文中考虑采用RCMSE 方法来提取各状态振动信号的复杂性故障特征信息。同时，由于特征维数较多，高维数据掩盖了有效特征信息，考虑采用Autoencoder 流形学习降维算法对高维特征向量矩阵进行降维，挖掘具有内在规律的低维流形特征。最后，为了实现智能诊断，采用训练速度快、适合小样本分类的支持向量机进行模式识别。同时针对支持向量机的分类结果通常会受到惩罚因子c和核函数参数g 的影响等问题，采用自适应概率遗传优化算法(Genetic algorithm，GA)对SVM 中的参数c 和g进行优化，建立基于GA-SVM 的多类模式分类器，以对降维后的低维流形故障特征向量进行识别。

综上，基于RCMSE、Autoencoder 降维算法和GA-SVM的滚动轴承故障诊断方法的步骤如下：

(1)假设滚动轴承故障和正常等状态共有K类，每种状态有Nk组振动信号(k=1，2，…K)；

(2)计算每类Nk组振动信号样本的RCMSE，每组样本得到τmax个特征值，组成高维特征向量集RN×τmax，其中是最大尺度因子，一般取20；

(3)采用Autoencoder降维算法对高维特征向量矩阵进行降维，得到低维流形特征RN×I，I 是降维后的维数；

(4)每种状态随机取1/2Nk组组成训练样本，其余作为测试样本，将训练样本输入到基于GA-SVM多类模式分类器进行训练；

(5)将测试样本输入到训练好的GA-SVM 分类器，根据GA-SVM分类器输出确定滚动轴承的工作状态和故障类型。

2.2 实验验证

为了验证所提方法的有效性，将其应用于美国Case Western Reserve University 的滚动轴承试验数据[20]。测试轴承为6205-2RS JEM深沟球轴承，使用电火花加工技术在轴承上布置单点故障。考虑转速为1 730 r/min、负载3 HP条件下，正常轴承以及直径大小为0.177 8 mm、深度为0.279 4 mm的外圈、内圈故障和滚动体故障的滚动轴承振动信号，采样频率为12 kHz，采集到具有局部单点内圈（Inner Race Fault，IRF）、外圈（Outer Race Fault，ORF）、滚动体故障（Ball Element Fault，BEF）和正常（Normal，NOR）4种状态的振动信号，每种状态取29组数据，每组数据长度为4 096个采样点，4种状态下轴承的振动信号时域波形如图1所示。

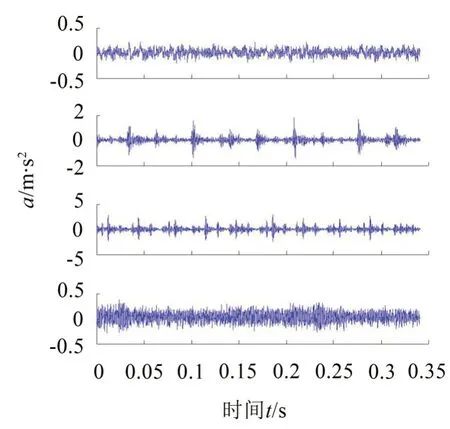
图1 4种状态下轴承振动信号的时域波形

由于背景噪声及干扰，从时域波形上很难区别这4 种状态。将提出的方法应用于实验数据分析，具体步骤与分析如下：

首先，计算滚动轴承每种状态振动信号的RCMSE，每种状态取29组样本，每组样本得到20个特征值，4 种状态共得到116 组样本，组成原始特征向量矩阵R112×20。

4 类状态下的RCMSE 均值标准差曲线如图2所示。

图2 4类状态下滚动轴承的RCMSE均值标准差图

从图2中可以看出，在大部分尺度上，正常轴承的振动信号熵值较大，且随着尺度因子的增大变化平缓；而3 种具有故障的滚动轴承的振动信号的RCMSE曲线出现明显的逐渐递减趋势。其次，采用Autoencoder 流形学习算法对高维特征空间进行特征降维，得到低维特征向量集，压缩后的低维特征二维和三维流形如图3(a)和图3(b)所示。

从图3 可以看出，降维后的二维和三维流形特征都能很明显地将各状态特征集分开。再次，对每种状态各取15组样本构成训练样本特征集R60×3，将训练样本集输入到基于GA-SVM 多类模式分类器中进行训练（一对一构建SVM 多模式分类器）。采用遗传算法优化SVM 中惩罚参数c 和核函数参数g，将对训练样本特征集进行交叉验证(Cross Validation，CV)意义下的识别率作为GA中的适应度函数值，设定CV参数为5，GA算法中的最大迭代次数为200，种群数量为20，代沟为0.9，交叉概率为0.7，变异概率为0.2。搜索到的最佳惩罚因子c 为0.233 46，核函数参数g 为15.730 1。用训练好的GA-SVM多模式分类器对测试样本特征集进行分类预测。根据GA-SVM 分类器的输出值确定滚动轴承的工作状态和故障类型：1-正常，2-外圈故障，3-内圈故障，4-滚动体故障。预测的输出结果如图4所示。

图3 Autoencoder降维后二维流形和三维流形

图4 基于本文方法的GA-SVM分类结果

从图4 可以看出，GA-SVM 预测的所有测试样本都得到了正确分类，识别率为100%。

为了说明RCMSE 方法在特征提取方面的优势，再提取4类原始信号的MSE，如图5所示。并将RCMSE和MSE的标准差进行对比分析，结果如图6所示。从图6中可以看出，在尺度因子较小时，特别地τ<11时，4种状态的熵值很难区分，有交叉重叠现象，而只在较大尺度时4 类样本的熵值才能明显区分。对比图5 的RCMSE 曲线可知，RCMSE 方法得到的4种状态的熵值曲线在所有尺度上两两都能够明显区分开来，并没有交叉重叠现象。不仅如此，从图6 中各状态的RCMSE 与MSE 标准差对比可以看出，各状态下提取的RCMSE 标准差波动性较小，而MSE 标准差波动性较大，而且在大部分尺度上，正常和故障滚动轴承的RCMSE的标准差都小于MSE的标准差。

图5 4类状态的轴承振动信号的多尺度熵

为了验证Autoencoder算法在降维方面的优势，将其与常用的降维算法LDA(Linear Discriminant Analysis，LDA)[21]对 比，分 别 采 用Autoencoder 和LDA对各类状态的MSE特征进行降维，降维后的二维和三维流形如图7(a)、图7(b)和图8(a)、图8(b)所示。

从图7 中可以看出，根据Autoencoder 算法得到的二维和三维流形分布都能够将4种状态轴承明显分开；而图8 中根据LDA 降维后的3 类故障的二维和三维特征分布混淆在一起，难以分类识别。对比结果验证了Autoencoder降维的优越性。

最后，为了说明SVM 参数优化的必要性，将采用LDA降维后的低维特征输入到SVM中进行训练与测试，c 为2，g 为1，预测分类结果如图9(a)所示。从图中可以看出，有18 个测试样本被错分，识别率为67.8571 %。而采用GA-SVM 进行分类预测，结果如图9(b)所示，优化参数为c=1.661 5，g=6.582 3。得到的故障识别率为76.785 7%，相较于SVM 提高了8.928 6%。这进一步说明了采用遗传算法优化SVM的必要性和优越性。

3 结语

(1)介绍了一种新的衡量振动信号复杂性的算法——精细复合多尺度熵（RCMSE），其能够克服多尺度熵在提取信号特征时产生不精确的熵估计的不足，仿真与试验分析结果表明，与MSE 相比，RCMSE能够更精确地提取振动信号故障特征信息，得到的熵值一致性和稳定性更好。

图6 不同状态轴承RCMSE与MSE标准差对比

图7 Autoencoder降维后二维和三维特征分布

图8 LDA降维后二维和三维特征分布

图9 基于LDA降维特征的SVM和GA-SVM分类结果

(2)将Autoencoder降维技术应用于高维故障特征降维，得到具有拓扑流形结构的低维可视化特征，试验分析结果表明，相较于LDA，Autoencoder 在降维方面更具有优势。

(3)提出了一种新的基于RCMSE、Autoencoder降维和GA-SVM的滚动轴承故障诊断方法，仿真和试验分析结果表明，与现有方法相比，所提方法在故障特征提取、高维数据可视化降维和模式识别精度方面具有明显的优势。