基于驾驶质量的城市轨道交通乘务排班优化研究

刘 杰， 代佳妮

(重庆公共运输职业学院 运输贸易系，重庆402247)

0 引 言

城市轨道交通运营公司通过采取加开临客、提高行车密度等方式来满足与日俱增的客运需求，却导致城市轨道交通排班复杂，直接影响驾驶员的驾驶状态和驾驶效能，而城市轨道交通驾驶员对于驾驶质量担负有重要的责任，因此，如何合理制定乘务排班计划，科学安排驾驶员作息时间就显得尤为重要。

目前，T. NISHI[1]等基于时刻表以乘务员数量最少为目标建立数学模型，并采用列生成技术对问题进行求解；P. ALEFRAGIS等[2]利用改进的启发式拉格朗日松弛法对乘务排班问题进行求解，开发以效率为目标的乘务排班问题优化器；S. JÜTTE等[3]针对乘务排班集覆盖模型提出基于分解思想的列生成算法，在合理时间内得到大规模排班问题优质解；L. P. VEELENTURF等[4]以时序重排方法构建在一定概率扰乱状态下的线性0-1整数规划乘务排班模型，设计以提高时间效率为目标的拉格朗日列生成技术对问题进行求解；R. HANAFI等[5]构建以乘务工作量最小为目标的0-1整数规划模型，采用模拟退火和自构启发混合算法进行求解；余祖俊等[6]对保证轻轨司机双休日的“双齿轮”轮班模型及其均衡算法进行了研究；李献忠等[7]在引用乘务广义费用实现多目标优化的基础上，将实际的城市轨道交通排班优化问题分为日班和夜班两部分解决；李献忠等[8]还以上海城市轨道交通为背景，研究了城市轨道交通排班软件中的优化方法；张增勇等[9]基于惩罚费用构建了乘务排班优化模型，并设计了改进的Dijkstra算法和离散粒子群算法；吴玲玲等[10]建立了基于遗传算法的轨道交通线路排班模型；丰富等[11]将时间均衡度作为给定周期条件下评价乘务员值乘时间与休息时间的合理程度指标，构建了基于该均衡度的乘务排班计划优化模型。但以往研究全部集中在构建数学模型和优化算法生成乘务排班计划方面，主要目的是降低运营成本、平衡乘务工作时间及强度，没有从驾驶过程去探究乘务排班效果。笔者以提高驾驶质量为目标，结合驾驶过程，构建驾驶质量同间休时间、出勤时刻、结束时刻的函数关系，建立数学优化模型，对乘务排班计划进一步优化。

1 问题分析

乘务排班计划最终是以轮乘卡的形式呈现，轮乘卡上规定每个驾驶员一天的出勤次数及一次出勤间休时间、出勤时刻、结束时刻。将一次出勤定义为一个工作单元，这样，乘务排班计划就被划分为若干工作单元。一次出勤效果定义为驾驶质量且由该工作单元的对标精度、准时度、舒适度和能耗度组成，而驾驶质量直接受间休时间、出勤时刻、结束时刻的影响，因此，以提高驾驶质量为目标，构建驾驶质量同间休时间、出勤时刻、结束时刻的函数关系，建立数学优化模型。为方便计算，此处对涉及到的变量进行说明：

1)K表示列车司机集合，|K|>表示司机数量；

2)L表示轮乘卡集合，|L|>表示轮乘卡数量；

3)l表示轮乘卡中工作单元集合，|l|>表示轮乘卡中工作单元数量；

4)li表示第l个轮乘卡中第i个工作单元包含的车站集合，|li|>表示第l个轮乘卡中第i个工作单元包含的车站数量。

2 模型构建

按实际轮乘卡对每个工作单元进行实验，记录间休时间x1、出勤时刻x2、结束时刻x3，最终第k个司机驾驶质量y表示为x1、x2、x3的函数关系，即y=hk(x1,x2,x3)，其中驾驶质量y值由对标精度、准时度、舒适度和能耗度加权平均求得。

2.1 对标精度Q1

(1)

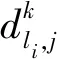
2.2 准时度Q2

(2)

2.3 舒适度Q3

(3)

(4)

式中：h=0,1,2,……,n-1；tj为从j站出发的时间；tj+1表示到达j+1站的时间；v(t)表示从j站到j+1车站的时间-速度函数。

(5)

式中：h=0,1,2,……,n-1。

因此，由式(3)得第l个轮乘卡第i个工作单元的舒适度：

(6)

2.4 能耗度Q4

只讨论牵引能耗，不考虑节能坡影响，假设加速度为正时表示列车处于牵引状态，则第k个司机在第l个轮乘卡第i个工作单元中从j站到j+1车站之间的牵引能耗为

(7)

式中：M表示列车质量；Z表示满足当t∈[zm-1,zm]时，a(t)≥0且a(zm-1)=a(zm)=0，zm-1≥tj，zm≤tj+1的区间个数。

由式(7)得第l个轮乘卡第i个工作单元的能耗度为

(8)

驾驶质量Y值由对标精度、准时度、舒适度和能耗度加权平均求得，即：

(9)

式中：ωi为第i个指标权重。ωi由层次分析法确定[12]。

3 数据拟合

第k个司机驾驶质量同工作单元三要素之间的函数关系式为

y=hk(x1,x2,x3)

(10)

式中：k=1,2,3,……,|K|>。

目前无预估函数模型直接拟合三元函数是非常困难的，但拟合一元函数较容易且准确性较高，所以以拟合低难度函数为基础，采用微分知识推导出hk的函数表达式。推导过程如下：

设f1,f2,f3分别表示x1,x2,x3同y之间的函数关系，即y=f1(x1)，y=f2(x2)，y=f3(x3)。

运用特征线法，设x1,x2,x3，y满足方程H(x1,x2,x3，y)=0得到特征方程组：

解得：hk(x1,x2,x3)=f1(x1)+f2(x2)+f3(x3)+3C4-C1-C2-C3其中C1,C2,C3,C4为常数。

由初始条件hk(0,0,0)=0得：

(11)

目标是在包含{h1,h2,h3,……,h|K|>}的函数空间中，找出h*使其到h1,h2,h3,……,h|K|>的距离之和最小，如式(12)：

(12)

4 实例分析

由于现场实验难度较大，借助广州地铁三号线GZML3综合仿真实训软件系统，该系统仿真程度高，长期用于现场人员培训，实验可信度较高。实验选取广州地铁三号线番禹广场站到天河客运站共16个站(图1)，由67位有驾驶经验的司机严格按照轮乘卡间休时间、出勤时刻和结束时刻进行实验，通过该系统收集每位司机在每个工作单元的对标误差、时间误差、区间v-t曲线数据，根据公式(1)、(2)、(6)、(8)求出司机在工作单元内的对标精度Q1、准时度Q2、舒适度Q3、能耗度Q4,计算得ω1=0.565，ω2=0.262 2，ω3=0.117 5，ω4=0.055 3，再根据公式(9)得出驾驶质量y。

利用1stOpt软件分别对(x1,y)、(x2,y)、(x3,y)数据进行无预估模型最优拟合，结果如表1。

图1 GZML3综合仿真实训软件系统实验线路Fig. 1 The experimental route of comprehensive simulation softwareGZML3

函数函数表达式平均拟合优度出现频次f1(x1)(p1+p2x+p3x2+p4x3+p5x4+p6x5+p7x6)/(p8+p9x+p10x2+p11x3+p12x4+p13x5+p14x6)0.929 846(p1+p3x+p5x2)/(1+p2x+p4x2)0.742 44(p1+p3x0.5+p5x+p7x1.5)/(p1+p2x0.5+p4x+p6x1.5+p8x2)0.846 87f2(x2)1/(p1(x+p2)2+p3)+p40.806 412p1/(p2(x+p3)2+p4)+p50.911 8521/(p1+p2/x2+p3e(-x))0.611 23f3(x3)p1+p2/(1+(x-p3)/p4)20.736 64p1/(p2(x-p3)2+p4)+e-p5x-p6p7()20.910 0461/(p1(x+p2)2+p3)+p40.380 48(p1+p3x+p5x2)/(1+p2x+p4x2)0.896 39

在样本实验中可以观察出明显的规律性，因此选取平均拟合优度高和出现频次多的公式作为f1(x1)、f2(x2)、f3(x3)的函数表达式，则有：

(13)

将式(12)展开得：

(14)

式中：(x1_min,x1_max)、(x1_min,x1_max)、(x1_min,x1_max)分别为x1,x2,x3取值的上下限，根据实验数据可知，x1-min=0，x1-max=7.99，x2-min=0，x2-max=22，x3-min=0，x3-max=23.976 2。将式(13)视为无约束最优化问题，利用1stOpt软件对参数p1,p2,……,p26进行标定，得p1=0.014 36，p2=-1.838 56，p3=0.333 14，p4=-5.726 56，p5=-2.440 93，p6=3.873 13，p7=5.669 24，p8=10.493 18，p9=-5.623 09，p10=8.342 02，p11=2.175 97，p12=-5.076 68，p13=0.258 03，p14=3.749 41，p15=6 704.974 47，p16=-7.911 18，p17=-18.871 22，p18=0.027 80，p19=2.122 8，p20=3.515，p21=-8.78，p22=3.515,p23=2.42，p24=-0.021 9，p25=8.146，p26=1.000 18。

h*确定后将排班方案转化为带约束条件的非线性规划问题，模型如下：

maxy=h*(x1,x2,x3)

式中：U、L分别为驾驶持续时间的上下限，这里分别取2、5。

以该带约束条件的非线性规划问题对实际工作中可能遇到的七种情况分别进行讨论。

情况一：对间休时间x1、出勤时刻x2、结束时刻x3进行决策，当x1=0.658 7，x2=18.930 5，x3=20.948 0时，驾驶质量最大。

情况二：固定间休时间x1且x1∈[x1_min,x1_max]，对出勤时刻x2、结束时刻x3进行决策，使(x1,x2,x3)对应最大驾驶质量，如图2。

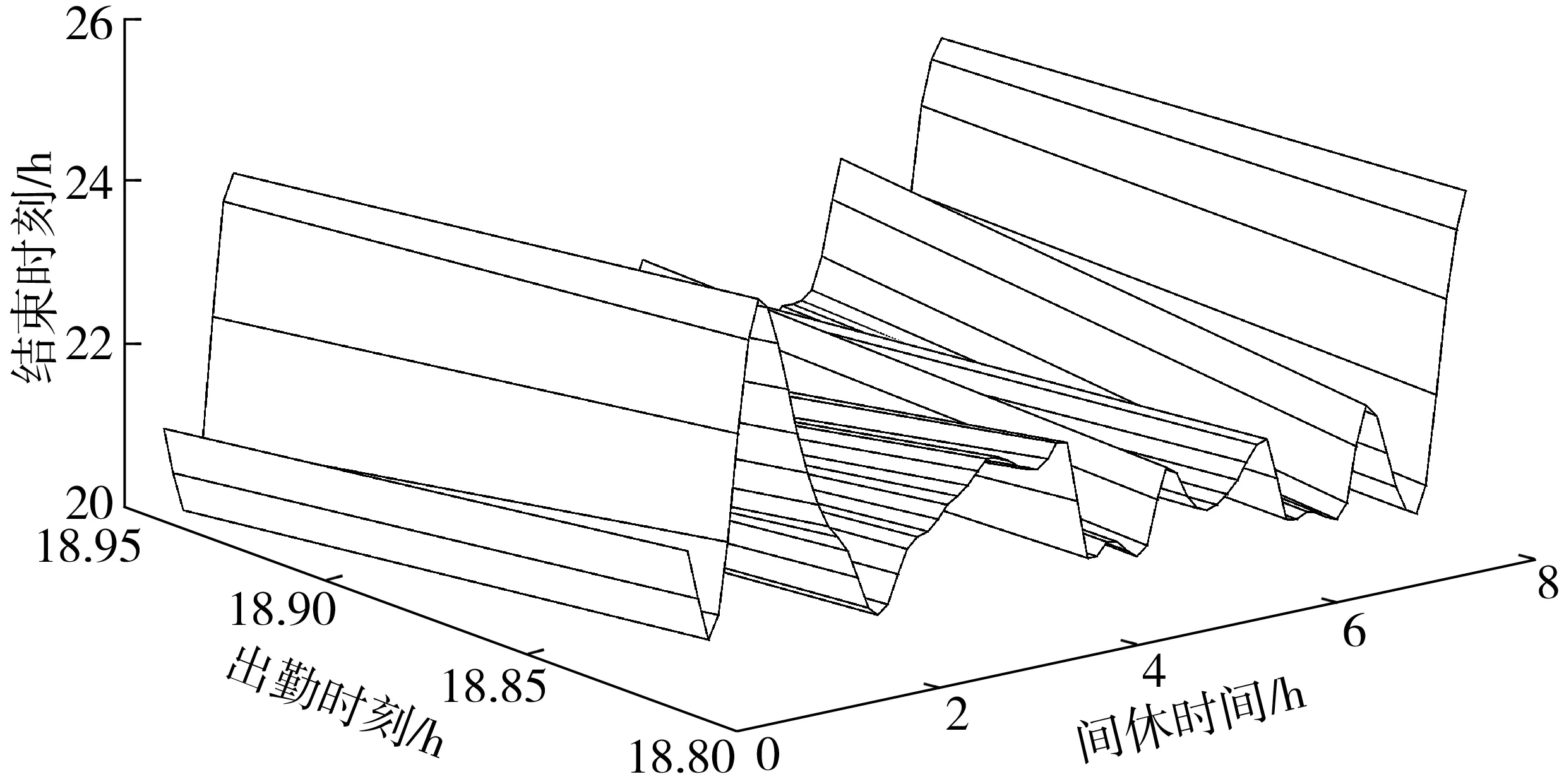
图2 固定间休时间Fig. 2 Fixed rest time

情况三：固定出勤时刻x2且x2∈[x2_min,x2_max]，需对间休时间x1、结束时刻x3进行决策，使当x2取某值时，对应的x1、x3的取值能使驾驶质量最大，如图3。

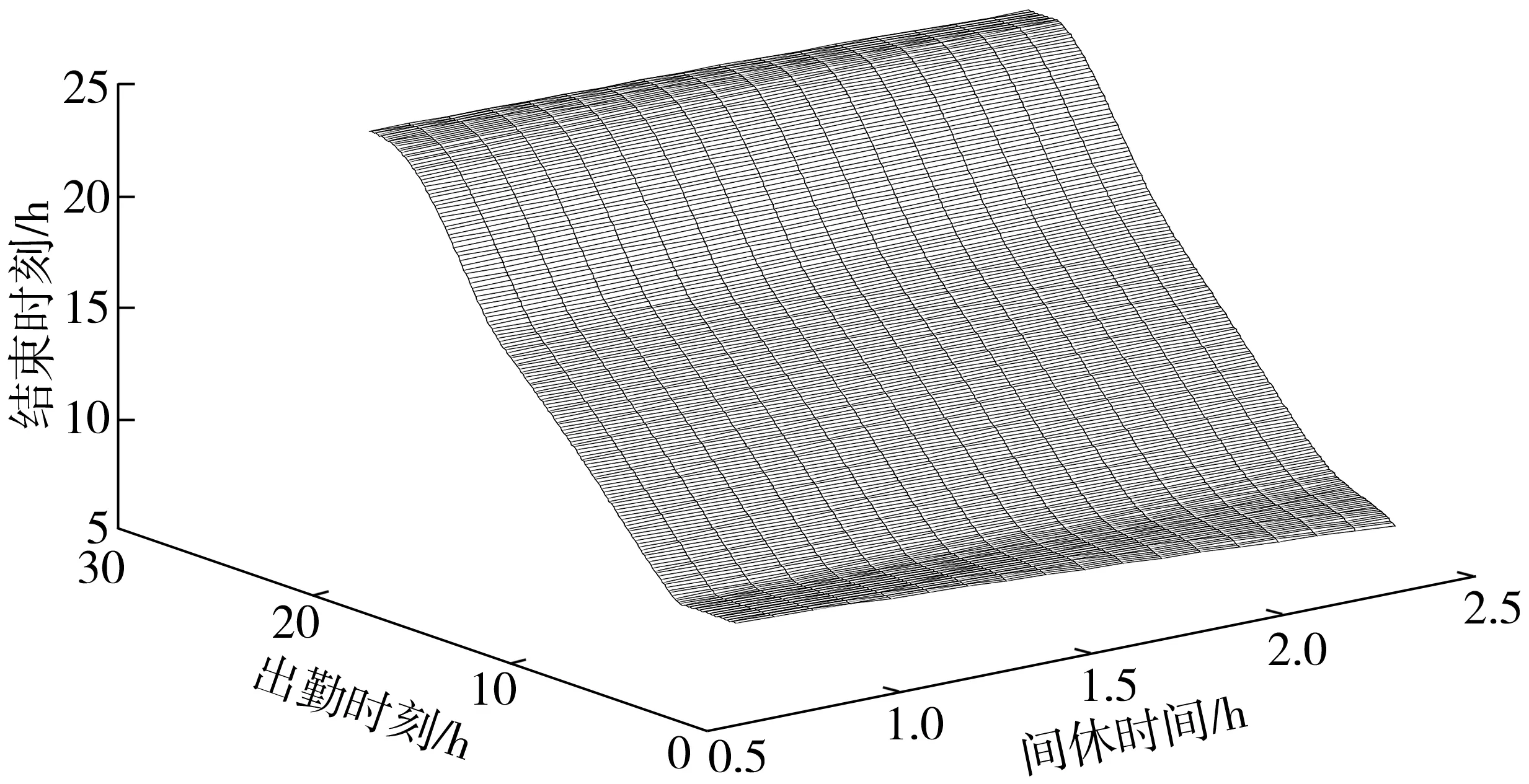
图3 固定出勤时刻Fig. 3 Fixed attendance time

情况四：固定结束时刻x3且x3∈[x3_min,x3_max]，需对间休时间x1、出勤时刻x2进行决策，使当x3取某值时，对应的x1、x2的取值能使驾驶质量最大，如图4。

情况五：固定间休时间x1且x1∈[x1_min,x1_max]，固定出勤时刻x2且x2∈[x2_min,x2_max]，需对结束时刻x3进行决策，使当x1、x2取某值时，对应的x3的取值能使驾驶质量最大，如图5。

图5 固定间休时间、出勤时刻Fig. 5 Fix rest time, attendance time

情况六：固定间休时间x1且x1∈[x1_min,x1_max]，固定结束时刻x3且x3∈[x3_min,x3_max]，需对出勤时刻x2进行决策，使当x1、x3取某值时，对应的x2的取值能使驾驶质量最大，如图6。

图6 固定间休时间、结束时刻Fig. 6 Fixed interval rest time, end moment

情况七：固定出勤时刻x2且x2∈[x2_min,x2_max]，固定结束时刻x3且x3∈[x3_min,x3_max]，需对间休时间x1进行决策，使当x2、x3取某值时，对应的x1的取值能使驾驶质量最大，如图7。

图7 固定出勤时间、结束时刻Fig. 7 Fixed interval rest time, end moment

为了验证模型的有效性，需进行对比试验。根据模型重新确定七种情况下x1、x2、x3的最优取值，在相同实验样本、实验设备和实验条件下按最优值再次进行实验，将实验结果与原结果对比，如图8～图14。结果表明优化后平均驾驶质量分别提高14.09%、8.17%、6.41%、9.45%、6.31%、7.64%、7.57%。

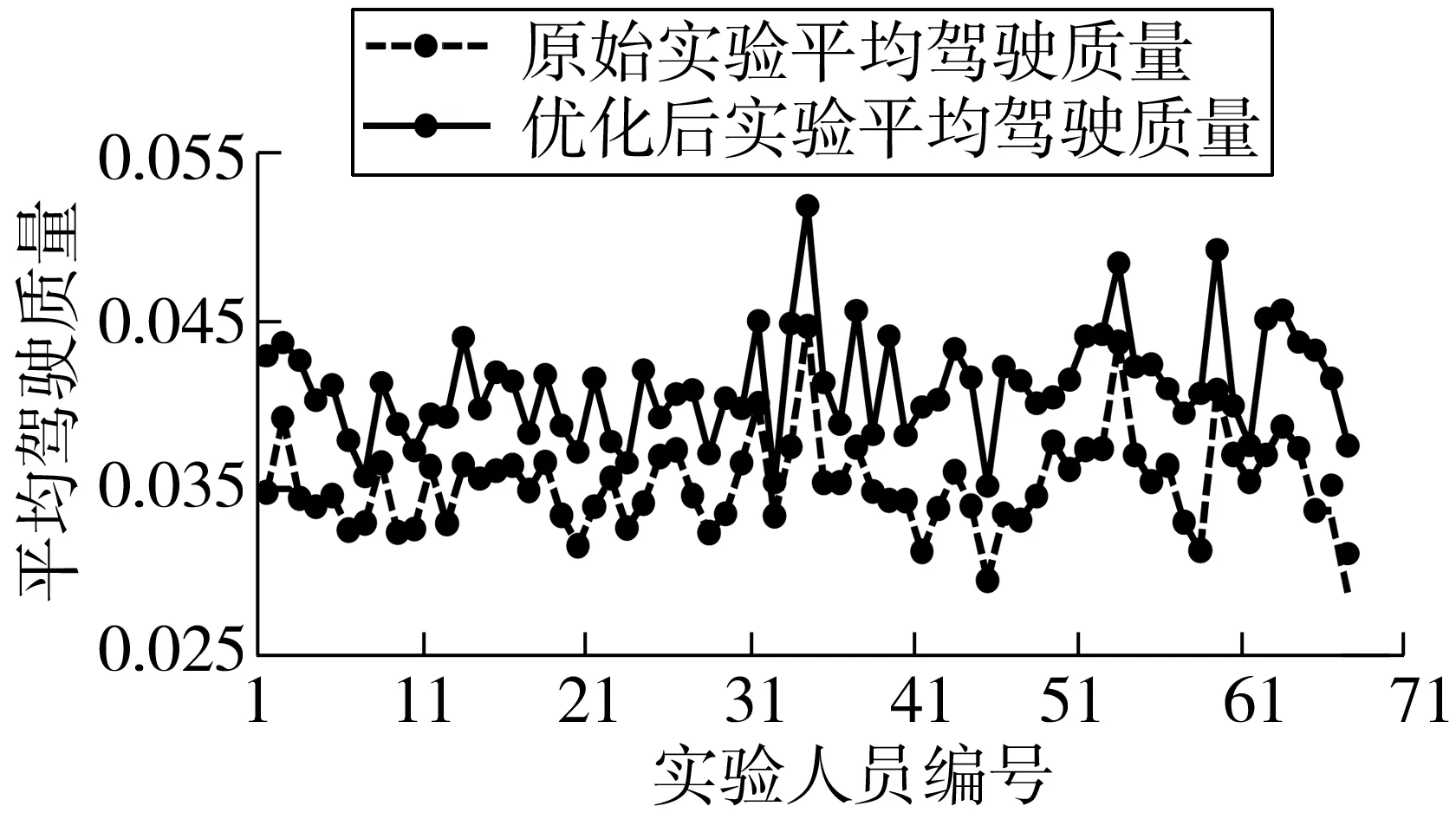
图8 情况一下平均驾驶质量对比Fig. 8 Contrast chart of average steering qualityunder case 1

图9 情况二下平均驾驶质量对比Fig. 9 Contrast chart of average steering qualityunder case 2

图10 情况三下平均驾驶质量对比Fig. 10 Contrast chart of average steering quality under case 3

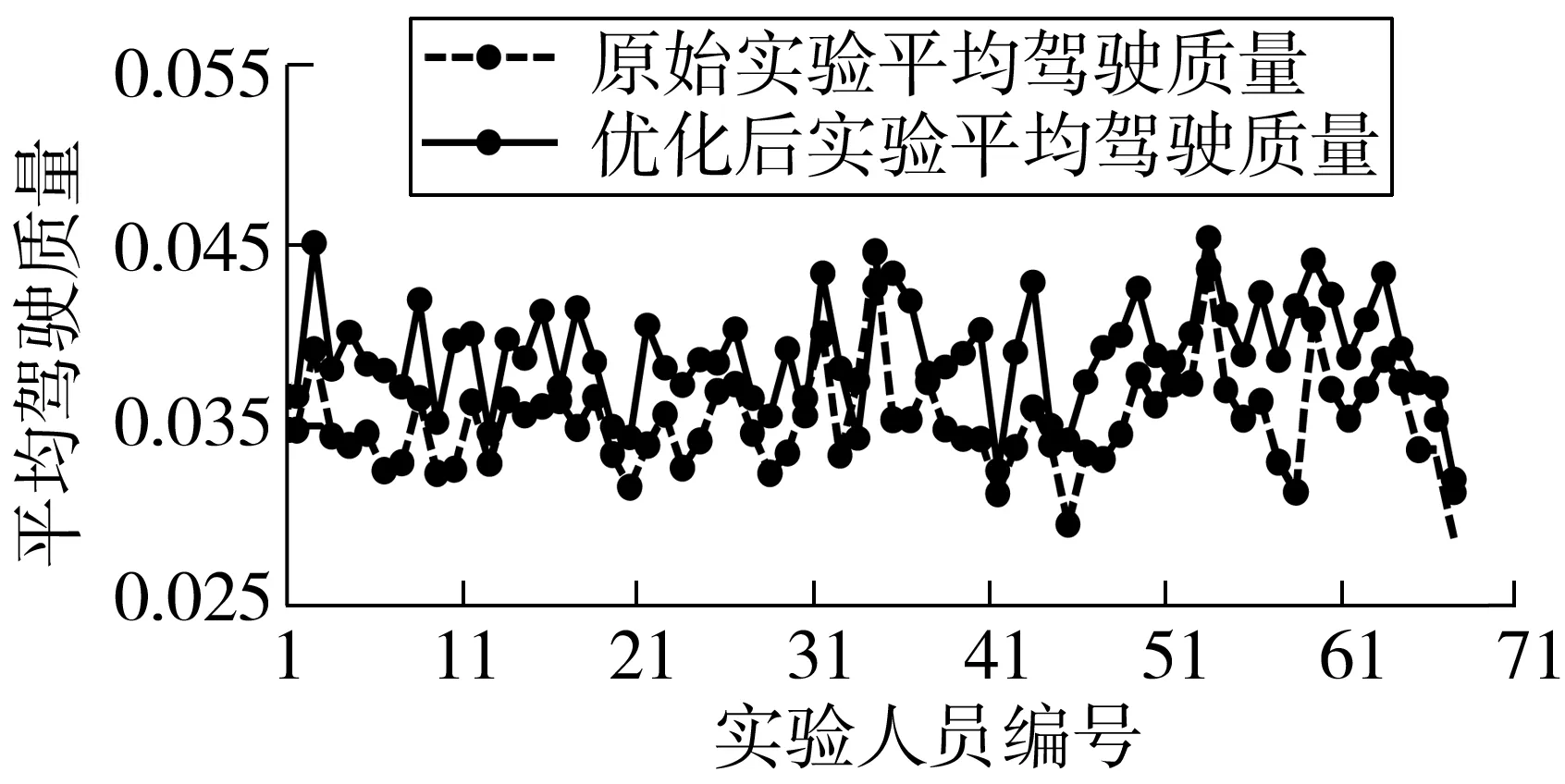
图11 情况四下平均驾驶质量对比Fig. 11 Contrast chart of average steering quality under case 4

图12 情况五下平均驾驶质量对比Fig. 12 Contrast chart of average steering quality under case 5

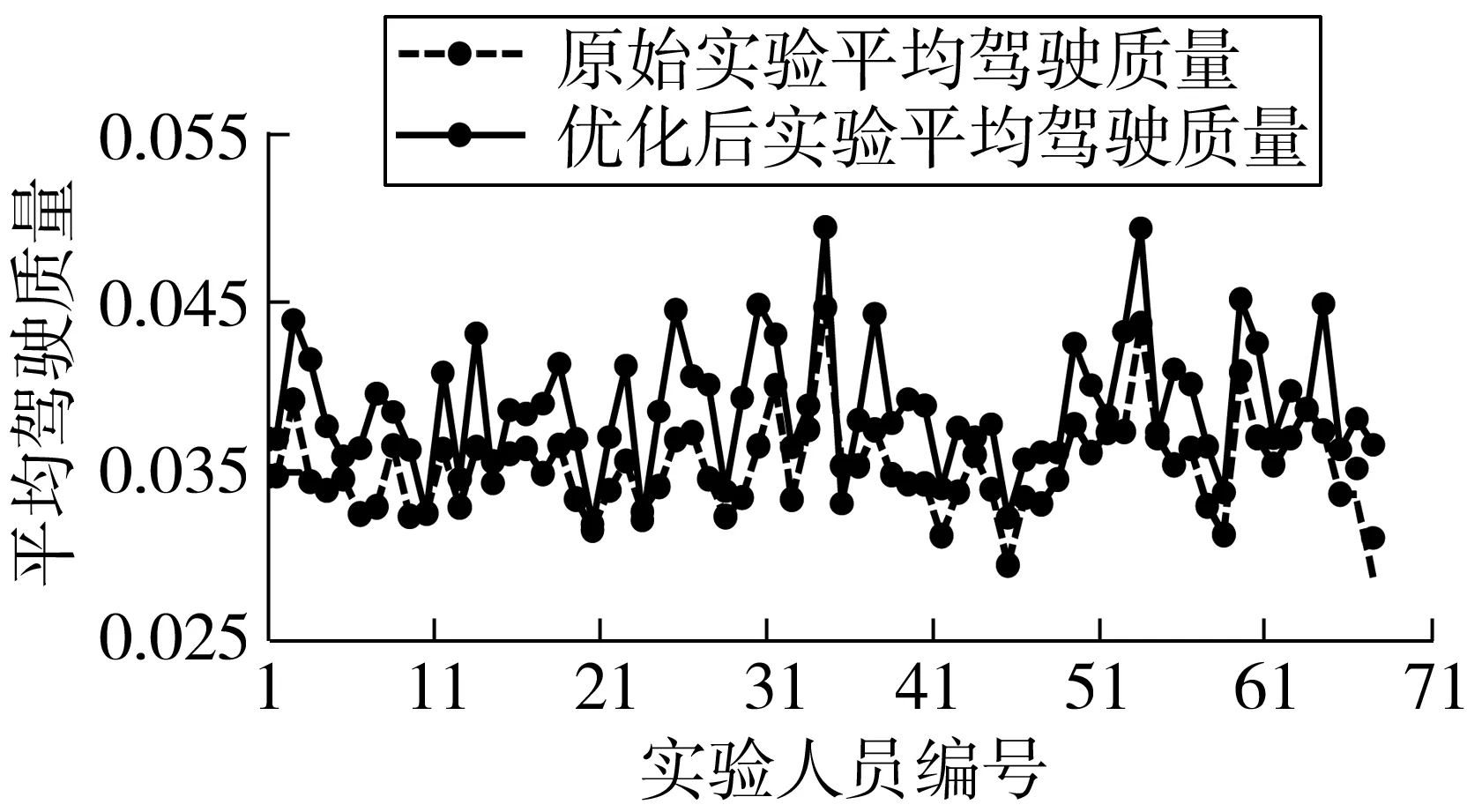
图13 情况六下平均驾驶质量对比Fig. 13 Contrast chart of average steering quality under case 6

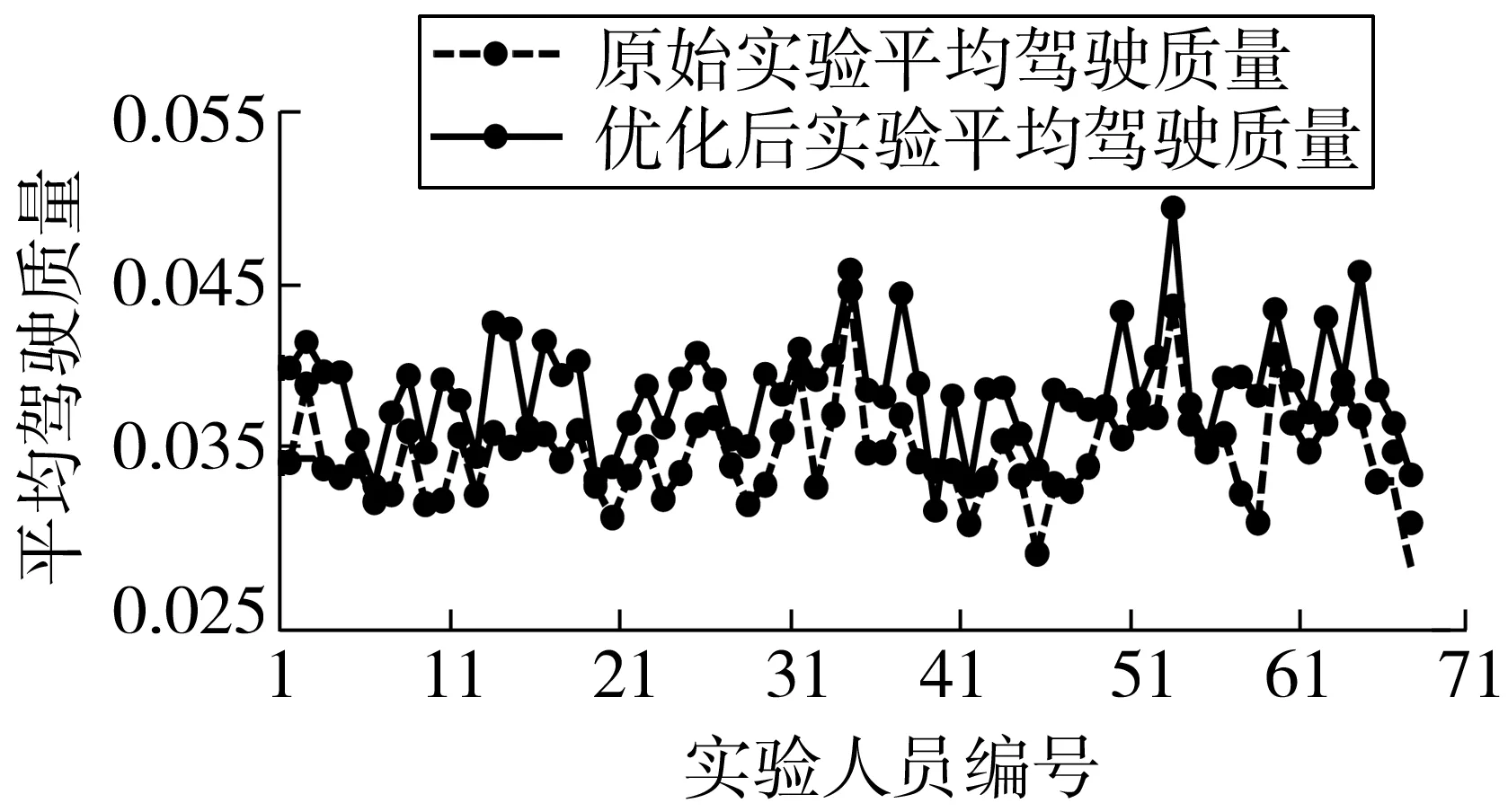
图14 情况七下平均驾驶质量对比Fig. 14 Contrast chart of average steering quality under case 7

5 结 语

将已有乘务排班计划和驾驶过程结合，通过推导计算得到驾驶质量同间休时间、出勤时刻、结束时刻的函数关系，构建约束非线性规划模型，对乘务排班计划进行优化，用优化结果设计对比实验，结果表明在间休时间、出勤时刻、结束时刻不同优化组合条件下驾驶质量有明显提高，说明笔者构建的模型能有效优化乘务排班计划。

在高精度仿真系统上进行的模拟实验，与真实环境有一定出入；另外，各城市采用的车辆、信号系统、通信系统等环境不同，都会对实验结果造成影响。因此，对不同环境下的测试有待进一步探讨。