转子辅助槽对IPM性能的影响研究

安治国，刘高朋，高 尉

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

近年来随着世界各国对环境保护越来越重视以及化石燃料逐渐枯竭 ，由于电动汽车的“油井-车轮”(WTW)效率高于内燃机汽车。纯电动汽车的应用将减少毒物的来源，大大降低对臭氧层的破坏，也是减少温室气体的重要途径[1-3],电动汽车成为世界未来汽车发展的重要方向，因此需要开发性能优异的驱动电机以满足电动汽车要求。

国内外学者对齿槽转矩的影响因素及解决方法进行了研究，研究了电枢齿的形状、斜槽、极数和槽数配合对齿槽转矩的影响[4]，取得了大量的研究成果。文献[5-6]中，对齿槽转矩的解析表达式进行了推导并由此提出了一系列削弱齿槽转矩的方法，包括：极槽配合、斜极、斜槽、不等极弧因数组合、不等槽口宽、开辅助槽等，取得了良好的效果；黄克峰等[7]研究了针对圆筒型永磁直线电机存在齿槽力的问题，先得出了气隙磁场强度的解析公式，再依据该解析公式采用能量法推导出了齿槽力解析公式；翟秀果等[8]研究永磁体极弧系数对电机定子绕组感应电势和电机漏磁系数的影响, 并比较3种电机的感应电势THD值和基波值以及漏磁系数的区别。

研究转子外径开辅助槽对永磁同步电机齿槽转矩和感应电动势谐波的影响。利用ANSYS Maxwell软件分析了8极内嵌式永磁同步电机转子辅助槽3种结构参数变化对齿槽转矩的影响[9]，得出空载稳态下仿真不同辅助槽形状对感应电势THD值的影响，以及对空载漏磁系数的影响。

1 瞬态磁场分析理论

瞬态磁场分析可以求解电压、电流激励源为非正弦情况，或者模型中存在运动状态的情况。瞬态磁场求解器中矢量磁位A满足的场方程如式(1)：

(1)

式中：HC为永磁体的矫顽力；v为运动物体的速度；A为矢量磁位；Js为源电流密度。

Maxwell 2D进行瞬态分析时使用一个参考框架，固定在模型某一部分时速度为0。运动物体固定在自身的坐标系，偏时间导数变成全时间导数，因为运动方程为

(2)

因此，矢量磁位在每时间段有限元模型中每点都可获得。

2 电机基本参数

8极内嵌式永磁同步电机的具体参数如表1。

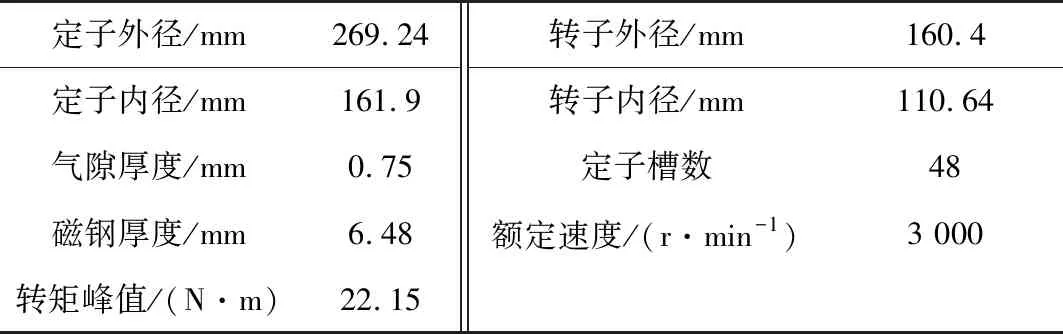
表1 永磁同步电机参数 Table 1 Parameters of permanent magnet synchronous motor

为了节省软件仿真计算时间，给出电机的 1/8模型，如图1，其中转子主要由转子铁心、永磁体和隔磁桥三部分构成。

3 辅助槽结构参数对齿槽转矩的影响

在Maxwell 2D下建立电机瞬态求解器模型，计算开路状态下定子绕组的齿槽转矩波形。

3.1 辅助槽位置对齿槽转矩的影响

保持辅助槽深度值H=2 mm和宽度W=2 mm，设置辅助槽位置θ为变量参考，变化范围从0°～16°，计算步长为4°，对电机模型进行参数化分析。各角度下的齿槽转矩曲峰值曲线如图2。由图2可以看出，当θ=12°时有最小齿槽转矩，峰值达到15.47 N·m，比θ=0°时减小了32.7%。θ=16°时有最大齿槽转矩，峰值达到36.77 N·m。

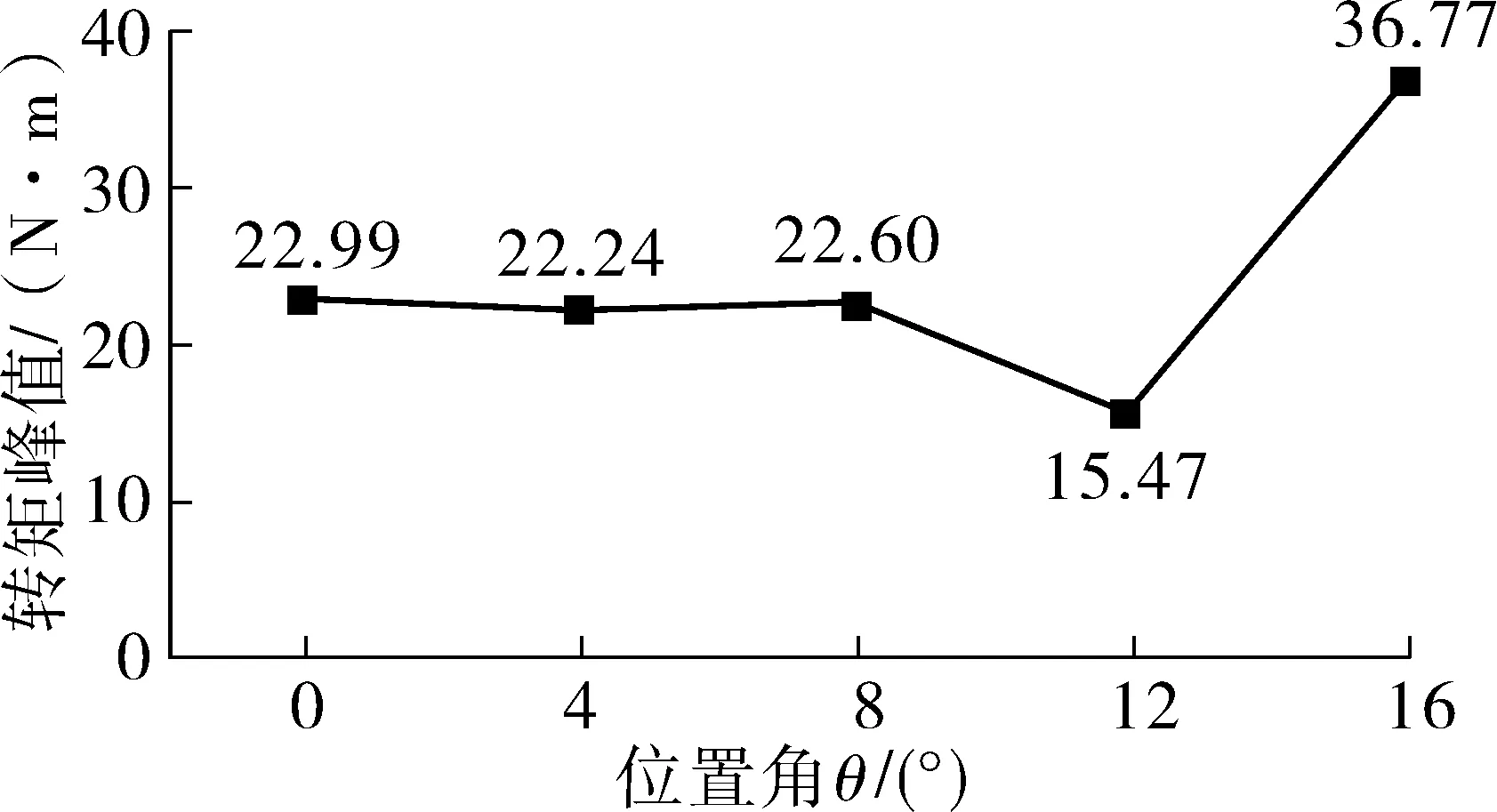
图2 角度θ变化时齿槽转矩峰值变化曲线Fig. 2 Variation curve of cogging torque peak value when angle θchanges

3.2 辅助槽深度对感应电势的影响

保持辅助槽宽度值W=2 mm和位置θ=12°，设置辅助槽宽度H为变量参考，变化范围从0～3 mm，计算步长为0.5 mm，对模型进行参数化分析。各深度下的齿槽转矩峰值曲线如图3。

如图3可以看出，齿槽转矩峰值随辅助槽深度增大先减小再增大，H=1 mm时峰值最小为12.41 N·m，比H=0 mm时减小了45.3%。

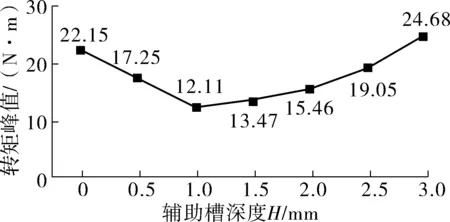
图3 深度H变化时齿槽转矩峰值变化曲线Fig. 3 Cogging torque curve when height H changes

3.3 辅助槽宽度对感应电势的影响

保持辅助槽深度值H=1 mm和角度θ=12°，设置辅助槽宽度W为变量参考，变化范围从0.5～4 mm，计算步长为0.5 mm，对模型进行参数化分析。各宽度下的齿槽转矩峰值曲线如图4。如图4可以看出，W为3.5 mm取得最小峰值为9.42 N·m，相比W=0.5 mm减小了46.3%。齿槽转矩峰值随辅助槽宽度的增大先减小再增大。

图4 宽度W变化时齿槽转矩峰值变化曲线Fig. 4 Cogging torque curve when width W changes

3.4 辅助槽两个结构参数的关联研究

由图2可知，为了达到最优参数设计选择最优角度θ=12°时，进行深度H和宽度W两因素参数化分析，研究其对齿槽转矩的影响，得出在宽度W=3.5 mm、深度H=1 mm时有最小齿槽转矩峰值9.42 N·m，相对于初始设计值减小了57.5%。根据图5、图6，与W方向比较，H方向曲线较陡，H等高线密度明显高于沿W移动的密度，说明此时深度H对峰值的影响较深度H为显著。

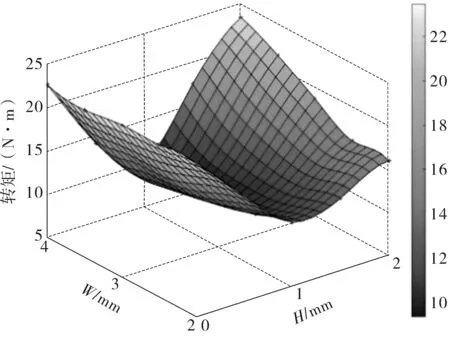
图5 结构参数与齿槽转矩峰值曲面图Fig. 5 Surface map of structural parameters and cogging torque peak value

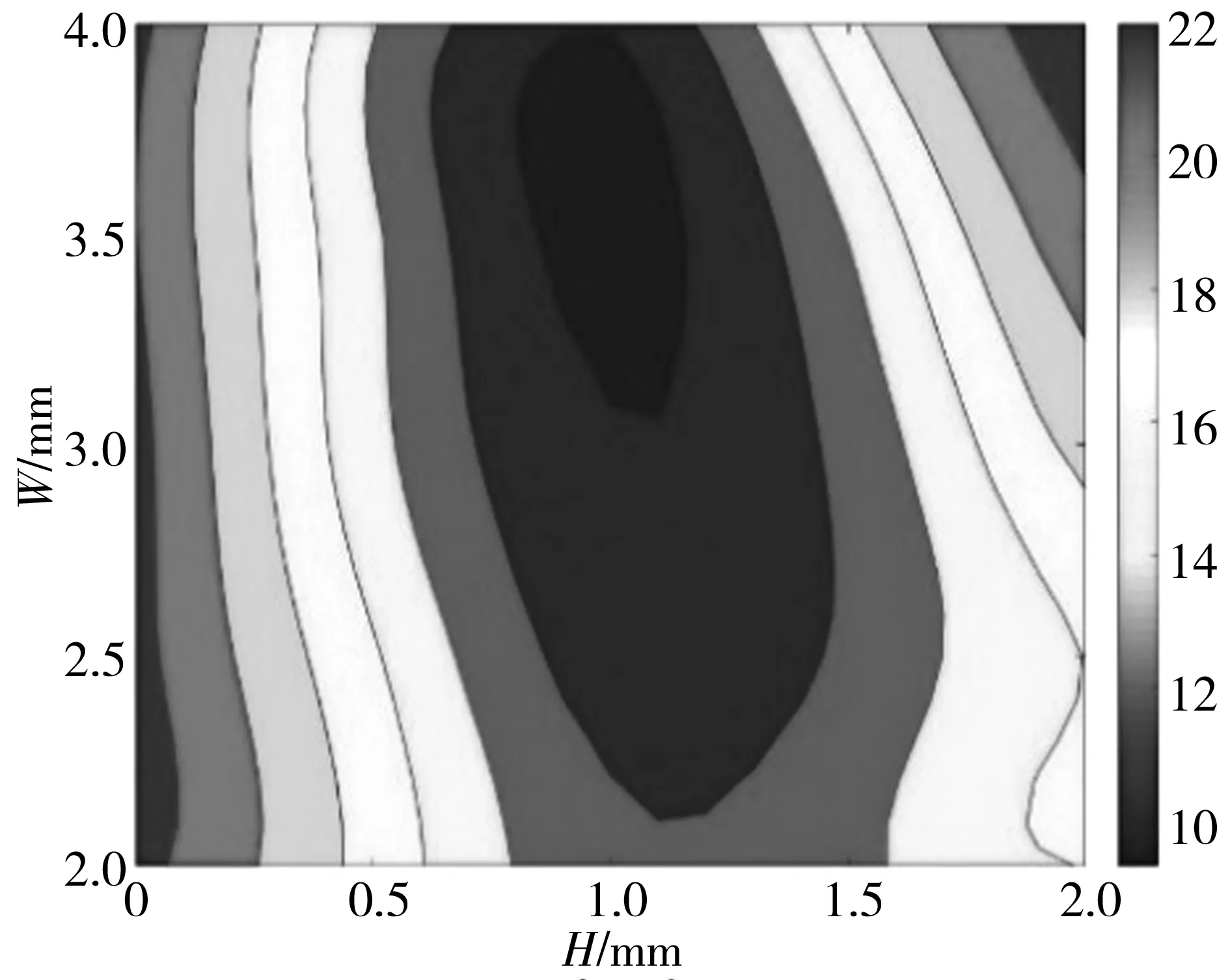
图6 齿槽转矩峰值等高线Fig. 6 Contour map of cogging torque peak value

4 辅助槽参数对电机感应电动势的影响

在Maxwell 2D下建立电机瞬态求解器模型，计算开路状态下定子绕组的感应电动势。1988年G.BERTOTTI在STERINMETZ的研究基础上发现磁滞损耗与磁场的频率成正比，与磁场的幅值的平方成正比；涡流损耗与磁场幅值及磁场频率的平方成正比；杂散损耗则与磁场幅值及磁场频率的1.5次方成正比[10]。感应电动势对电机铁芯损耗影响较大。

4.1 辅助槽位置对感应电动势的影响

保持辅助槽深度值H=2 mm和宽度W=2 mm，设置辅助槽位置θ为变量参考，变化范围从0°～16°，计算步长为4°，对电机模型进行参数化分析，得到感应电动势曲线如图7。然后对各角度下感应电动势进行傅立叶分析，获得如图8频谱图，由图可知，当θ=12°时，第11次谐波显著降低。

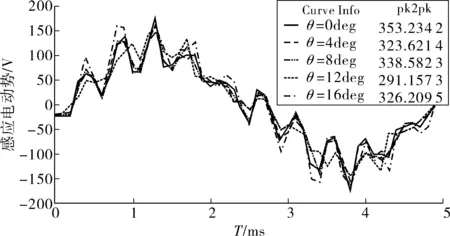
图7 θ变化时A相感应电势曲线Fig. 7 Induced electromotive force curve in phase A when θ changes

4.2 辅助槽深度对感应电动势的影响

保持辅助槽宽度值W=2 mm和位置θ=12°，设置辅助槽深度H为变量参考，变化范围从0～3 mm，计算步长为0.5 mm，对模型进行参数化分析，得到感应电动势曲线如图9。对感应电动势进行傅立叶分析，获得各阶次谐波如图10，基波值随深度增加略微增加，第11次谐波随深度增加显著降低。

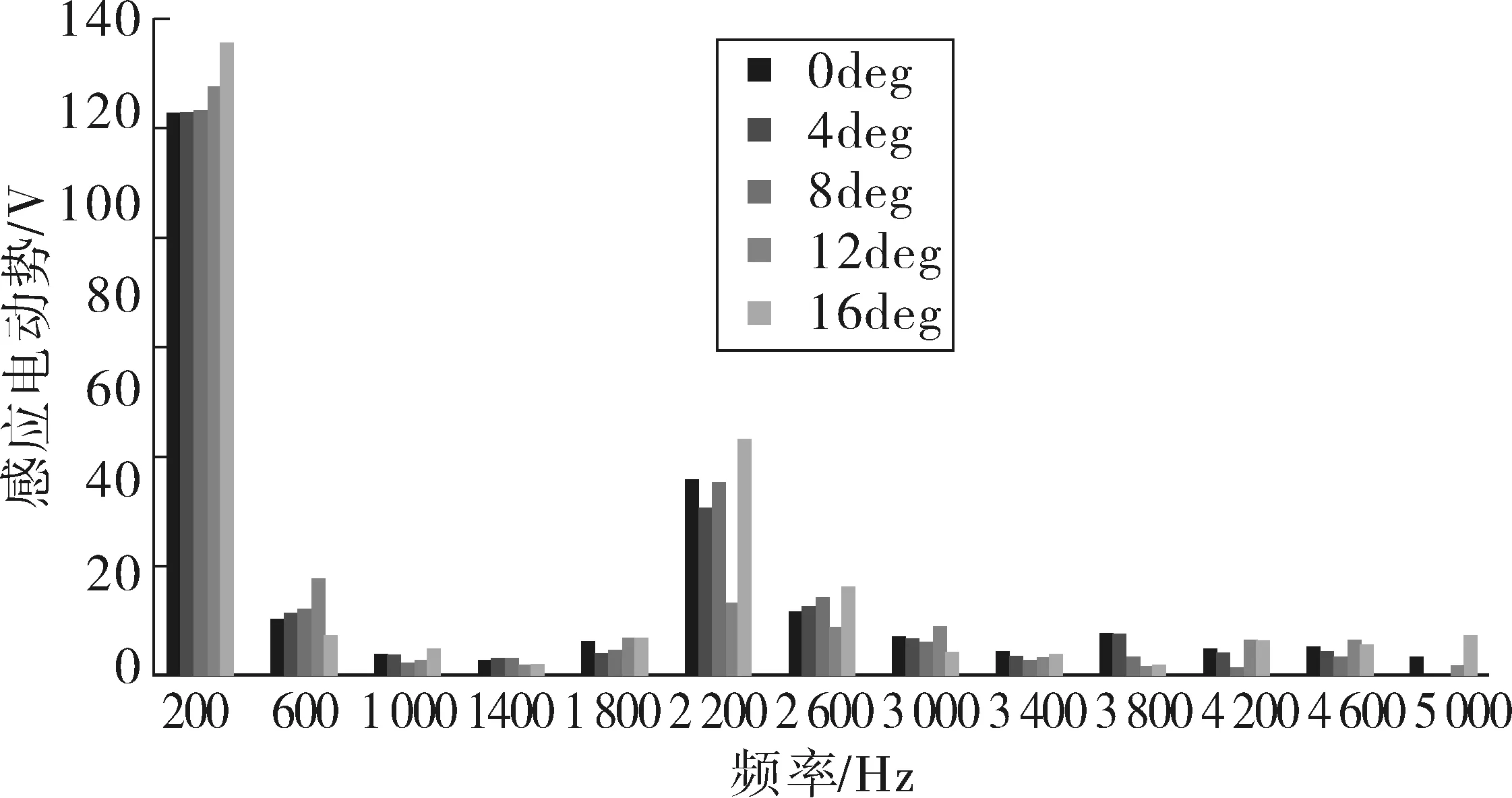
图8 角度θ变化时感应电动势谐波频谱Fig. 8 Harmonic spectrogram of induced electromotive force whenθ changes

4.3 辅助槽宽度对感应电动势的影响

保持辅助槽深度值H=1 mm和角度θ=12°，设置辅助槽宽度W为变量参考，变化范围从0.5～4 mm，计算步长为0.5 mm，对模型进行参数化分析，得到感应电势曲线如图11。对感应电动势进行傅立叶分析，获得各阶次谐波如图12，基波幅值随宽度增加略微增加，第11次谐波幅值随宽度增加而显著降低。

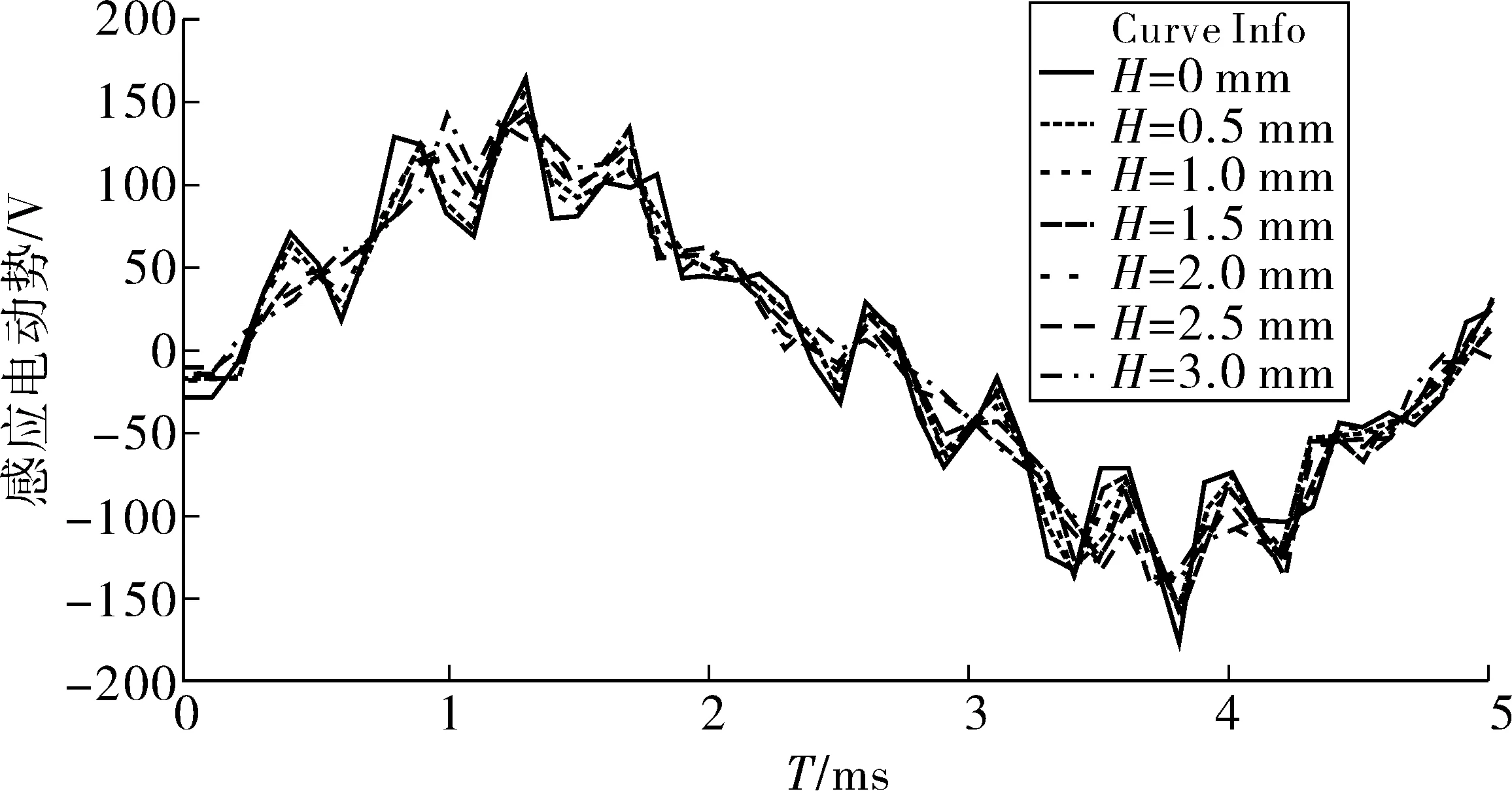
图9 H变化时A相感应电势曲线Fig. 9 Induced electromotive force curve in phase A when H changes

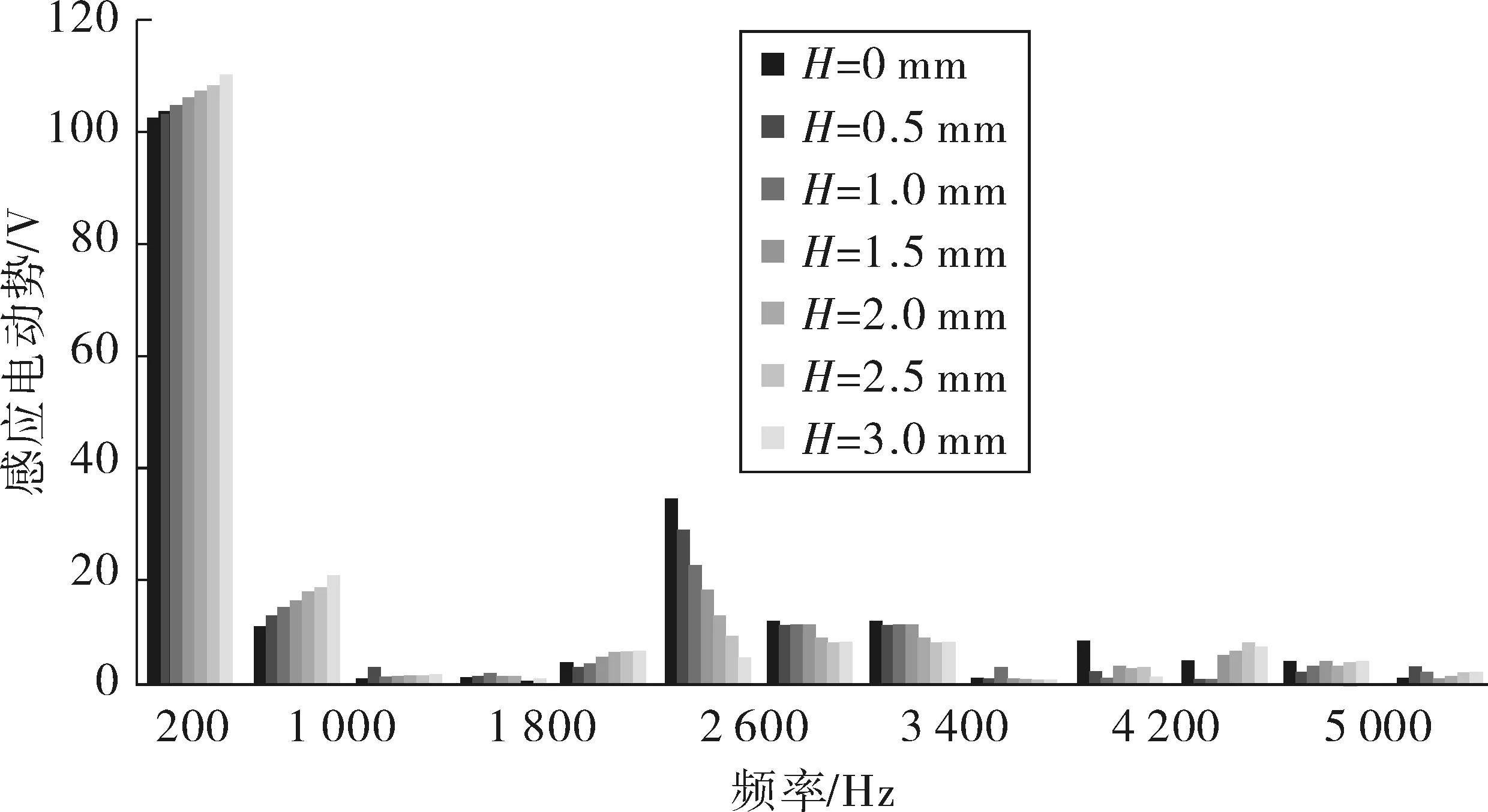
图10 深度H变化时感应电动势谐波频谱Fig. 10 Harmonic spectrogram of induced electromotive force whenheight H changes

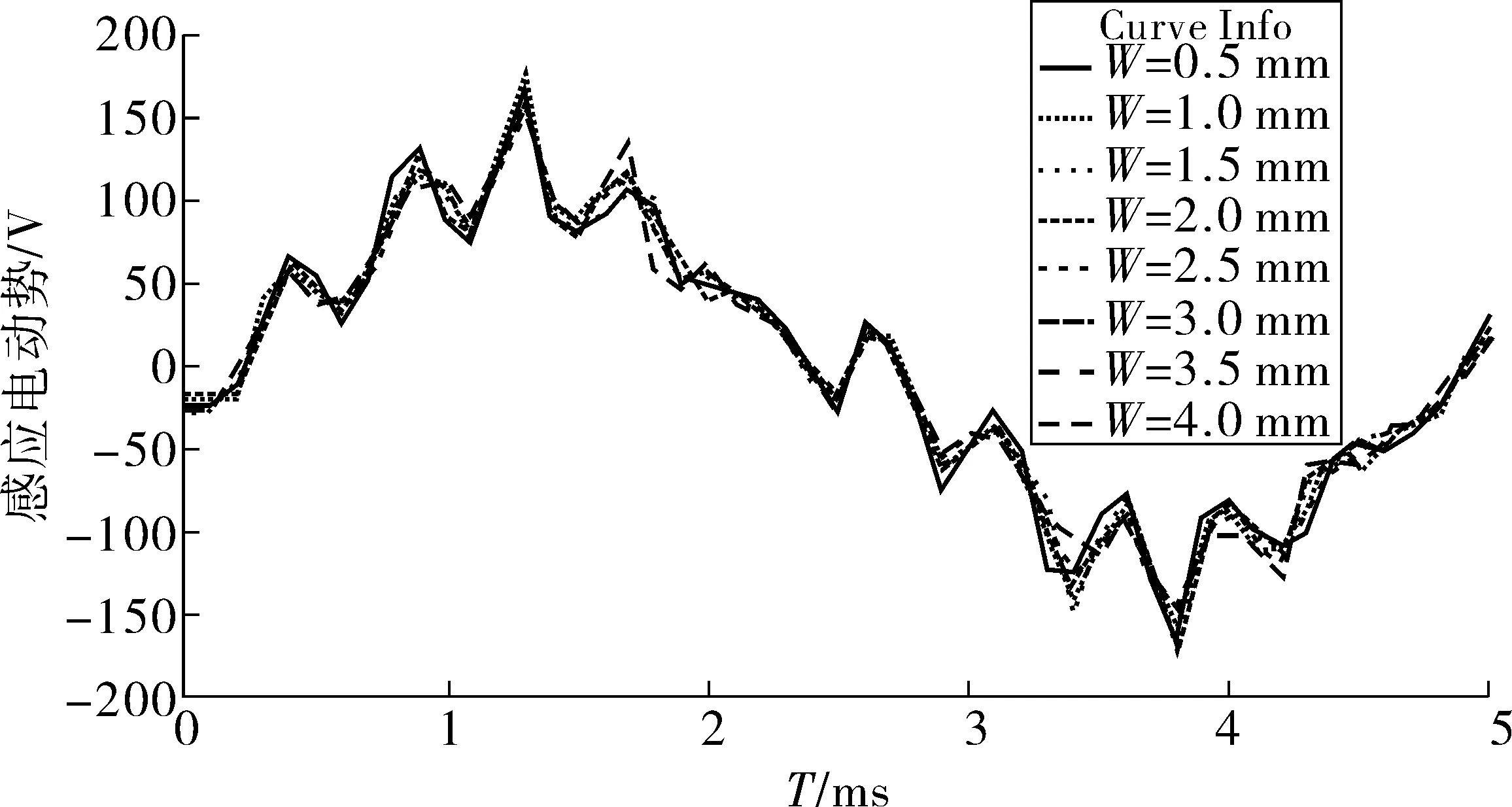
图11 宽度W变化时A相感应电势曲线Fig. 11 Induced electromotive force curve in phase A when width Wchanges

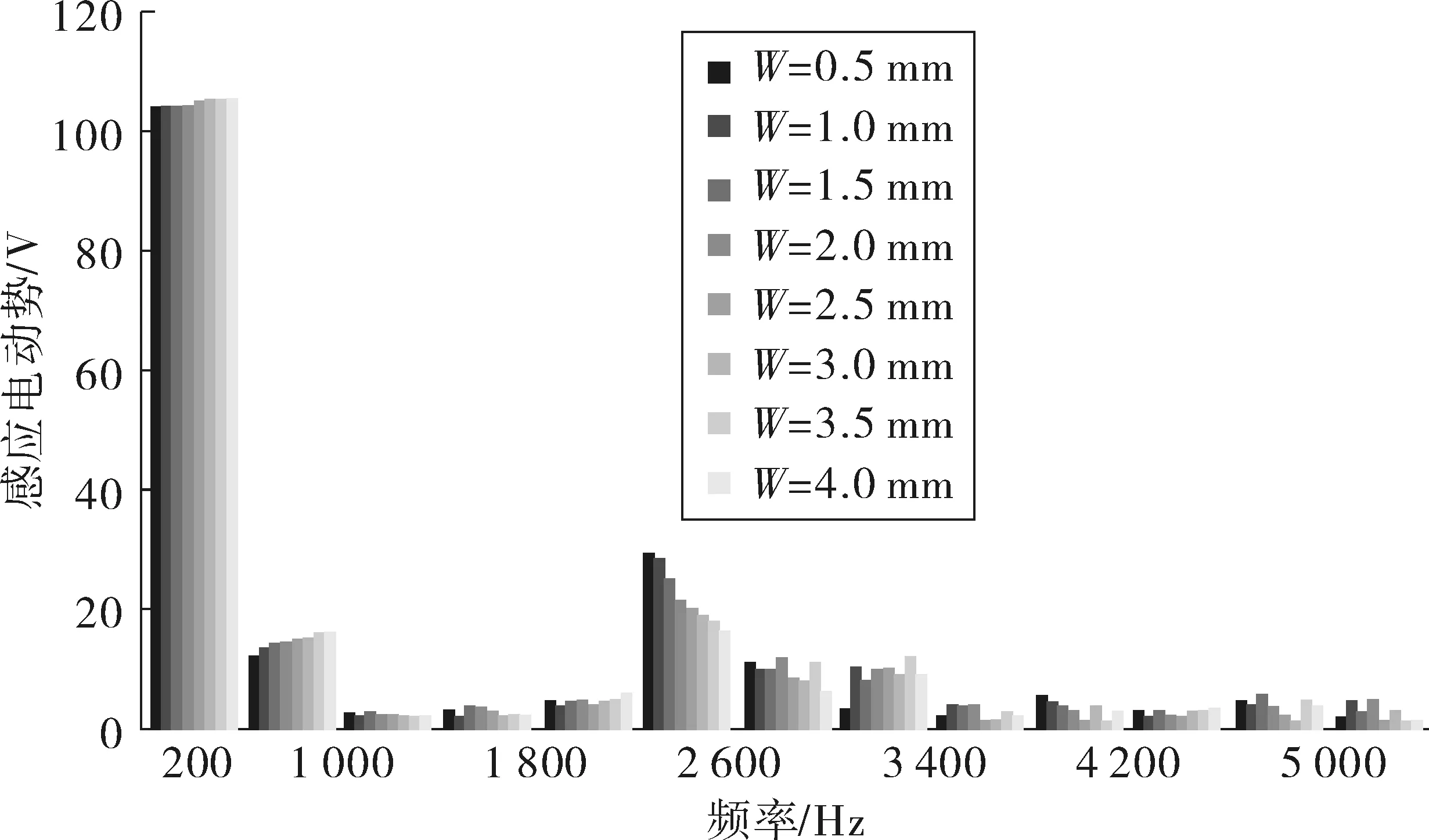
图12 宽度W变化时感应电动势谐波频谱Fig. 12 Harmonic spectrogram of induced electromotive force whenW changes

5 辅助槽结构对电机漏磁系数的影响

永磁同步电机的空载漏磁系数σ=φm/φδ，其中φm为永磁体向外部磁路提供的总磁通，φδ为通过气隙与定子绕组交链的主磁通，空载漏磁包括极间漏磁和端部漏磁[4-5],研究转子铁心辅助槽形状对电机漏磁系数的影响，对电机具有重要意义。选取图1永磁同步电机模型， 利用Maxwell 2D 静态场求解器，仿真最有辅助槽结构参数下电机的磁力线Flux_lines等势图。

由图13可知，永磁体向外部磁路匝链的磁力线有91根，通过气隙与定子绕组交链的磁力线有54根，则此时永磁同步电机的空载漏磁系数σ=1.685。由图14可知，永磁体向外部磁路匝链的磁力线有91根，通过气隙与定子绕组交链的磁力线有52根，则无辅助槽时永磁同步电机的空载漏磁系数σ=1.75。辅助槽可以对漏磁系数产生影响，空载漏磁系数降低3.71%，提高永磁材料的利用程度和抗去磁能力。

6 结 论

通过对8级内嵌式永磁同步电机转子辅助槽3种参数对齿槽转矩峰值、感应电动势以及漏磁系数影响的研究，得出以下结论：

1)在辅助槽宽度W=3.5 mm，角度θ=12°，深度H=1 mm时有最小齿槽转矩峰值为9.42 N·m。

2)当辅助槽位置θ=12°时，第11次谐波显著降低；第11次谐波随深度H和宽度W的增加而降低。

3)辅助槽可以对漏磁系数产生影响，降低永磁同步电机的空载漏磁系数，提高永磁材料的利用程度和抗去磁能力。